远场距离除了10λ和2D^2/λ还有别的吗？

Posted 2023-04-04 无线认证x英利检测

远场距离始终是OTA测试中让大家头疼的一个因素。上一篇我们讨论了关于TRP的测试，为什么可以不用远场距离而使用更小的测试距离。但对于EIRP或其他方向性的测试项，却只能使用远场距离来进行。关于远场距离，我们曾经发过一篇文章，远场距离是10λ还是2D^2/λ，最近又有了一些新的发现，与大家分享。

01

—

远场距离还可以有哪些

先来回顾一下之前的主要内容：远场距离被认为是10倍波长的距离，这一考虑是从“源天线和测试天线之间相互耦合的影响”角度出发考虑的。当间距大于约10个波长时，这种影响可以忽略不计。根据对距离天线10个波长的极短偶极子天线进行的计算，电感场（inductive field）的电平（也就是反应场中会耦合的部分）将比辐射场的电平低36dB。一般对于较小的天线（电气尺寸在一个波长以下），远场距离R可以用10λ来近似表示。

而2D^2/λ的远场距离，是从“相位变化随测试天线口径的影响”角度去考虑的。发射天线辐射的电磁波的波前是一个球面，如果 AUT 与发射天线的距离不够远，AUT的相位分布容易产生较大的误差，根据IEEE规定的天线测量误差标准， 要求最大相位误差不大于 π/8，也就是22.5度。由此而推算出2D^2 /λ可以近似为相位误差符合要求的远场距离标准。

那是不是远场距离就一定是10λ，或者是2D^2/λ了呢？看起来并不是，远场距离的确定可以有不同的规则。我们在CTIA终端OTA测试标准《Test Plan for Wireless Device Over-the-Air Performance》中看到了不同频段的最小测试距离的规定如下表所示：

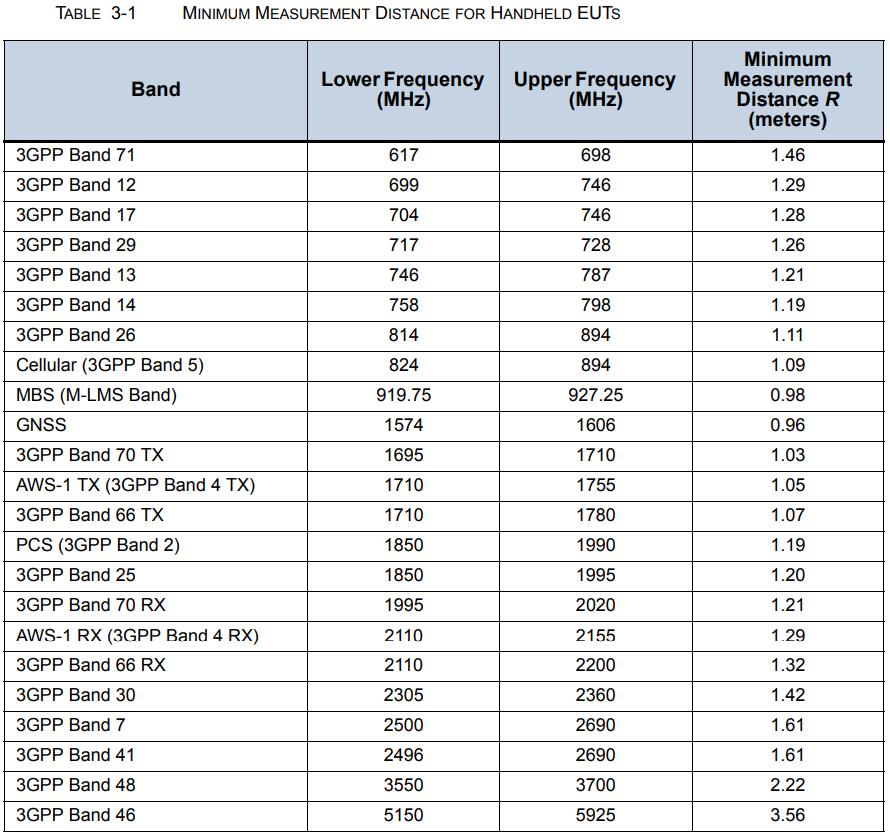
这个Minimum Measurement Distance R（最小测试距离）是如何得出的？

它有三种远场距离的计算规则，并选择了每个频段中最严格的距离做为最终远场测试距离。

• 规则一：需大于2D^2/λ（相位不确定性限值）；
• 规则二：需大于3D（振幅不确定性限值）；
• 规则三：需大于3λ（反应性近场限值）；

其中D是EUT的尺寸，λ是所在频段的自由空间波长。对于自由空间测试，D只是EUT的最大尺寸，但对于头/手模型测试，头/手模型必须包括在D中。在CTIA标准中，D被选为头/手模型的那部分尺寸，它在确定EUT的TRP或TIS时起着重要作用，并定义D=300毫米。

if D=300 mm；
Freq < 1GHz, 反应性近场限值3λ为最大远场距离；
Freq > 1.5GHz, 相位不确定性限值2D^2/λ为最大远场距离；
1GHz < Freq < 1.5GHz, 振幅不确定性限值3D为最大远场距离；

所以算来算去，得到下表：

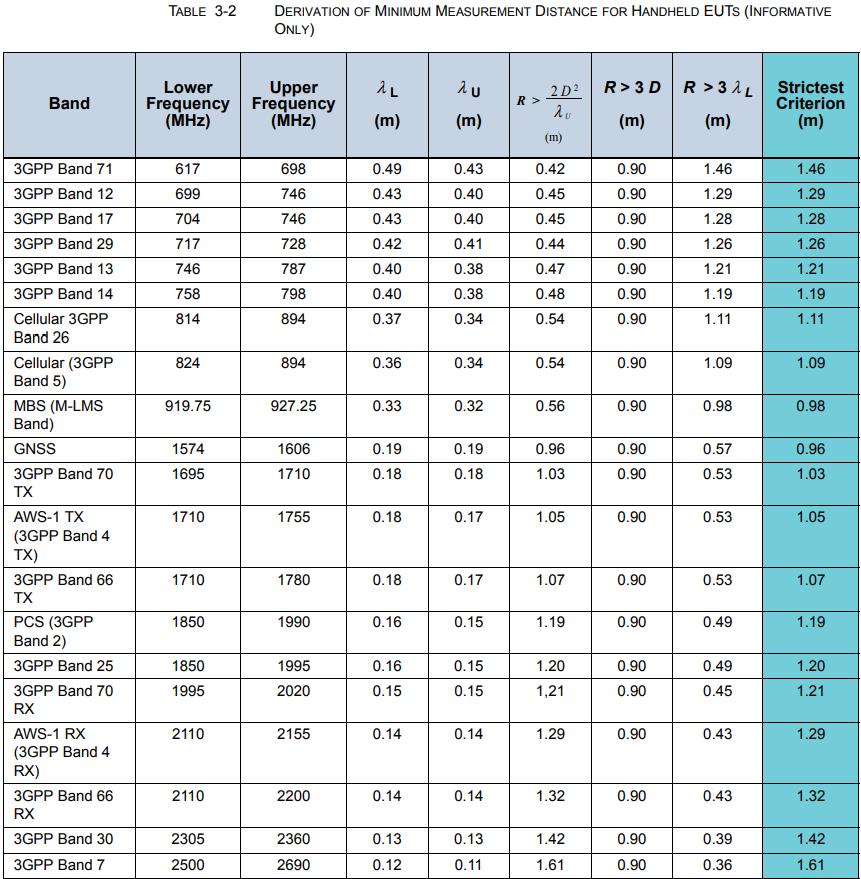
频率f的升高和D的增大，都会让2D^2/λ越来越大，因为：

2D^2/λ = 2D^2 × f/c = 2D^2 × f(Hz)/(3×10^8)；

02

—

远场距离规则选择

看来远场距离，是可以根据所需的测试而进行选择的，CTIA之所以可以选择最严格的规则作为远场距离，一是想对终端OTA测试环境的执行准则进行严格统一管理，二是因为针对目前的蜂窝网络，频率还不是太高，被测终端的尺寸还不是太大，最严格的远场距离在成本与尺寸方面也基本可行。

但如果是汽车的OTA测试，例如在5.9GHz频段，如果按照整个汽车的尺寸，比如D=6米计算，使用规则一，即2D^2/λ，远场距离大概是1416米，这实在是无法想象。即使不按照整车，只按照天线尺寸，比如D=1米计算，也需要大概40米的远场距离。

如果测试并不关心相位的不确定性（相位变化的影响是零陷点的幅度以及旁瓣的幅度值发生变化），大可不必非得使用2D^2/λ来计算远场距离。根据上述经验，3λ-10λ，或者3D等，都可以成为远场测试的距离。

以上信息由英利检测（Teslab）整理发布，欢迎一起讨论，我们一直在关注这方面的发展，如有引用也请注明出处。

国家高新技术企业；唯一覆盖中国和欧美运营商认证服务机构；业内最为优秀第三方认证服务商之一；专业的人做专业的事；

入库：┆移动┆联通┆电信┆中国广电┆

欧美：┆GCF┆PTCRB┆VzW┆ATT┆TMO┆FCC┆

中国：┆CCC┆SRRC┆CTA┆

号码：┆IMEI┆MAC┆MEID┆EAN┆

Lambda演算归约！归约！归约！

（一）

这里先不列出λ项的正式定义，只记住λ表达式语义上的构造方式为：

1. x

一个单独的变量名是一个λ项表达式；

2. (λx.M)

该λ表示一个函数。其中 M 是这个函数的函数体，M 本身也是一个 λ项。

除了 x 之外，M 中可能还有其他变量名，λ 这个符号用于指示函数体 M 的参数为 x。

了便于理解，可以将 M 看作函数体，x 看作形参，即变量名。

 

例如：λx.x+3 即表示一个函数 f(x) = x+3，该函数会返回x与3相加的结果

要注意的是，我这里的写法并不规范，在λ表达式中，二元运算符是作为前缀的。x+3 应该写作 (+ x 3)。所以这个表达式的正规写法是 λx.(+ x 3)。至于为什么，我们之后再讲。

3. (M N)

其中 M，N 均为λ项表达式。

如果 M 本身是一个函数，我们说将函数 M 应用于 N。如果 M 不是函数，不接受参数，N 将在求值的过程中被忽略。

例如：（λx.(+ x 3) 4），其中M为表达式 λx.x+3，N 为 4。这个表达式表示将函数应用于 4，即f(4) 

 

所以一个典型的λ表达式具有如下形式：

 (λx.M) N，为了方便去掉括号写作 λx.M N

 

其中 M 是函数体，x 可以看作形参，即变量名， N 可以看作实参，即变量值。

 

函数本身也可以作为参数，例如（λx.x）（λx.(+x 3)),  表达式左边就是一个函数，这个函数将返回它自己的参数，将这个函数应用于我们之前说的函数 f，参数是 f，那么这个函数将返回 f。

 

如此一来，第一种形式的λ表达式代表一个变量；

第二种表达式代表一个函数；

第三种表达式则代表将函数应用于一个值，即一次函数调用。

 

（二）归约

第一种表达式的值即它本身；

第二种表达式的值表示这个函数本身；

因此，在讨论求值时，我们只关心第三种，即将一个函数应用于另一个λ表达式时，如何计算它的值。

 

如上所述，λ表达式的应用等效于一次函数调用。我们知道，调用函数的时候，会将所有的形参替换用实参的值，并返回计算结果。因此，我们说在表达式 λx.M N 中，函数体 M 里的 x 与表达式 N 绑定，M 中剩下未绑定的变量则是自由变量。

 

对 λx.M N 进行求值时，M 中所有的 x 都将被替换为 N。这一过程称为归约，归约后得到简化的λ表达式，可以进一步归约直至无法再归约，此时的表达式就是对原表达式进行求值的结果。

 

考虑一个函数 f(x)=x+3，写作λ表达式就是 (λx.(+x 3))。

如前所述，当我们想计算 f(4) 时，将函数应用于 4，表达式为 λx.(+ x 3) 4。

按照归约的法则，函数体 (+ x 3) 中的 x 被 4 替换，函数表达式变为 (+ 4 3)，结果为 7。

 

考虑另一个函数 g(y)=y*2，λ表达式 λy.(* y 2)。

如果我们想将函数 g 应用于 f(4) 的计算结果，即 g(f(4))，我们可以将 g 的λ表达式应用于上述表达式，即 λy.(* y 2)  (λx.(+ x 3) 4)

 

然后我们进行归约，这里有两种归约顺序。

 

一种是同之前一样，先计算右边表达式的值，即归约为 λy.(* y 2) 7。

然后将函数体 (* y 2) 中的 y 替换为 7，得到 (* 7 2)。

最终结果是 14。

 

另一种归约顺序是先计算最外层的应用，即将y替换为右边的表达式(λx.(+ x 3) 4)，得到归约后的表达式(* (λx.(+ x 3) 4) 2)。

再归约内层的应用，替换 x 得到 (* (+ 4 3) 2)。

最终结果为(* 7 2)=14。

 

在这个例子中，不同的归约顺序得出了相同的结果，然而，这并不是普遍现象。这里面暗藏了一个计算机程序中常见的概念：作用域。