K-Means聚类若干问题

Posted 2023-04-04

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了K-Means聚类若干问题相关的知识，希望对你有一定的参考价值。

参考技术A 1 K-Means聚类收敛性怎么证明？一定会收敛？？？

2 聚类中止条件：迭代次数、簇中心变化率、最小平方误差MSE？？？

3 聚类初值的选择，对聚类结果的影响？？？（K-Means对初值是敏感的）

4 肘部选择法——确定聚类数K

没有所谓最好的选择聚类数的方法，通常是需要根据不同的问题，人工进行选择的。选择的时候思考我们运用 K-均值算法聚类的动机是什么，然后选择能最好服务于该目的标聚类数。当人们在讨论，选择聚类数目的方法时，有一个可能会谈及的方法叫作“肘部法则”。关于“肘部法则”，我们所需要做的是改变 K 值，也就是聚类类别数目的总数。我们用一个聚类来运行 K 均值聚类方法。这就意味着，所有的数据都会分到一个聚类里，然后计算成本函数J，K 代表聚类种类。

我们可能会得到一条类似于这样的曲线。像一个人的肘部。这就是“肘部法则”所做的，让我们来看这样一个图，看起来就好像有一个很清楚的肘在那儿。好像人的手臂，如果你伸出你的胳膊，那么这就是你的肩关节、肘关节、手。这就是“肘部法则”。你会发现这种模式，它的畸变值会迅速下降，从 1 到 2，从 2 到 3 之后，你会在 3 的时候达到一个肘点。在此之后，畸变值就下降的非常慢，看起来就像使用 3 个聚类来进行聚类是正确的，这是因为那个点是曲线的肘点，畸变值下降得很快，K 等于 3 之后就下降得很慢，那么我们就选 K 等于 3。当你应用“肘部法则”的时候，如果你得到了一个像上面这样的图，那么这将是一种用来选择聚类个数的合理方法。

uk是第k 个类的重心位置。成本函数是各个类畸变程度（distortions）之和。每个类的畸变程度等于该类重心与其内部成员位置距离的平方和。若类内部的成员彼此间越紧凑则类的畸变程度越小，反之，若类内部的成员彼此间越分散则类的畸变程度越大。求解成本函数最小化的参数就是一个重复配置每个类包含的观测值，并不断移动类重心的过程。

importnumpyasnpimportmatplotlib.pyplotaspltfromsklearn.clusterimportKMeansfromscipy.spatial.distanceimportcdistx = np.array([1,2,3,1,5,6,5,5,6,7,8,9,7,9])y = np.array([1,3,2,2,8,6,7,6,7,1,2,1,1,3])data = np.array(list(zip(x, y)))# 肘部法则求解最佳分类数# K-Means参数的最优解也是以成本函数最小化为目标# 成本函数是各个类畸变程度（distortions）之和。每个类的畸变程度等于该类重心与其内部成员位置距离的平方和# 画肘部图aa=[]K = range(1,10)forkinrange(1,10): kmeans=KMeans(n_clusters=k) kmeans.fit(data) aa.append(sum(np.min(cdist(data, kmeans.cluster_centers_,'euclidean'),axis=1))/data.shape[0])plt.figure()plt.plot(np.array(K), aa,'bx-')plt.show()# 绘制散点图及聚类结果中心点plt.figure()plt.axis([0,10,0,10])plt.grid(True)plt.plot(x, y,'k.')kmeans = KMeans(n_clusters=3)kmeans.fit(data)plt.plot(kmeans.cluster_centers_[:,0], kmeans.cluster_centers_[:,1],'r.')plt.show()

5 K-Means优缺点及适用范围

K值需要预先给定，属于预先知识，很多情况下K值的估计是非常困难的，对于像计算全部微信用户的交往圈这样的场景就完全的没办法用K-Means进行。对于可以确定K值不会太大但不明确精确的K值的场景，可以进行迭代运算，然后找出Cost Function最小时所对应的K值，这个值往往能较好的描述有多少个簇类。

K-Means算法对初始选取的聚类中心点是敏感的，不同的随机种子点得到的聚类结果完全不同

K-Means算法并不是适用所有的样本类型。它不能处理非球形簇、不同尺寸和不同密度的簇。

K-Means算法对离群点的数据进行聚类时，K均值也有问题，这种情况下，离群点检测和删除有很大的帮助。（异常值对聚类中心影响很大，需要离群点检测和剔除）

5.K-Means算法对噪声和离群点敏感，最重要是结果不一定是全局最优，只能保证局部最优。

6 从K-Means 到 Gaussian Mixture Model

数据表示

在 k-means 中，我们用单个点来对 cluster 进行建模，这实际上是一种最简化的数据建模形式。这种用点来对 cluster 进行建模实际上就已经假设了各 cluster 的数据是呈圆形（或者高维球形）分布的。但在实际生活中，很少能有这种情况。所以在 GMM 中，我们使用一种更加一般的数据表示，也就是高斯分布。

数据先验

在 k-means 中，我们假设各个 cluster 的先验概率是一样的，但是各个 cluster 的数据量可能是不均匀的。举个例子，cluster A 中包含了10000个样本，cluster B 中只包含了100个。那么对于一个新的样本，在不考虑其与 A B cluster 相似度的情况，其属于 cluster A 的概率肯定是要大于 cluster B的。在 GMM 中，同样对数据先验进行了建模。

相似度衡量

在 k-means 中，我们通常采用欧氏距离来衡量样本与各个 cluster 的相似度。这种距离实际上假设了数据的各个维度对于相似度的衡量作用是一样的。但在 GMM 中，相似度的衡量使用的是后验概率

通过引入协方差矩阵，我们就可以对各维度数据的不同重要性进行建模。

数据分配

在 k-means 中，各个样本点只属于与其相似度最高的那个cluster ，这实际上是一种 hard clustering 。在 GMM 中则使用的是后验概率来对各个cluster 按比例分配，是一种 fuzzy clustering 。

Hierarchical Clustering 与 K-Means 和 GMM 这一派系的聚类算法不太相同：

K-Means 与 GMM 更像是一种 top-down 的思想，它们首先要解决的问题是，确定 cluster 数量，也就是 k 的取值。在确定了 k 后，再来进行数据的聚类。

Hierarchical Clustering 则是一种 bottom-up 的形式，先有数据，然后通过不断选取最相似的数据进行聚类。

K-Means业界用得多的原因之一就是收敛快，现在还能通过分布式计算加速，别的原因有调参就一个K。

链接：https://www.jianshu.com/p/cc74c124c00b

来源：

聚类算法K-均值聚类(K-Means)算法

走过路过不要错过

在数据挖掘中，聚类是一个很重要的概念。传统的聚类分析计算方法主要有如下几种：划分方法、层次方法、基于密度的方法、基于网格的方法、基于模型的方法等。其中K-Means算法是划分方法中的一个经典的算法。

一、K-均值聚类(K-Means)概述

1、聚类：

“类”指的是具有相似性的集合，聚类是指将数据集划分为若干类，使得各个类之内的数据最为相似，而各个类之间的数据相似度差别尽可能的大。聚类分析就是以相似性为基础，在一个聚类中的模式之间比不在同一个聚类中的模式之间具有更多的相似性。对数据集进行聚类划分，属于无监督学习。

2、K-Means：

K-Means算法是一种简单的迭代型聚类算法，采用距离作为相似性指标，从而发现给定数据集中的K个类，且每个类的中心是根据类中所有数值的均值得到的，每个类的中心用聚类中心来描述。对于给定的一个（包含n个一维以及一维以上的数据点的）数据集X以及要得到的类别数量K，选取欧式距离作为相似度指标，聚类目标实施的个类的聚类平反和最小，即最小化：

结合最小二乘法和拉格朗日原理，聚类中心为对应类别中各数据点的平均值，同时为了使算法收敛，在迭代的过程中，应使得最终的聚类中心尽可能的不变。

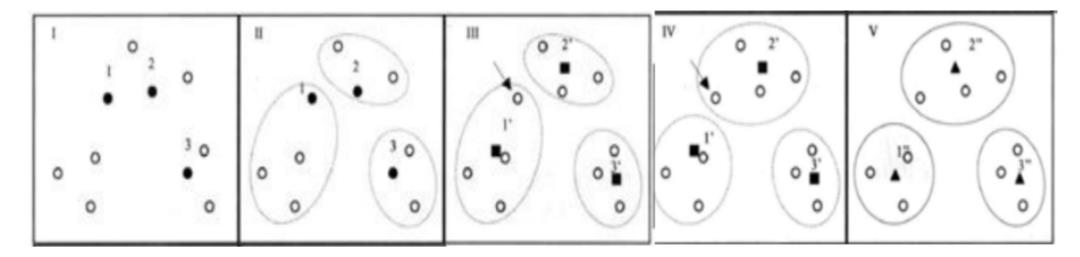
3、K-Means算法流程：

随机选取K个样本作为聚类中心；
计算各样本与各个聚类中心的距离；
将各样本回归于与之距离最近的聚类中心；
求各个类的样本的均值，作为新的聚类中心；
判定：若类中心不再发生变动或者达到迭代次数，算法结束，否则回到第二步。

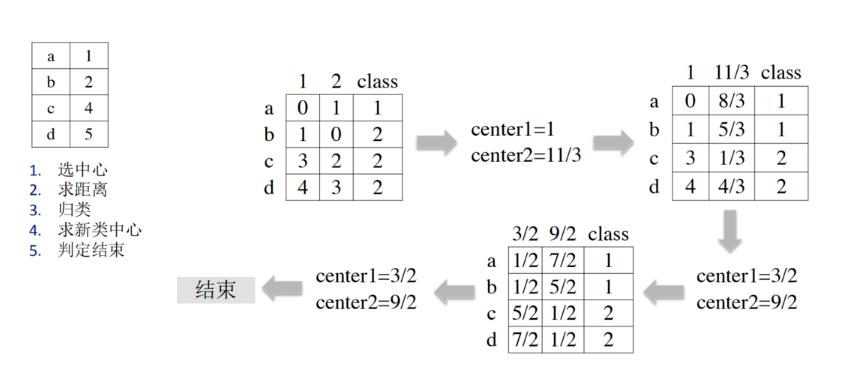
【聚类算法】K-均值聚类(K-Means)算法

4、K-Means演示举例

将a~d四个点聚为两类：
选定样本a和b为初始聚类中心，中心值分别为1、2

【聚类算法】K-均值聚类(K-Means)算法

2.将平面上的100个点进行聚类，要求聚为两类，其横坐标都为0~99。
Python代码演示:

import numpy as np
""" 任务要求：对平面上的 100 个点进行聚类，要求聚类为两类，其横坐标都为 0 到 99。"""x = np.linspace(0, 99, 100)y = np.linspace(0, 99, 100)k = 2n = len(x)dis = np.zeros([n, k+1])
# 1.选择初始聚类中心center1 = np.array([x[0], y[0]])center2 = np.array([x[1], y[1]])iter_ = 100
while iter_ > 0: # 2.求各个点到两个聚类中心距离 for i in range(n): dis[i, 0] = np.sqrt((x[i] - center1[0])**2 + (y[i] - center1[1])**2) dis[i, 1] = np.sqrt((x[i] - center2[0])**2 + (y[i] - center2[1])**2) # 3.归类 dis[i, 2] = np.argmin(dis[i,:2]) # 将值较小的下标值赋值给dis[i, 2]
 # 4.求新的聚类中心 index1 = dis[:, 2] == 0 index2 = dis[:, 2] == 1 center1_new = np.array([x[index1].mean(), y[index1].mean()]) center2_new = np.array([x[index2].mean(), y[index2].mean()])
 # 5.判定聚类中心是否发生变换 if all((center1 == center1_new) & (center2 == center2_new)): # 如果没发生变换则退出循环，表示已得到最终的聚类中心 break
 center1 = center1_new center2 = center2_new
# 6.输出结果以验证print(dis)

结果如下：
其中第 3 项代表聚类：

[[ 34.64823228 105.3589104 0. ] [ 33.23401872 103.94469683 0. ] [ 31.81980515 102.53048327 0. ] [ 30.40559159 101.11626971 0. ] [ 28.99137803 99.70205615 0. ] [ 27.57716447 98.28784258 0. ] [ 26.1629509 96.87362902 0. ] [ 24.74873734 95.45941546 0. ] [ 23.33452378 94.0452019 0. ] [ 21.92031022 92.63098834 0. ] [ 20.50609665 91.21677477 0. ] [ 19.09188309 89.80256121 0. ] [ 17.67766953 88.38834765 0. ] [ 16.26345597 86.97413409 0. ] [ 14.8492424 85.55992052 0. ] [ 13.43502884 84.14570696 0. ] [ 12.02081528 82.7314934 0. ] [ 10.60660172 81.31727984 0. ] [ 9.19238816 79.90306627 0. ] [ 7.77817459 78.48885271 0. ] [ 6.36396103 77.07463915 0. ] [ 4.94974747 75.66042559 0. ] [ 3.53553391 74.24621202 0. ] [ 2.12132034 72.83199846 0. ] [ 0.70710678 71.4177849 0. ] [ 0.70710678 70.00357134 0. ] [ 2.12132034 68.58935778 0. ] [ 3.53553391 67.17514421 0. ] [ 4.94974747 65.76093065 0. ] [ 6.36396103 64.34671709 0. ] [ 7.77817459 62.93250353 0. ] [ 9.19238816 61.51828996 0. ] [ 10.60660172 60.1040764 0. ] [ 12.02081528 58.68986284 0. ] [ 13.43502884 57.27564928 0. ] [ 14.8492424 55.86143571 0. ] [ 16.26345597 54.44722215 0. ] [ 17.67766953 53.03300859 0. ] [ 19.09188309 51.61879503 0. ] [ 20.50609665 50.20458146 0. ] [ 21.92031022 48.7903679 0. ] [ 23.33452378 47.37615434 0. ] [ 24.74873734 45.96194078 0. ] [ 26.1629509 44.54772721 0. ] [ 27.57716447 43.13351365 0. ] [ 28.99137803 41.71930009 0. ] [ 30.40559159 40.30508653 0. ] [ 31.81980515 38.89087297 0. ] [ 33.23401872 37.4766594 0. ] [ 34.64823228 36.06244584 0. ] [ 36.06244584 34.64823228 1. ] [ 37.4766594 33.23401872 1. ] [ 38.89087297 31.81980515 1. ] [ 40.30508653 30.40559159 1. ] [ 41.71930009 28.99137803 1. ] [ 43.13351365 27.57716447 1. ] [ 44.54772721 26.1629509 1. ] [ 45.96194078 24.74873734 1. ] [ 47.37615434 23.33452378 1. ] [ 48.7903679 21.92031022 1. ] [ 50.20458146 20.50609665 1. ] [ 51.61879503 19.09188309 1. ] [ 53.03300859 17.67766953 1. ] [ 54.44722215 16.26345597 1. ] [ 55.86143571 14.8492424 1. ] [ 57.27564928 13.43502884 1. ] [ 58.68986284 12.02081528 1. ] [ 60.1040764 10.60660172 1. ] [ 61.51828996 9.19238816 1. ] [ 62.93250353 7.77817459 1. ] [ 64.34671709 6.36396103 1. ] [ 65.76093065 4.94974747 1. ] [ 67.17514421 3.53553391 1. ] [ 68.58935778 2.12132034 1. ] [ 70.00357134 0.70710678 1. ] [ 71.4177849 0.70710678 1. ] [ 72.83199846 2.12132034 1. ] [ 74.24621202 3.53553391 1. ] [ 75.66042559 4.94974747 1. ] [ 77.07463915 6.36396103 1. ] [ 78.48885271 7.77817459 1. ] [ 79.90306627 9.19238816 1. ] [ 81.31727984 10.60660172 1. ] [ 82.7314934 12.02081528 1. ] [ 84.14570696 13.43502884 1. ] [ 85.55992052 14.8492424 1. ] [ 86.97413409 16.26345597 1. ] [ 88.38834765 17.67766953 1. ] [ 89.80256121 19.09188309 1. ] [ 91.21677477 20.50609665 1. ] [ 92.63098834 21.92031022 1. ] [ 94.0452019 23.33452378 1. ] [ 95.45941546 24.74873734 1. ] [ 96.87362902 26.1629509 1. ] [ 98.28784258 27.57716447 1. ] [ 99.70205615 28.99137803 1. ] [101.11626971 30.40559159 1. ] [102.53048327 31.81980515 1. ] [103.94469683 33.23401872 1. ] [105.3589104 34.64823228 1. ]]
Process finished with exit code 0