《机器人控制系统和MATLAB simulink仿真》笔记1：认识S函数

Posted 2023-04-04 小林up

前言

最近在看控制的东西，想动手实践一下，看到有书名曰《机器人控制系统和MATLAB simulink仿真》，于是学习一下做做产出

1.认识对象：机器人动力学系统的特性

考虑一个关节机器人，其动态性能可由二阶非线性微分方程描述：

$$\mathbf{M}(\mathbf{q})\ddot{\mathbf{q}}+\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})\dot{\mathbf{q}}+\mathbf{G}(\mathbf{q})+\mathbf{F}(\dot{\mathbf{q}})+{\mathbf{\tau }}_{\mathrm{d}}=\mathbf{\tau }$$

其中，$\mathbf{q}\in {\mathbb{R}}^n$为关节角位移量，$\mathbf{M}(\mathbf{q})\in {\mathbb{R}}^{n\times n}$为机器人的惯性矩阵，$\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})\dot{\mathbf{q}}\in {\mathbb{R}}^n$表示离心力和哥氏力，$\mathbf{G}(\mathbf{q})\in {\mathbb{R}}^n$为重力项，$\mathbf{F}(\dot{\mathbf{q}})\in {\mathbb{R}}^n$表示摩擦力矩，$\mathbf{\tau }\in {\mathbb{R}}^n$为控制力矩，${\mathbf{\tau }}_{\mathrm{d}}\in {\mathbb{R}}^n$为外加扰动。

机器人系统的动力学特性为：

（书中没有对这些特性严格地证明，后面还得再琢磨一下）

2.S函数

2.1 S函数简介

S函数是Simulink的重要部分，它为Simulink环境下的仿真提供了强有力的拓展能力。它用文本方式输入公式和方程，适合复杂动态系统的数学描述，并且在仿真过程中可以对仿真参数进行更精确的描述。机器人控制系统的Simulink仿真中，可以使用S函数来实现控制律、自适应律和被控对象的描述。

2.2 S函数使用步骤

一般而言，S函数的使用步骤如下：

(1)创建S函数源文件。创建S函数源文件有多种方法，Simulink提供了很多S函数模板和例子，用户可以根据自己的需要修改相应的模板或例子即可。

(2)在动态系统的Simulink模型框图中添加S-function模块，并进行正确的设置。

(3)在Simulink模型框图中按照定义好的功能连接输入输出端口。为了方便S函数的使用和编写，Simulink的Functions&.Tables模块库还提供了S-functiondemos模块组，该模块组为用户提供了编写S函数的各种例子，以及S函数模板模块。

2.3 S函数的基本功能及重要参数

S函数的基本功能及重要参数设定如下：

(1)S函数功能模块：各种功能模块完成不同的任务，这些功能模块（函数）称为仿真例程或回调函数(call-back functions),包括初始化(initialization)、导数(mdlDerivative)、输出(mdlOutput)等。

(2)NumContStates表示S函数描述的模块中连续状态的个数。

(3)NumDiscStates表示离散状态的个数。

(4)NumOutputs和NumInputs分别表示模块输出和输入的个数。

(5)直接馈通(dirFeedthrough)为输入信号是否在输出端出现的标识，取值为0或1.例如，形如$y=k\times u$的系统需要输入（即直接反馈），其中，$u$是输入，$k$是增益，$y$是输出，形如等式$y=x,x=\dot{u}$的系统不需要输入（即不存在直接反馈），其中，$x$是状态，$u$是输入，$y$为输出。

(6)NumSampleTimes为模块采样周期的个数，S函数支持多采样周期的系统。

除了sys外，还应设置系统的初始状态变量$x_o$、说明变量$str$和采样周期变量$t_s$。t变量为双列矩阵，其中每一行对应一个采样周期。对连续系统和单个采样周期的系统来说，该变量为$[t_1,t_2]$, $t_1$为采样周期，$t_1=-1$表示继承输入信号的采样周期，$t_2$为偏移量，一般取为$0$。对继承输入信号的采样周期的连续系统来说，$t$取为$[一1,0]$。

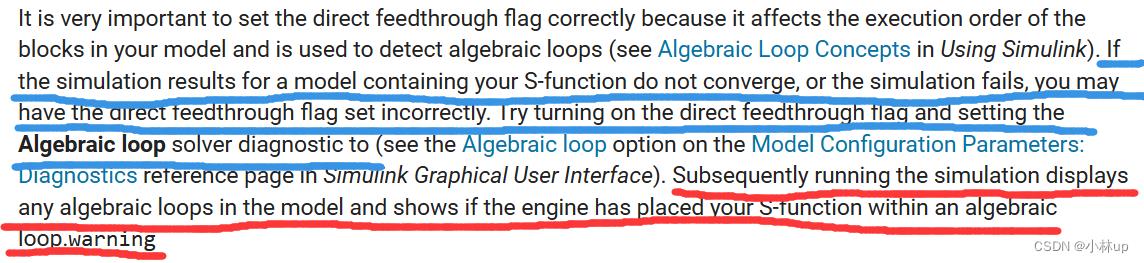
有关采样周期变量的含义更详细的摘录官方文档的内容：
采样周期的取值

如何选择采样时间：

关于以上dirFeedthroug和NumSampleTimes的内容可以参考官方文档理解得更详细：

S-Function Concepts

2.4 S函数的使用实例

以下面的公式为例

$$J\ddot{\theta }=u+d(t)$$

$u$为控制输入,$d(t)$为加在控制输人端的扰动,模型输出为角度$\theta$和角速度$\dot{\theta }$，$J$是转动惯量，模型描述为：

$$\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=\frac{1}{J}(u+d(t))\end{array}$$

其中$x_1=\theta ,x_2=\dot{\theta }$是状态变量。

2.4.1 模型初始化Initialization函数

上述动力学方程是1输入2输出系统，角度$\theta$和角速度$\dot{\theta }$的初始值为0，模型初始化参数为[0,0]，模型初始化S函数为：

function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates  = 2;%连续状态个数为2：x_1和x_2，因为采用连续采样周期仿真
sizes.NumDiscStates  = 0;%离散状态个数为0
sizes.NumOutputs     = 2;%输出量为2个：角度和角速度
sizes.NumInputs      = 1;%输入量为1个，u
sizes.DirFeedthrough = 0;%方程中输入没有直馈于输出
sizes.NumSampleTimes = 1;%采样周期数是1
sys simsizes(sizes);
x0=[0,0]:%初始化输出值角度和角速度都是0
str=[]:%无其他说明
ts=[0 0]:%连续采样，第一个值为0，没有偏移，第二个值也设为0

2.4.2 微分方程描述的mdlDerivative函数

该函数可用于描述微分方程并实现数值求解。在控制系统中，可采用该函数来描述，被控对象和自适应律等，并通过Simulink环境下选择数值分析方法(如ODE方法)实现模型的数值求解。取$J=2$,$d(t)=\sin t$,则采用S函数可实现该模型角度$\theta$和角速度$\dot{\theta }$的求解，描述如下：

function sys=mdlDerivatives(t,x,u)%sys
J=2;
dt=sin(t);
ut=u(1);
sys(1)=x(2):%左边的sys是状态变量的导数
sys(2)=1/J (ut+dt);

2.4.3 用于输出的mdlOutput函数

S函数的mdlOutput函数通常用于描述控制器或模型的输出。采用S函数的mdlOutput模块来描述模型角度$\theta$和角速度$\dot{\theta }$的输出：

function sys mdlOutputs(t,x,u)
sys(1)=x(1):
sys(2)=x(2):

Matlab Simulink系统仿真（01）

Matlab简介

Matlab基本界面介绍

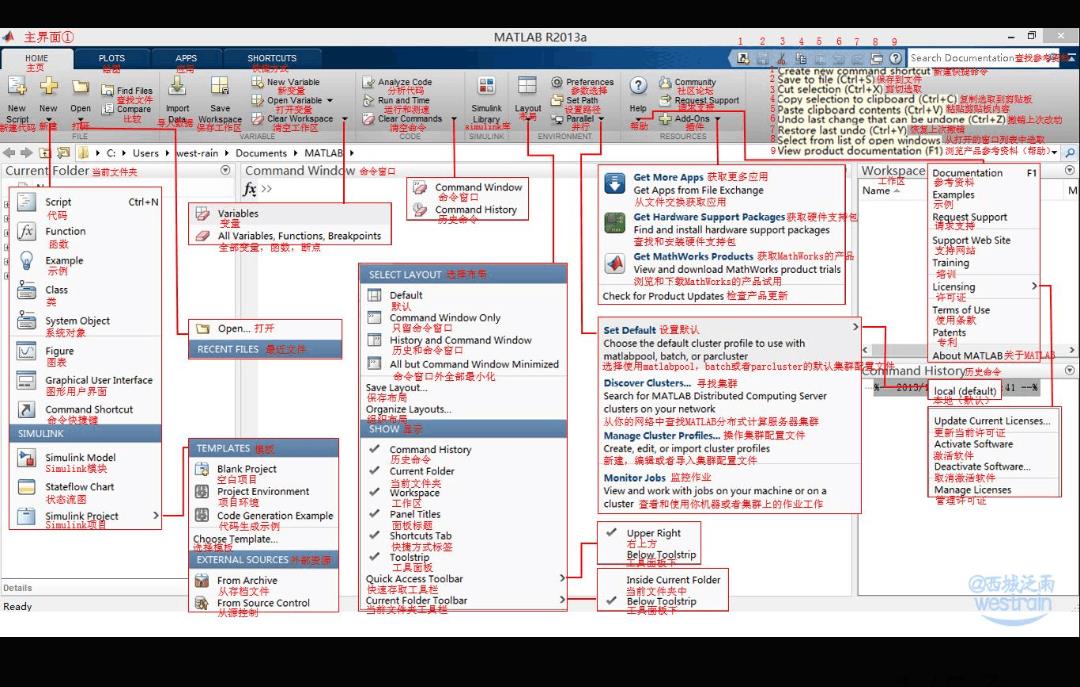
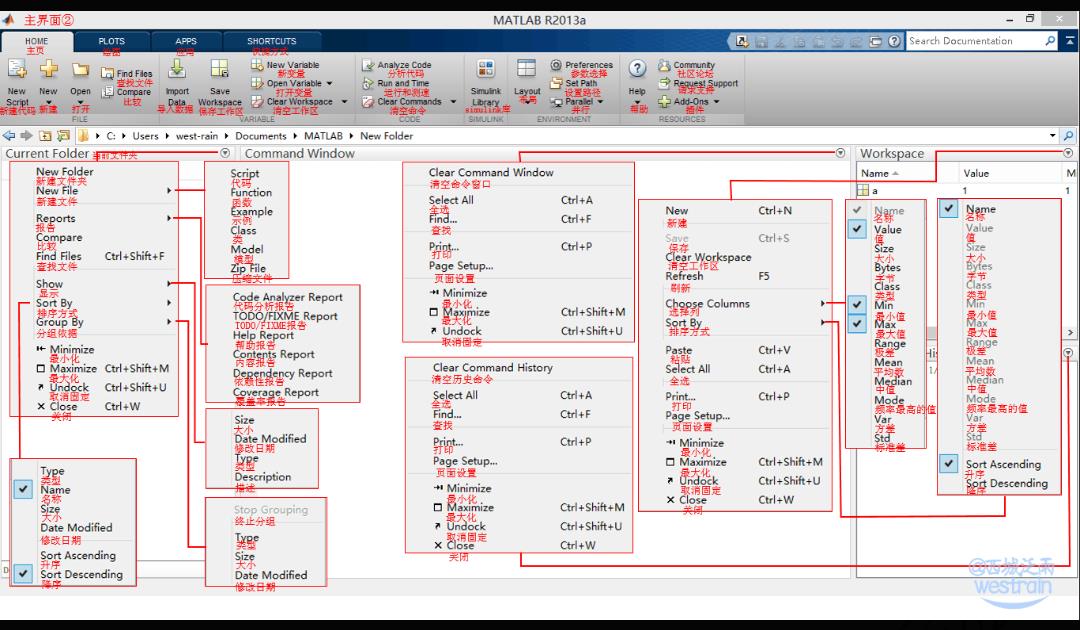
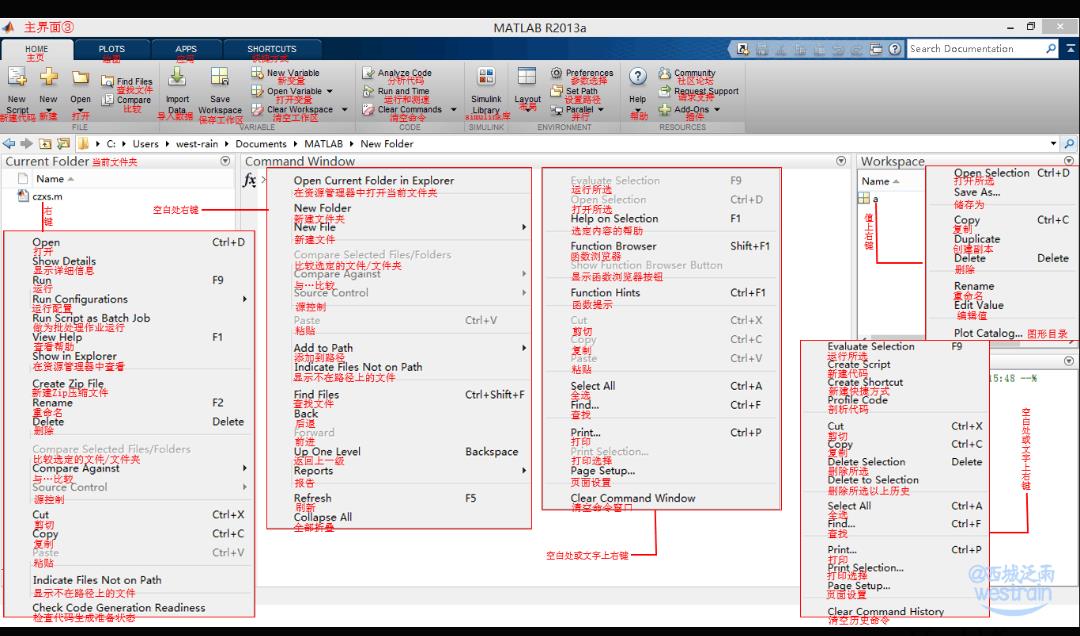
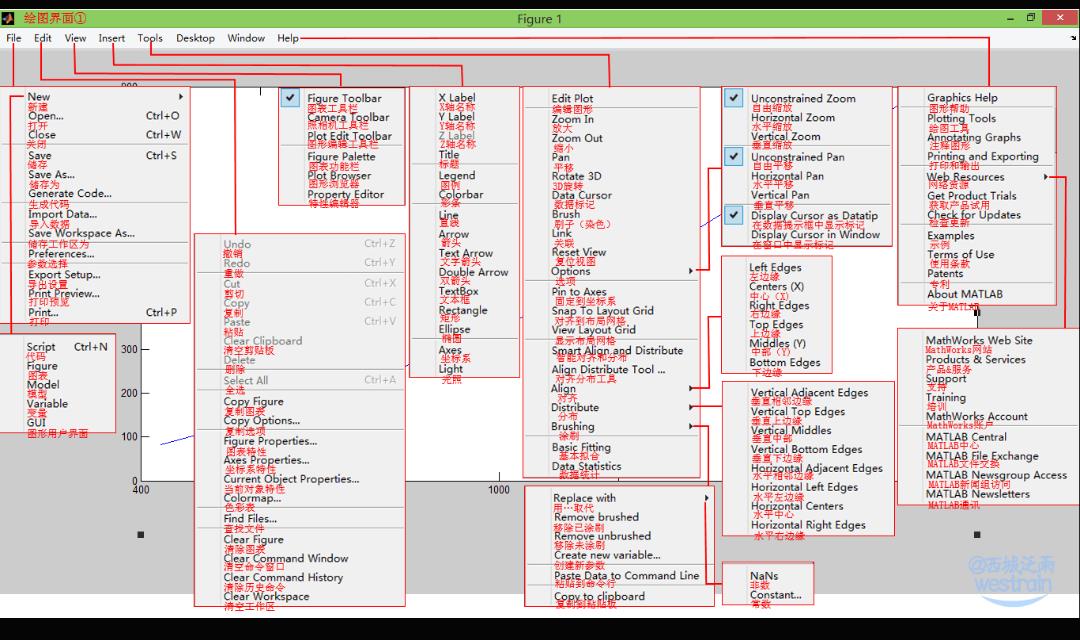
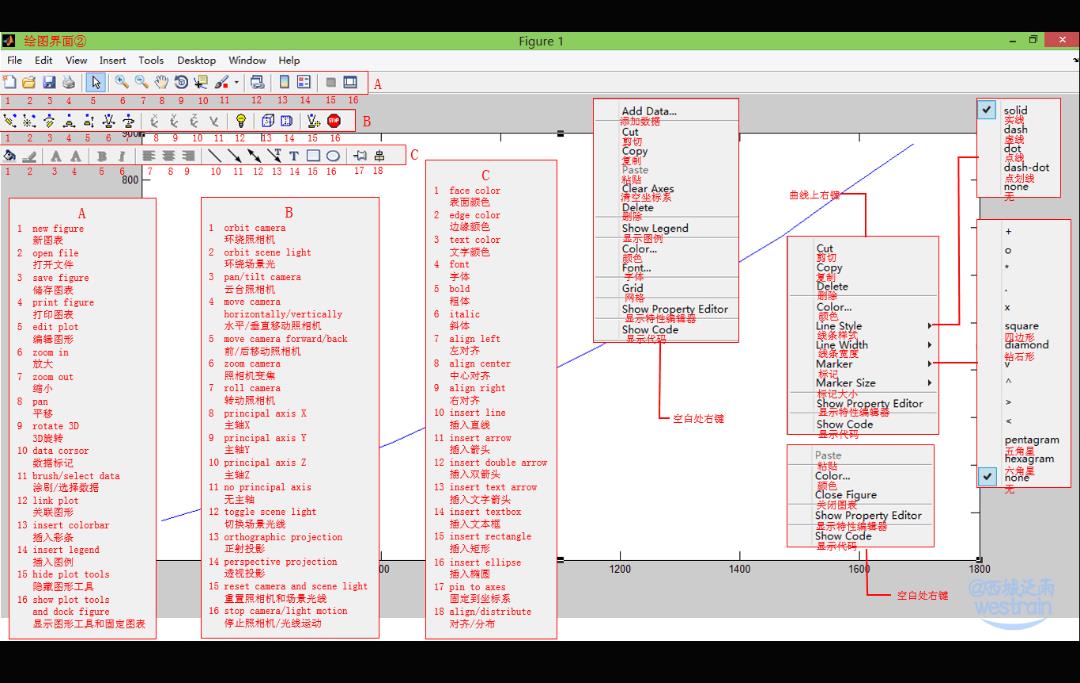
Matlab的主要特点

1.具有丰富的数学功能
2.具有很好的图视系统
3.可以直接处理声音和图形文件
4.具有若干功能强大的应用工具箱
5.使用方便，具有很好的扩展功能
6.具有很好的帮助功能

M文件
脚本M文件
函数M文件

Matlab中的预定义变量

变量	含义
Ans	分配最新计算表达式的值
Eps	返回机器精度
Realmax	返回机器技能处理的最大浮点数
Realmin	返回机器技能处理的最小的非零浮点数
Pi	π，3.14159265
Inf	定义为1/0
NaN	Not a Number
who	列出已定义的变量
who global	与who相同，仅列出全局变量
who a*	给出所有以a开头的变量的一个列表
whos	给出比who更加详细的列表
whos global	与whos相同，仅列出全局变量
clear	删除所有变量
clear global	删除全局变量
clear all	删除所有变量
clear var1	删除变量var1
clc	清除屏幕
exit,quit	退出
ctrl+c	中断

Matlab数据类型

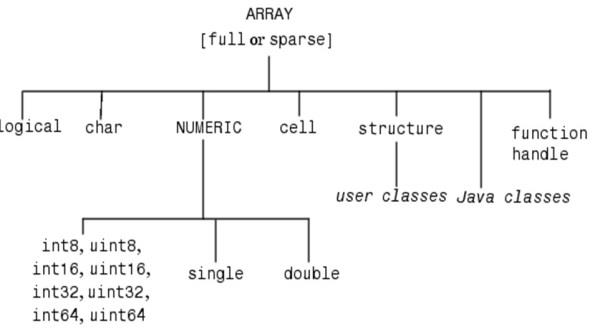
Matlab元胞数组（cell数组）：
cell数组可以把不同类型的数据纳入到一个数组变量中







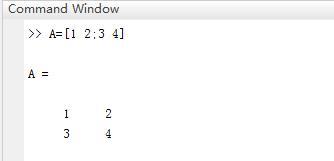
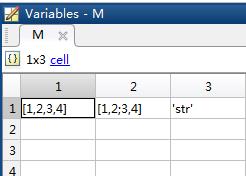
Matlab结构数组：

s = struct('filed1',value1,'filed2',value2,...)

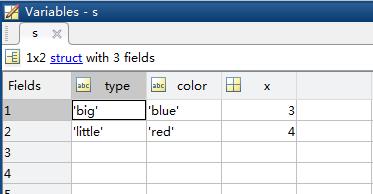
将每个字段的数组的一行一列重新赋值



Matlab的基本计算
矩阵计算
+加法 -减法 *乘法 ^幂次 \\左除 /右除 ‘转置 inv求逆 eig特征值 poly特征多项式
数组计算
.+加法 .-减法 .*乘法 .^幂次 .\\左除 ./右除 .‘共轭

Matlab的符号计算
例如：

y = sym(‘2*sin(x)*cos(x)’)
w = sym('[1/(a+x),sin(x),(b-a)/(a+x);1,exp(x),x^2]')

symadd(A,B)		//两个符号矩阵的和
symsub(A,B)		//两个符号矩阵的差
symmul(A,B)		//两个符号矩阵的积
symdiv(A,B)		//两个符号矩阵的除
inverse(A)	//符号矩阵求逆

符号微积分
微分：diff(f)
积分：int(f)
符号代数方程式求解
线性方程组;
X=linsolve(A,B) //特解
[X,Z]=linsolve(A,B) //通解
一般代数方程的解
solve(S)
符号微分求解
[y1,y2]=dsolve(a1,a2)

二维曲线图形

plot(y)
plot(x,y)
subplot(M,N,P)

例如:
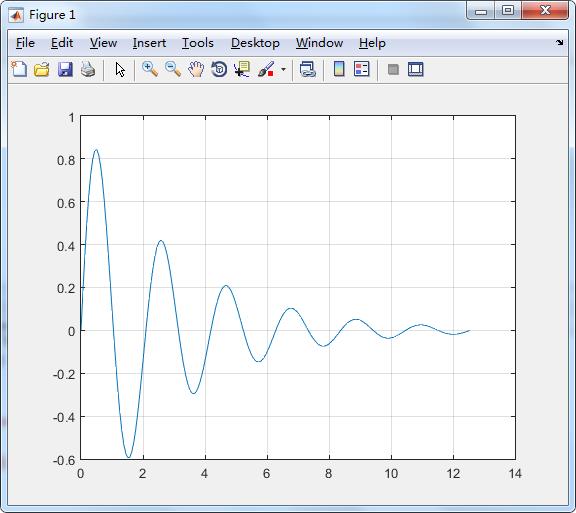
画出衰减震荡曲线y=e^(-t/3) sin3t

t=0:pi/50:4*pi;
y=exp(-t/3).*sin(3*t);
plot(t,y)
grid

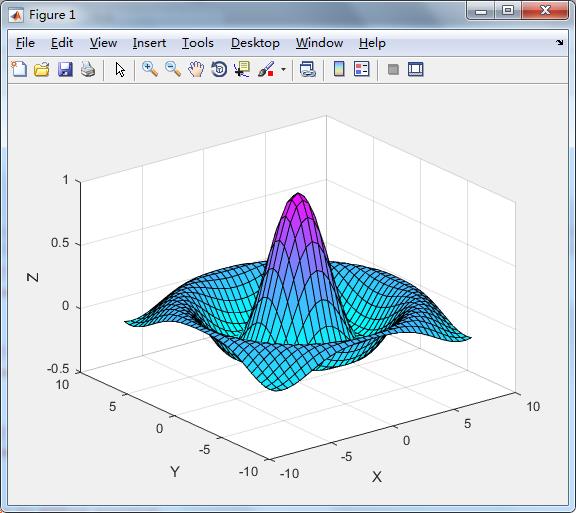
clear;
x=-8:0.5:8;
y=x';
X=ones(size(y))*x;
Y=y*ones(size(x));
R=sqrt(X.^2+Y.^2)+eps;
Z=sin(R)./R;
surf(X,Y,Z);
colormap(cool)
xlabel('X'),ylabel('Y'),zlabel('Z')