Transformer的基本原理

Posted zhiyong_will

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Transformer的基本原理相关的知识，希望对你有一定的参考价值。

1. Seq2Seq框架

1.1. Seq2Seq框架概述

Seq2Seq[1]框架最初是在神经机器翻译（Neural Machine Translation，NMT）领域中提出，用于将一种语言（sequence）翻译成另一种语言（sequence）。其结构如下图所示：

在Seq2Seq框架中包含了Encoder和Decoder两个部分。在Encoder阶段，通过神经网络将原始的输入 x 1 , x 2 , ⋯   , x T x \\left \\ x_1,x_2,\\cdots,x_T_x\\right \\ x1​,x2​,⋯,xTx​​转换成固定长度的中间向量 c 1 , c 2 , ⋯   , c l \\left \\ c_1,c_2,\\cdots,c_l \\right \\ c1​,c2​,⋯,cl​，在Decoder阶段，将此中间向量作为输入，得到最终的输出 y 1 , y 2 , ⋯   , y T y \\left \\ y_1,y_2,\\cdots,y_T_y \\right \\ y1​,y2​,⋯,yTy​​。

1.2. 建模方法

在Encoder和Decoder部分，需要模型能够对时序数据建模，在NLP中，通常使用两种方式对时序数据建模，一种是以RNN[2]，LSTM[3]为主的建模方法；另一种是以CNN[4]，[5]为主的建模方法。

以RNN为例，其基本机构如下图所示：

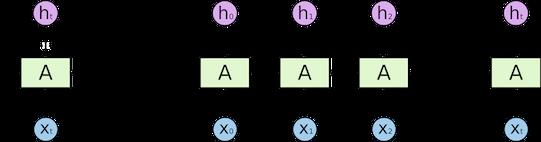
在基于RNN的建模方法中， t t t时刻的状态更新依赖于 t − 1 t-1 t−1时刻的输出，即 t t t时刻的状态更新公式为：

h t = f ( U h t − 1 + W x t + b ) h_t=f\\left ( Uh_t-1+Wx_t+b \\right ) ht​=f(Uht−1​+Wxt​+b)

在RNN的基础上衍生出很多优化的方案，如对于长距离依赖问题的优化，提出了LSTM以及GRU等模型；对于单向建模能力的问题，提出了双向的RNN模型，提升了对时序数据的建模能力。以简单的RNN为例，从上可以看出，RNN最大的问题是不容易并行化。因为 t t t时刻的状态更新依赖于 t − 1 t-1 t−1时刻的输出，所以必须先计算出 t − 1 t-1 t−1时刻的输出。

第二种是CNN的建模方法，以TextCNN[4]，[5]模型为例：

以最外层的红色为例，设置不同的filter的大小 N N N，如上图中filter的大小为2，通过filter的移动，可以计算filter内 N N N个词之间的相互依赖关系。与RNN相比，基于CNN的建模方法中，filter的计算是完全可以并行计算，是对RNN计算效率的极大提高。CNN与RNN对词的建模可以通过下图[6]进一步说明。

从图中可以看出，CNN和RNN都是对变长序列的一种“局部编码”：卷积神经网络是基于N-gram的局部编码；而对于循环神经网络，由于梯度消失等问题也只能建立短距离依赖。要解决这种短距离依赖的“局部编码”问题，建立输入序列之间的长距离依赖关系，可以使用以下两种方法：一种方法是增加网络的层数，通过一个深层网络来获取远距离的信息交互，另一种方法是使用全连接网络[6]。全连接网络如下图所示：

然而，全连接网络虽然可以对远距离依赖建模，但是无法处理变长的输入序列，同时，在全连接网络中，缺失了词之间的顺序信息。不同的输入长度，其连接权重的大小也是不同的。

综上，基于RNN，CNN以及全连接网络建模方法存在着以下的问题：

  • 长距离依赖问题（RNN，CNN）
  • 并行问题（RNN）
  • 变长输入问题，词序信息问题（全连接网络）

1.3. Self-Attention

为了能提升Seq2Seq框架的性能，在Seq2Seq框架中引入了Attention机制[7]，Attention机制通过对训练数据的学习，对其输入 x \\mathbfx x的每一个特征赋予不同的权重，从而学习到对于目标更重要的信息，让模型具有更高的准确率。在Seq2Seq中引入Attention机制如下图所示：

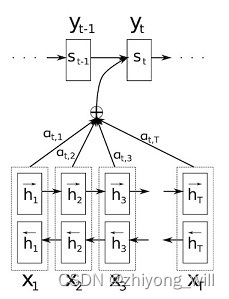
其中，Attention的计算体现在针对不同的Decoder输出 y t y_t yt​，都有一个对应的上下文向量 c t c_t ct​， y t y_t yt​的计算公式为：

y t = f ( y t − 1 , s t − 1 , c t ) y_t=f\\left ( y_t-1,s_t-1,c_t \\right ) yt​=f(yt−1​,st−1​,ct​)

其中， c t c_t ct​为：

c i = ∑ j = 1 T x α i j h j c_i=\\sum_j=1^T_x\\alpha _ijh_j ci​=j=1∑Tx​​αij​hj​

其中， α i j \\alpha _ij αij​为归一化权重，其具体为：

α i j = e x p ( e i j ) ∑ k = 1 T x e x p ( e i k ) \\alpha _ij=\\fracexp\\left ( e_ij \\right )\\sum_k=1^T_xexp\\left ( e_ik \\right ) αij​=∑k=1Tx​​exp(eik​)exp(eij​)​

其中， e i j e_ij eij​表示的是第 i i i个输出前一个隐藏层状态 s i − 1 s_i-1 si−1​与第 j j j个输入隐层向量 h j h_j hj​之间的相关性，可以通过一个MLP神经网络进行计算，即：

e i j = a ( s i − 1 , h j ) = v a T t a n h ( W a s i − 1 + U a h j ) e_ij=a\\left ( s_i-1,h_j \\right )=v_a^Ttanh\\left ( W_as_i-1+U_ah_j \\right ) eij​=a(si−1​,hj​)=vaT​tanh(Wa​si−1​+Ua​hj​)

上述的公式也表示了一般性的Attention的计算过程，即：