回归分析常数项t值没有显著异于零怎么办_一文详解经典回归分析

Posted 2022-08-26 weixin_39890543

在如今机器学习、数据科学、人工智能热潮下，回归分析似乎成了家喻户晓的东西。实际上回归分析自Galton爵士提出以及Pearson和Fisher的理论的加持，经过一百多年的发展，早已成了发现客观规律的有力武器。回归分析的文章已经多得数不胜数了，这篇文章也许会有点不同：我一直力求详细。这篇文章是一文详解t检验的延续，从一元线性回归的理论出发，涉及到回归系数的估计、无偏性的证明、方差的计算、显著性检验和预测，再推广到多元线性回归模型（用矩阵来研究会非常方便）。

从函数到回归模型

早在初中我们就学过一元一次函数：

给定

后，这是一条 确定的直线， 只需要两点就可以确定的直线，给出一个新的 ，就可以唯一确定一个落在这条直线上的 。这为我们线性回归的思想打下了基础。我们在等号右边加一个随机扰动项（又叫噪声，noise），就成了一元线性回归模型：

只不过我们更习惯这样的表达：

代表每一个样本点，取的是个体的英文identity的首字母。

要注意的是(1)式不是回归模型，(2)式才是。究其原因在于(1)式代表一条确定的直线，而(2)式含有未知的随机扰动项。只有含随机扰动项的才是回归模型。回归模型与直线的相同点是自变量和因变量都是线性关系，不同点在于前者是不确定的，后者是确定的。

世界纷繁复杂，确定相比不确定简直是小巫见大巫。(2)式是真实的客观规律，但是未知、不可观测的。但我们可以假设要研究的因变量

关于自变量 的条件期望是自变量 的确定的线性关系，即：

假设中的

是未知的，称之为 回归系数。为了检验这个假设，我们要利用样本数据估计出 ，将它们的估计值记为 ，由此得出的相应的 的估计值为 ，这样(3)式变为：

(4)式称为经验回归方程，这是对真实的、不可观测的(2)式的估计。

是 被解释变量(dependent variable)、 响应变量(response)、内生变量， 是 解释变量(independent variable)、外生变量。 但一般 是人为给定的常量，只有 是变量。

(2)、(3)和(4)可以推广到多个解释变量的情形：

基本假定

基本假定是对于随机扰动项

来说的，它有两个基本假定：

1. 零均值、等方差、无自相关（Gauss-Markov假定）

1. 正态分布、相互独立假定

相互独立

其中

未知。 这两个基本假定是不一样的。

由于

都是常数，那么 也是正态变量：

这一点在后面的推导中很有用。

一元线性回归模型

这部分我们结合向量来推导。对于

个样本，即 ，我们可以将被解释变量、解释变量、回归系数和随机扰动项表示为向量：

其中随机扰动项

满足基本假定，有：

其中

为 阶单位方阵。在解释变量前面添加全1向量形成 设计矩阵(Design Matrix)：

这样模型可改写为：

1.利用最小二乘法估计回归系数并证明存在且唯一

估计回归系数的一种方法是最小二乘法(Least Square Method, LSE)，为了与广义最小二乘法相区别，有人也称之为普通最小二乘(Ordinary Least Square, OLS)。如果回归方程对样本拟合得较好，能较好地反映客观规律，那么真实值

和回归值 的“距离”会较小。对于这个“距离”的定义，我们采用残差平方和：

其中

是残差平方和Sum of Squares for Error的缩写。令 取得最小值的 ，就是它们的最小二乘估计（记得要加一个帽子）：

只需要对于

求偏导数并令其为0：

这两式进一步化简：

解方程组（加帽子）：

得到最小二乘估计：

实际上

的表达式可以接着化简（若不加说明， 表示 ）：

不妨记：

那么(13)可以写为：

实际上(13)还可以改写为：

或者：

(14)在后面会用到。

有一个问题，这里求偏导数并令其为0得到的是

的极小值点，如何证明它就是函数的最小值点？我们需要考察 关于 的 矩阵：

由于

是对称阵，若它满秩，则它正定，那么 的极小值点就是最小值点，且唯一。而它满秩的充要条件是向量 与全1向量不线性相关。这个条件一般情况下都满足的。

我们定义残差

，从而残差向量：

那么(9)和(10)说明了如下事实：

也就是说

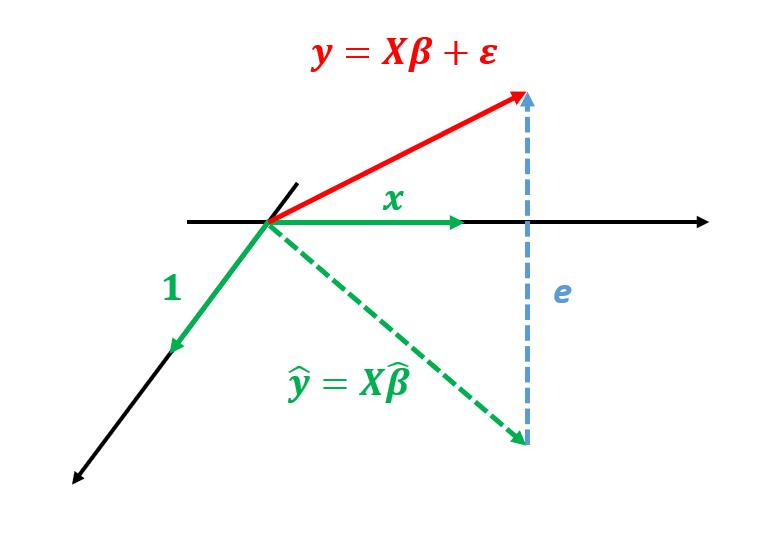
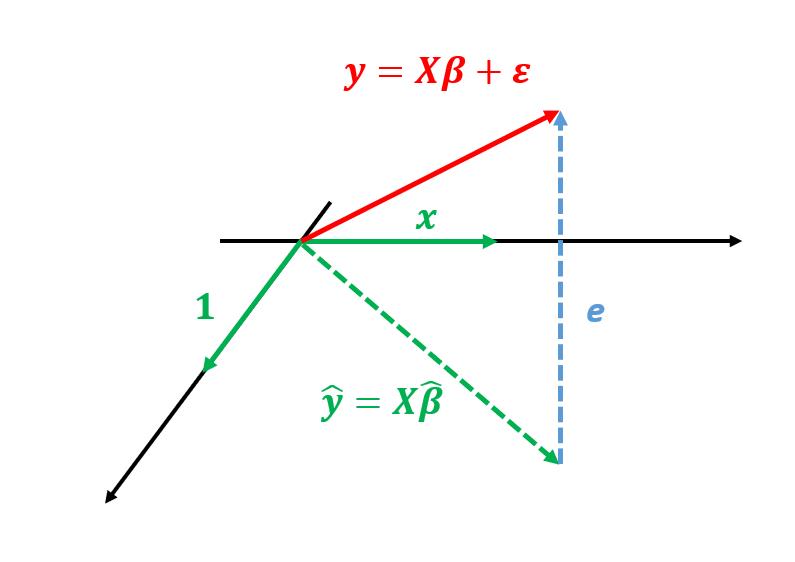
向量、 向量都与残差向量 正交。实际上设计矩阵 是由 向量、 向量组成的，它可以看成由这两个向量张成的平面，估计值 是 向量、 向量的线性组合，落在 平面上。真实值 是空间中的一条向量，残差向量 与 平面正交（如图所示）。这也说明了估计值 与真实值 的关系：估计值 是真实值 向 平面的投影。

2.极大似然估计

上面使用了最小二乘法来估计回归系数，也可以考虑极大似然估计(Maximum Likelihood Estimation, MLE)。由于

是正态变量，有密度函数：

样本的似然函数：

其中

是之前定义过的残差平方和：

。

对数似然函数：

其中

是与 无关的常数。

令对数似然函数取得最大值的必要条件：

解得：

再将上式带回对数似然函数：

它取得最大值

取得最小值，说明极大似然估计与最小二乘法是等价的。实际上也可以对对数似然函数分别关于 求偏导并令其为0，最终化简得到的表达式与最小二乘法对残差平方和进行的操作得到的结果是一样的。

3.一些性质

先证明

关于 的 线性性质。由(14)：

其中

。说明了 关于 的线性性质。令：

则：

考察

，由(11)、(17)：

说明了

关于 的线性性质。下面考察 无偏性。

由(11)：

接着考虑回归系数的方差及它们的协方差。

首先给出引理：

Lemma 1

若 ， ，则：
若 ，则：

根据Lemma 1：

由Lemma 1、(18)和(19)：

上式还可以接着化简：

由(11)、(17)、Lemma 1和(19)，考察它们的协方差：

给定解释变量一个新的取值

，考虑 的方差。由(19)、(20)和(22)：

实际上

不一定要是新值，也可以是某个已有的样本 ，那么它相应的被解释变量的预测值 的方差：

一定要与真实值

的方差区分：

4.假设检验

回到开始的问题，我们要验证建立这个模型的假设是否成立，也就是进行假设检验。有两个假设检验需要做，一个是对回归系数的显著性

检验，一个是对方程总体的显著性 检验。

要检验解释变量

对被解释变量 的影响是否显著，也就是做如下假设检验：

当

时， 与 无关，那么 对 的影响不显著。但 是未知的，我们只能根据它的估计值 来作检验。根据 是关于 的线性函数，且 是正态变量，那么 也是正态变量：

当

成立时：

我们首先回顾一下

统计量的构造定义：

若

且 相互独立，那么：

然而要构造一个

统计量有一个非常漫长的过程但这是值得的，在这个过程中我们还能定义一些概念，方便 检验使用。根据 统计量的构造定义，我们需要找到 相互独立的标准正态变量和卡方变量。

我们首先就定义

和 ：

总离差平方和：
回归平方和：
残差平方和：

实际上

。下面证明 总离差平方和分解式 ，最后两个等号应用了(8)、(16)：

考虑上式中的最后两项，由(8)和(15)、(16)的向量化表达：

从而：

。实际上平方和分解式也可以不用向量化运算，用三个平方和定义中的第一个等号的式子展开后，也就是证明：

根据(4)、(15)、(16)，上式左边等于：

由：

两式相减得到：

我们先给出

的另一种表达，并利用它给出 的期望，根据(23)：

考虑它的期望，要用到(19)：

我们再考虑

，其中用到(2)和(4)：

计算它的期望，其中用到(15)、(16)、(19)、(20)和(22)：

下面考虑

，要用到(15)、(16)、(18)以及 和 的独立性( )：

再考虑

：

由(25)、(26)得到：

将(28)、(29)带入(25)得到：

(30)式实际上说明了

是 的无偏估计，记作 。由于 未知，我们需要利用样本信息来估计它，现在已经找到了它的无偏估计。 这一点在构造 统计量中非常关键。在之后我会给出它的另一个证明（见(42)）。

接着就是寻找一个卡方变量，这一部分在一文详解t检验中的4.回归系数的显著性检验和附录2.3已经给出，只需取

即可。那么我们得到了与标准正态变量独立的卡方变量（独立性的证明见一文详解t检验 附录2.4）：

其中

。现在我们需要找到一个标准正态变量，实际上我们之前就得到了：

我们只需对它标准化：

那么

：

实际上：

是

的标准差的无偏估计：

回到假设检验：

给定显著性水平

，查自由度为 的 分布表得到分位数 ，若根据样本计算得到的 ，则拒绝原假设，即 对 的影响是显著的，否则认为不显著。假设检验和置信区间等价，那么 的 置信区间为：

实际上也可以对

做假设检验（意义不大）：

类比

的 统计量的构造，根据(21)，对于 ：

假设检验和置信区间的步骤也是类似的。

关于线性回归方程整体的显著性

检验可以参考一文详解F检验中的 3.线性回归方程整体的显著性检验。只需取 即可：

统计量及方差分析表：

当

时拒绝原假设，认为回归方程整体是显著的，否则不显著。

对于一元线性回归，

检验和 检验是等价的，因为根据(24)和(33)：

这说明

统计量的值是 统计量的平方，根据数理统计可以知道自由度为 的 变量的平方就是自由度为 的 变量。它们的分位数也相同，故检验是等价的。

实际上对于一元线性回归，还有一种检验：相关系数检验可以做。相关系数的定义：

对这个定义稍加推导：

得到

与 的关系，且它们符号相同。这一点很容易理解， 是相关系数， 是经验回归方程的斜率，它们符号肯定是相同的。再给出相关系数检验统计量前，首先给出一个结论：**对于一元线性回归，这三个检验是等价的。 为了说明这一点，我们首先给出决定系数(Coefficient of Determination)**的概念：

根据第一个等号，直观上它的意义就是

占 的比例，也就是回归平方和占总离差平方和的比例，也就是 回归方程能解释的被解释变量的变差占被解释变量总变差的比例。显然这个值越接近1说明拟合效果越好， 但未必拟合效果越好的就越实用，也许模型是有结构性问题的。

实际上又有一个结论：对于一元线性回归，可决系数等于相关系数的平方（神奇的一元线性回归！），利用(24)容易得到证明：

利用(34)、(35)和(36)我们就可证明

检验和 检验的等价性，并给出 检验统计量：

(37)说明了

检验和 检验的等价性，最后一个等号就是 检验统计量，假设检验的步骤与 检验相同。根据(34)、(37)就说明了 的等价性。实际上由(34)、(36)和(37)可以很容易地导出 与 （或 ） 的关系，这里就不给过程了：

或

需要强调的是，(34)到上式的这些结论只对一元线性回归成立。

接下来我们研究残差

的性质，并利用由此导出的一些结论研究响应变量新值的预测问题。回顾一下残差的定义：

由(15)和(16)很自然地可以得到：

由此可以导出残差向量与1向量和x向量正交，这也是之前就提到过的。下面计算残差的平方：

其中

是之前已经得到的结论。问题转化为求最后一项。先给出第一种方法，利用残差与1向量和x向量的正交性：

上述步骤中有

，说明 残差和预测值不相关。残差的方差：

另一种方法考虑向量化运算，先定义除第

个位置为1外，其余位置全为0的向量：

那么：

根据Lemma 1：

与之前的结果一致。我们可以定义这个结果为：

称作杠杆值。它可以用来度量第

个样本点对于回归方程的影响程度。因为当 离 的距离很远，那么杠杆值取值较大，对于回归方程的影响较大。高杠杆值的点称为 高杠杆点(high leverage case)，是离群点、异常点。

结合杠杆值的定义，残差的平方可以写为：

之前说过要给出(30)的另一种证明。回顾这个定义：

那么：

预测值的方差可以写为：

说明高杠杆点的响应变量的预测值的方差较大。说明高杠杆点不仅影响回归方程也影响自身预测值的波动程度。下面就来考察一下给定解释变量新值

，响应变量新值 的点估计（也可叫预测）、区间估计和 响应变量新值的期望的区间估计。之前遗漏了一个简单但很重要的结论：

也即

。该式给出了响应变量新值 的点估计就是 。 但要注意的是， 是随机变量，不能说 是 的无偏估计，只能说 是 的无偏估计，或者说 是 关于 的条件期望的无偏估计。

实际上还有：

之前也得到了：

实际上

是 的线性组合，而它们又是之前观测的 个样本 的线性组合，而新值 与之前 个观测是独立的，那 与 独立（这一点很重要），那么：

但

未知，只能用它的无偏估计 替换，与 的预测区间类似，正态变量变为 变量，从而 的 预测区间为：

由于新值

的期望 是一个常数，故：

从而新值的期望的

的预测区间为：

从(49)和(50)可知新值的预测区间和新值的期望的预测区间只相差根号下的1。

多元线性回归模型

模型形式：

写为矩阵形式：

其中：

除了两个基本假定：

1. 零均值、等方差、无自相关（Gauss-Markov假定）

1. 正态分布、相互独立假定

相互独立

多元的情形还需增加一条：

1. 是满秩矩阵，即 。且要求样本量大于解释变量的个数： 。

有关回归系数的估计值、系数显著性和方程显著性的假设检验详见一文详解t检验和一文详解F检验。这里给出：

令

。则 统计量和 统计量：

其中

是 的无偏估计， 的定义同前：

总离差平方和： 回归平方和： 残差平方和：

令：

表示解释变量的新值。类似一元的情形，响应变量新值的区间预测和响应变量新值的期望的区间预测：

接着要介绍广义

检验。实际上上述 检验是广义 检验的特殊情形。我们记s：

为了加以区分，我们将

的 的预测值、 的估计值和三种平方和都加一个角标0： 。对于 我们施以最小二乘法：

可以发现它的残差平方和：

是等于

的总离差平方和的。又由于 ，那么 的 统计量可以写为：

分母仍然是原始

统计量的分母。分子是残差平方和之差，并除以两模型解释变量个数的差 （这就是残差平方和之差的自由度），这里 。根据这个思想，我们可以将 作为基准模型。基准模型可以按照我们的假设变化，而 不变，这样就能将 检验推广至一般的情形。举一个例子就容易理解：

相较 少了解释变量 。对这两个模型进行对比的 检验就是：

等价于：

其中：

那么：

分别计算这两个残差平方和，带入计算、查表即可做检验。实际上，“

表示两模型解释变量个数的差”这一说法不严谨，应该说 。下面正式给出广义 检验：

广义

检验

这部分详细内容见线性回归模型中的一般的F检验

一般地，对于矩阵

，且 ，做假设检验：

其

统计量：

该检验的意义与

有关。当 ，该检验就是一般的 检验。

再举一个例子加深印象。对于回归模型：

作检验：

这等价于：

其中：

且

。在 成立的条件下：

实际上可以令

，作回归：

再计算两个模型的残差平方和

，代入公式计算统计量、查表、得出结论。

实际上广义

检验可以与 检验等价。也就是作检验：

等价于：

其中

表示除第 个元素为1，其余元素全为0的行向量。 。将 剔除解释变量 得到 。计算残差平方和，带入公式：

说明了两种检验的等价性。

也称为偏 统计量。

拟合优度

多元线性回归也有决定系数的概念：

但它不等于

与某个解释变量的相关系数的平方。容易证明：

的自由度为 ， 的自由度为 ，当解释变量的个数 增加而样本量 不变时， 势必会减小，导致 增大。这就可能导致对于同一个相应变量做两个回归模型，其中一个解释变量个数比另一个多，导致其拟合优度较高，然而事实上该模型其他检验结果并不如另一个模型。这就引入了 修正的决定系数(Adjusted Coefficient of Determination)：

实际上就是对两个平方和分别除以它的自由度。容易证明：

这个概念给了两个解释变量个数不同的模型的比较以依据。修正的决定系数越大，拟合优度越好。