请教一个关于二维数组的算法

Posted 2023-04-04

在下面这样一个6×9二维数组中，需要找出满足1,1,4,1,1这样排列的组合来，记录它们的坐标。

int Array[6][9] =

1,1,0,1,0,0,1,0,0,
4,1,1,0,0,0,1,4,0,
4,0,0,1,1,4,4,1,0,
0,0,0,0,0,1,0,1,0,
0,0,1,1,4,1,0,1,0,
0,0,0,0,4,0,0,0,0,
;

算法越简单越好，能有具体代码更好，我会追加积分的，多谢各位～～
谢谢各位，忘记说清楚了，需要这5个数相连，顺序满足1，1，4，1，1，只能横竖相连，不能斜线相连，

如果仅仅对于6×9这么小的矩阵来说，可以直接循环寻找各个方向的匹配，源代码如下:

#include <cstdio>
#include <cstring>
using namespace std;

int Array[6][9] =

1,1,0,1,0,0,1,0,0,
4,1,1,0,0,0,1,4,0,
4,0,0,1,1,4,4,1,0,
0,0,0,0,0,1,0,1,0,
0,0,1,1,4,1,0,1,0,
0,0,0,0,4,0,0,0,0,
;

int mo[5] = 1,1,4,1,1;

bool check_right(int a,int b) //右方向

int i;
for (i=0;i<5;i++) if (b + i >= 9) return false;
else if (Array[a][b + i] != mo[i]) return false;
return true;


bool check_down(int a,int b) //下方向

int i;
for (i=0;i<5;i++) if (a + i >= 6) return false;
else if (Array[a + i][b] != mo[i]) return false;
return true;


bool check_left_down(int a,int b) //左下方向

int i;
for (i=0;i<5;i++) if (a + i >= 6 || b - i < 0) return false;
else if (Array[a + i][b - i] != mo[i]) return false;
return true;


bool check_right_down(int a,int b) //右下方向

int i;
for (i=0;i<5;i++) if (a + i >= 6 || b + i >= 9) return false;
else if (Array[a + i][b + i] != mo[i]) return false;
return true;


int main()

int i,j;
for (i=0;i<6;i++)
for (j=0;j<9;j++)

if (check_right(i,j)) printf("%d %d right\n",i,j);
if (check_down(i,j)) printf("%d %d down\n",i,j);
if (check_left_down(i,j)) printf("%d %d left_down\n",i,j);
if (check_right_down(i,j)) printf("%d %d right_down\n",i,j);
// 由于模板文本具有回文性质,故只需匹配4个方向,若对于任意模板文本,追加检查剩余的四个方向即可.

return 0;


若对于较为巨大的矩阵以及较多的模板文本，（例如500×500的矩阵，500个文本），如果需要在较短的时间内完成算法（如1秒）需要使用后缀自动机，具体到这个问题就是trie图，一种基于后缀有限状态自动机（Suffix DFA）的专门用于处理多串匹配的数据结构，其构造方法大致是先构造模板文本的trie树，再通过后缀链接生成包含所有转移的trie图。参考源代码如下：
（此代码从控制台读入一个最大支持到1000×1000的字符矩阵，以及最多1000个文本，程序向控制台输出每一个文本在矩阵中的起始位置和方向，以A-H表示八个方向，在Intel Pentium D 2.1G的处理器上对于任何数据均可在1s内完成运算)

#include <stdio.h>
#include <string.h>
int n,m,l,totalnode;
#define N 1100
#define M 1100000
char data[N][N];
char word[N];
typedef struct

int suffix,kind;
int c[26];
trieT;
trieT trie[M];
typedef struct

int a,b;
char oper;
ans_type;
ans_type ans[N];
int Q[M];
char nowoper;
const int thitah[8]=1,1,0,-1,-1,-1,0,1;
const int thital[8]=0,-1,-1,-1,0,1,1,1;

void read_data()

scanf("%d %d %d%*c",&n,&m,&l);
int i,j;
for (i=1;i<=n;i++)

for (j=1;j<=m;j++) scanf("%c",&data[i][j]);data[i][j]-='A';
scanf("%*c");


void insert(int s,int len)

int i,pnt=1;
for (i=len-1;i>=0;i--)

if (trie[pnt].c[word[i]]!=0) pnt=trie[pnt].c[word[i]];
else

totalnode++;
trie[pnt].c[word[i]]=totalnode;
pnt=totalnode;
trie[pnt].kind=-1;trie[pnt].suffix=0;
memset(trie[pnt].c,0,sizeof(trie[pnt].c));


trie[pnt].kind=s;

void init()

totalnode=1;
trie[1].kind=-1;trie[1].suffix=1;
memset(trie[1].c,0,sizeof(trie[1].c));
int i,j,len;
for (i=1;i<=l;i++)

scanf("%s",&word);
len=strlen(word);
for (j=0;j<len;j++) word[j]-='A';
insert(i,len);


void make_trie_graph()

int i,temp,tempnode,cl,op;
cl=0;op=0;
for (i=0;i<26;i++) if (trie[1].c[i]!=0)

temp=trie[1].c[i];
trie[temp].suffix=1;
if (trie[temp].kind==-1) trie[temp].kind=trie[1].kind;
Q[++op]=temp;
else trie[1].c[i]=1;
while (cl<op)

tempnode=Q[++cl];
for (i=0;i<26;i++) if (trie[tempnode].c[i]!=0)

temp=trie[tempnode].c[i];
trie[temp].suffix=trie[trie[tempnode].suffix].c[i];
if (trie[temp].kind==-1) trie[temp].kind=trie[trie[temp].suffix].kind;
Q[++op]=temp;
else trie[tempnode].c[i]=trie[trie[tempnode].suffix].c[i];


void get_ans(int s,int h,int l)

while (trie[s].kind!=-1)

ans[trie[s].kind].a=h;ans[trie[s].kind].b=l;
ans[trie[s].kind].oper=nowoper;
s=trie[s].suffix;


void check(int h,int l)

int pnt=1;
while ((h>0) && (h<=n) && (l>0) && (l<=m))

pnt=trie[pnt].c[data[h][l]];
if (trie[pnt].kind!=-1) get_ans(pnt,h,l);
h+=thitah[nowoper];l+=thital[nowoper];


void work_ans()

int i;
nowoper=0;for (i=1;i<=m;i++) check(1,i);
nowoper=1;for (i=1;i<=m;i++) check(1,i);for (i=2;i<=n;i++) check(i,m);
nowoper=2;for (i=1;i<=n;i++) check(i,m);
nowoper=3;for (i=1;i<=n;i++) check(i,m);for (i=1;i<m;i++) check(n,i);
nowoper=4;for (i=1;i<=m;i++) check(n,i);
nowoper=5;for (i=1;i<=m;i++) check(n,i);for (i=1;i<n;i++) check(i,1);
nowoper=6;for (i=1;i<=n;i++) check(i,1);
nowoper=7;for (i=1;i<=n;i++) check(i,1);for (i=2;i<=m;i++) check(1,i);


void show_ans()

int i;
for (i=1;i<=l;i++) printf("%d %d %c\n",ans[i].a-1,ans[i].b-1,ans[i].oper+'A');


int main()

read_data();
init();
make_trie_graph();
work_ans();
show_ans();
return 0;


若楼主希望学习trie图的具体理论和构造方法，可回帖注明。 参考技术A 你的问题,我还是不太明白,我写了一个简单,但只是针对,你上面的那个,没什么扩展性,你先看看,坐标呢,直接打印,没有写入文件..

#include"T1.h"
#include<iostream>
using namespace std;
const void Sevch(int (&Sj)[6][9],int (&key)[5]);
int main(int argc,char* argv[])

int Array[6][9]=

1,1,4,1,1,4,1,1,0,
4,1,1,0,0,0,1,4,0,
4,0,0,1,1,4,4,1,0,
0,0,0,0,0,1,0,1,0,
0,0,1,1,4,1,1,1,0,
0,0,0,0,4,0,0,0,0,
;
int Key[5]=1,1,4,1,1;
Sevch(Array,Key);
cin.get();

const void Sevch(int (&Sj)[6][9],int (&key)[5])

int Len=6;
int Lie=9;
for(int i=0;i<Len;i++)

for(int j=0;j<Lie;j++)

if(Sj[i][j]==key[0]&&Sj[i][j+1]==key[1]&&Sj[i][j+2]==key[2]&&Sj[i][j+3]==key[3]&&Sj[i][j+4]==key[4])

cout<<"Key:"<<"在"<<i+1<<"行"<<j+1<<"列"<<endl;





V1.1增强版.

#include<iostream>
using namespace std;
const void Sevch_R(int (&Sj)[6][9],int (&key)[5]); //水平方向查找.
const void Secvh_X(int (&Sj)[6][9],int (&key)[5]); //垂直方向查找.
int main(int argc,char* argv[])

int Array[6][9]=

1,1,4,1,1,1,4,1,1,
1,1,1,1,1,1,4,1,1,
4,4,4,1,1,4,4,1,1,
1,1,1,4,1,1,0,1,4,
1,1,1,1,4,1,1,1,1,
1,1,4,1,1,1,4,1,1,
;
int Key[5]=1,1,4,1,1;
cout<<"水平方向的Key有:\n";
Sevch_R(Array,Key);
cout<<"\n垂直方向的Key有:\n";
Secvh_X(Array,Key);
cin.get();


const void Sevch_R(int (&Sj)[6][9],int (&key)[5])

for(int i=0;i<6;i++)

for(int j=0;j<5;j++)

if(Sj[i][j]==key[0]&&Sj[i][j+1]==key[1]&&Sj[i][j+2]==key[2]&&Sj[i][j+3]==key[3]&&Sj[i][j+4]==key[4])

cout<<"Key:"<<"在"<<i+1<<"行"<<j+1<<"列"<<endl;





const void Secvh_X(int (&Sj)[6][9],int (&key)[5])

for(int j=0;j<2;j++)

for(int i=0;i<9;i++)

if(Sj[j][i]==key[0]&&Sj[j+1][i]==key[1]&&Sj[j+2][i]==key[2]&&Sj[j+3][i]==key[3]&&Sj[j+4][i]==key[4])

cout<<"Key:"<<"在"<<j+1<<"行"<<i+1<<"列"<<endl;



参考技术B 修改后，横纵方向各扫一遍
#include <iostream>
using namespace std;
int Array[6][9] =

1,1,0,1,0,0,1,0,0,
4,1,1,0,0,0,1,4,0,
4,0,0,1,1,4,4,1,0,
0,0,0,0,0,1,0,1,0,
0,0,1,1,4,1,0,1,0,
0,0,0,0,4,0,0,0,0,
;
int arrayString[]=1,1,4,0,0;
int main(void)

int y=sizeof(*Array)/sizeof(int);
int x=sizeof(Array)/sizeof(int)/y;
int len=sizeof(arrayString)/sizeof(int);
int i,j,k;
for(i=0;i<x;i++)
for(j=0;j<y-len;j++)
for(k=0;k<len;k++)
if(Array[i][j+k]!=arrayString[k])break;

if(k==len)
cout<<"x="<<j+1<<"y="<<i+1<<endl;


for(i=0;i<x-len;i++)
for(j=0;j<y;j++)
for(k=0;k<len;k++)
if(Array[i+k][j]!=arrayString[k])break;

if(k==len)
cout<<"x="<<j+1<<"y="<<i+1<<endl;


return 0;
参考技术C 只要横向的一组数里面是1，1，4，1，1就行吗？

算法零基础学习关于数组的一些练习题| leetcode 202218861260的题解

2022. 将一维数组转变成二维数组

问题描述：

给你一个下标从 0 开始的一维整数数组 original 和两个整数 m 和 n 。你需要使用 original 中 所有 元素创建一个 m 行 n 列的二维数组。

original 中下标从 0 到 n - 1 （都 包含 ）的元素构成二维数组的第一行，下标从 n 到 2 * n - 1 （都 包含 ）的元素构成二维数组的第二行，依此类推。

请你根据上述过程返回一个 m x n 的二维数组。如果无法构成这样的二维数组，请你返回一个空的二维数组。

提示：

    1 <= original.length <= 5 * 104
    1 <= original[i] <= 105
    1 <= m, n <= 4 * 104

思路分析

简单来讲，这道题就是将一个一维数组转换为一个m * n的二维数组。如下：

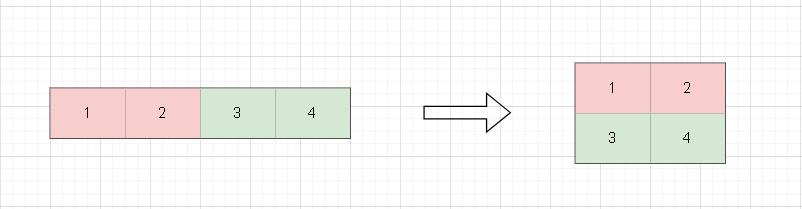
因此，解决这个问题关键在于如何将一维数组的索引正确地转换为二维数组的索引。

代码：

    class Solution 
        public int[][] construct2DArray(int[] original, int m, int n) 
            int[][] res = ;
            int k = 0;
            if(original.length != m * n)
                return res;
            
            res  = new int[m][n];
            for(int i = 0; i < m; i++)
                for(int j = 0; j < n; j++)
                    res[i][j] = original[k++];
                
            
            return res;
        
    

1886. 判断矩阵经轮转后是否一致

问题描述：

给你两个大小为 n x n 的二进制矩阵 mat 和 target 。现 以 90 度顺时针轮转 矩阵 mat 中的元素 若干次 ，如果能够使 mat 与 target 一致，返回 true ；否则，返回 false 。

提示：

n == mat.length == target.length
n == mat[i].length == target[i].length
1 <= n <= 10
mat[i][j] 和 target[i][j] 不是 0 就是 1

思路分析

最简单的方法就是『将mat矩阵一次次的旋转，看一下是否能与target一致』。

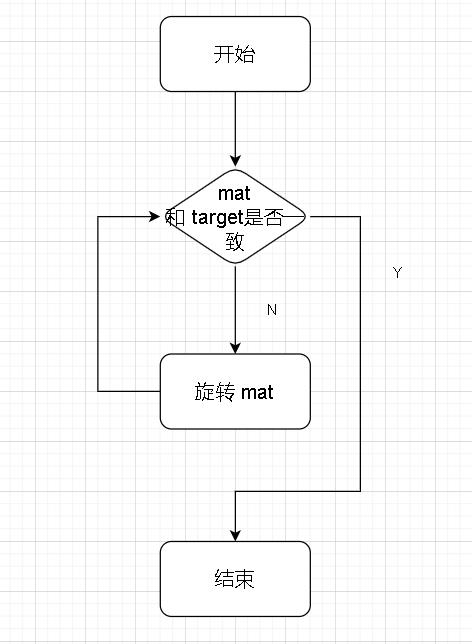
看下面这个例子：
这里对 Mat 进行若干次旋转，并判断 Mat 和 target 是否一致。
在经过两次旋转之后，Mat 将和 target 一致。
由于mat矩阵每次都是旋转90°，所以，在最多旋转两次。（第三次旋转将和原矩阵一样）

代码：

    class Solution 
        public boolean findRotation(int[][] mat, int[][] target) 
            int i = 0;
            while(i < 4)
                if(equal(mat,target,mat.length))
                    return true;
                mat = rotate(mat);
                i++;
            
            return false;
        
     
        // 轮转矩阵
        int[][] rotate(int[][] mat)
            int length = mat.length;
            for(int i = 0; i < length / 2; i++)
                for(int j = 0; j < length; j++)
                    int s = mat[i][j];
                    mat[i][j] = mat[length - 1 - i][j];
                    mat[length - 1 -i][j] = s;
                
            
            for(int i = 0; i < length; i++)
                for(int j = i; j < length; j++)
                    int s = mat[i][j];
                    mat[i][j] = mat[j][i];
                    mat[j][i] = s;
                
            
            return mat;
        
     
        // 比较相等
        boolean equal(int[][] mat, int[][] target, int length)
            for(int i = 0; i < length; i++)
                for(int j = 0; j < length; j++)
                    if(mat[i][j] != target[i][j])
                        return false;
                
            
     
            return true;
        
    

1260. 二维网格迁移

问题描述：

给你一个 m 行 n 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。

每次「迁移」操作将会引发下述活动：

位于 grid[i][j] 的元素将会移动到 grid[i][j + 1]。
位于 grid[i][n - 1] 的元素将会移动到 grid[i + 1][0]。
位于 grid[m - 1][n - 1] 的元素将会移动到 grid[0][0]。

请你返回 k 次迁移操作后最终得到的 二维网格。

提示：

m == grid.length
n == grid[i].length
1 <= m <= 50
1 <= n <= 50
-1000 <= grid[i][j] <= 1000
0 <= k <= 100

思路分析：

我们来看一下「迁移」：

1. 位于grid[i][j]的元素移动到grid[i][j + 1]；
   
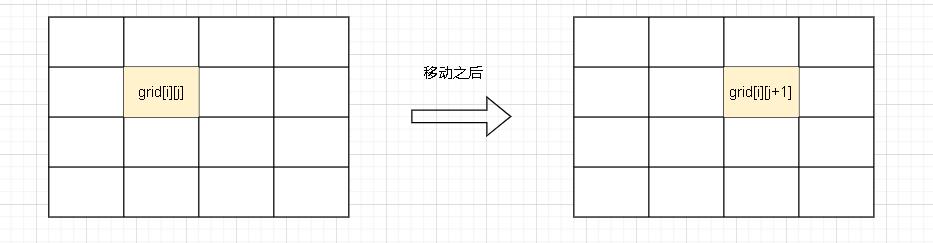
2. 位于 grid[i][n - 1] 的元素将会移动到 grid[i + 1][0];
   
3. 位于 grid[m - 1][n - 1] 的元素将会移动到 grid[0][0]。
   

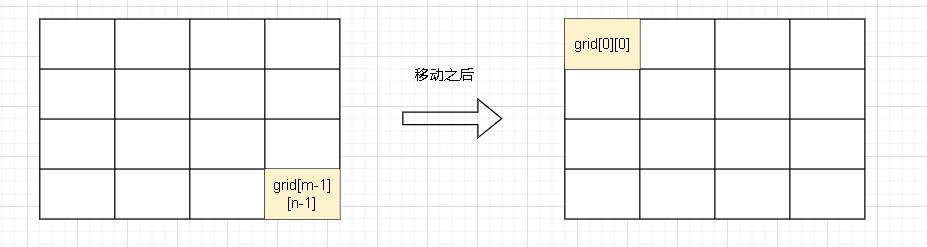
如果我们将它视为一个「一维循环数组」，那么，这里每「迁移一次」，数组的元素就会「后移」一次 。

代码：

    class Solution 
        public List<List<Integer>> shiftGrid(int[][] grid, int k) 
            int row_num = grid.length;
            int col_num = grid[0].length;
            int num = row_num * col_num;
            int[][] res = new int[row_num][col_num];
     
            for(int i = 0; i < row_num; i++)
                for(int j = 0; j < col_num; j++)
                    int location = (j + i * col_num + k) % num;
                    res[location / col_num][location % col_num] = grid[i][j];
                
            
     
            List<List<Integer>> result = new ArrayList<>();
            for (int[] row : res) 
                List<Integer> listRow = new ArrayList<>();
                result.add(listRow);
                for (int v : row) listRow.add(v);
            
     
            return result;