机器学习强基计划1-3：图文详解Logistic回归原理(两种优化)+Python实现

Posted 2022-08-12 Mr.Winter`

目录

• 0 写在前面
• 1 什么是Logistic回归？
• 2 手推Logistic回归原理
• 3 Python实现
• • 3.1 创建分类器
  • 3.2 定义优化过程
  • 3.3 优化函数
  • 3.4 可视化

0 写在前面

机器学习强基计划聚焦深度和广度，加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理；“广”在分析多个机器学习模型：决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。

🚀详情：机器学习强基计划(附几十种经典模型源码合集)

1 什么是Logistic回归？

在机器学习强基计划1-1：图文详解感知机算法原理+Python实现提到广义线性模型(generalized linear model)

$$f\left({\mathbf{x}}^{\left(i\right)}\right)=g^{-1}\left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}+b\right)$$

其中单调可微函数$g\left(\cdot \right)$称为联系函数(link function)。广义线性模型本质上仍是线性的，但通过$g\left(\cdot \right)$进行非线性映射，使之具有更强的拟合能力，类似神经元的激活函数。

Logistic回归是$g^{-1}\left(z\right)=\frac{1}{1+e^{-z}}$时的广义线性模型，$g^{-1}\left(z\right)=\frac{1}{1+e^{-z}}$这个函数在人工智能领域非常著名，称为sigmoid函数，其值被限定在0-1区间内，因此也可认为是概率映射。

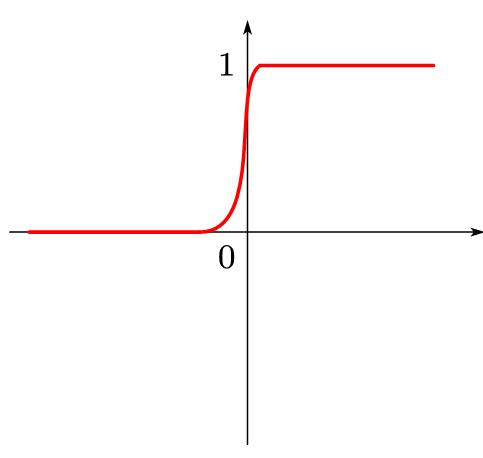
所以Logistic回归可以认为输出了预测类别的概率，因此Logistic回归本质上是在线性回归基础上，将预测值映射到概率区间内的分类学习方法。

常见的Logisitc回归类型如表所示。

Logistic回归分析类型	输出标签举例	说明
二元Logistic回归	是/否	分类数据，且仅分为两类
多元无序Logistic回归	一线城市、二线城市、三线城市	分类数据，分类超过两类且同类别之间没有对比意义
多元有序Logistic回归	不同意、无所谓、同意	分类数据，分类超过两类且同类别之间具有对比意义

本节讨论最简单的二元Logistic回归。

2 手推Logistic回归原理

首先列出Logistic回归的表达式：

$$f\left({\hat{\mathbf{x}}}^{\left(i\right)}\right)=g^{-1}\left({\hat{\mathbf{w}}}^T{\hat{\mathbf{x}}}^{\left(i\right)}\right)\iff {\hat{\mathbf{w}}}^T{\hat{\mathbf{x}}}^{\left(i\right)}=\ln \frac{f\left({\hat{\mathbf{x}}}^{\left(i\right)}\right)}{1-f\left({\hat{\mathbf{x}}}^{\left(i\right)}\right)}$$

可将输出$f\left({\hat{\mathbf{x}}}^{\left(i\right)}\right)$视为给定一个训练样本${\hat{\mathbf{x}}}^{\left(i\right)}$输出预测类别的后验概率$p\left(y_i=1|{\hat{\mathbf{x}}}^{\left(i\right)}\right)$。

这里涉及一些概率论方面的知识，关于概率、似然等概念请参考机器学习强基计划4-1：你真的分得清频率、概率、几率和似然吗？

接下来根据极大似然法估计参数向量$\hat{\mathbf{w}}$，即获得在给定观测样本的条件下，最接近样本真实标签的参数组合，令损失函数$E\left(\hat{\mathbf{w}}\right)={\sum }_{i=1}^m\ln p\left(y_i|{\hat{\mathbf{x}}}^{\left(i\right)};\hat{\mathbf{w}}\right)$，考虑二分类情形：

p ( y i = 1 ∣ x ^ ( i ) ; w ^ ) = y i p ( y i = 1 ∣ x ^ ( i ) ; w ^ ) p ( y i = 0 ∣ x ^ ( i ) ; w ^ ) = ( 1 − y i ) p ( y i = 0 ∣ x ^ ( i ) ; w ^ ) ⇒ E ( w ^ ) = ∑ i = 1 m y i ln ⁡ p ( y i = 1 ∣ x ^ ( i ) ; w ^ ) + ( 1 − y i ) ln ⁡ ( 1 − p ( y i = 1 ∣ x ^ ( i ) ; w ^ ) ) \\begincases p\\left( y_i=1|\\boldsymbol\\hatx^\\left( i \\right);\\boldsymbol\\hatw \\right) =y_ip\\left( y_i=1|\\boldsymbol\\hatx^\\left( i \\right);\\boldsymbol\\hatw \\right)\\\\ p\\left( y_i=0|\\boldsymbol\\hatx^\\left( i \\right);\\boldsymbol\\hatw \\right) =\\left( 1-y_i \\right) p\\left( y_i=0|\\boldsymbol\\hatx^\\left( i \\right);\\boldsymbol\\hatw \\right)\\\\\\endcases\\\\\\Rightarrow E\\left( \\boldsymbol\\hatw \\right) =\\sum_i=1^my_i\\ln p\\left( y_i=1|\\boldsymbol\\hatx^\\left( i \\right);\\boldsymbol\\hatw \\right) +\\left( 1-y_i \\right) \\ln \\left( 1-p\\left( y_i=1|\\boldsymbol\\hatx^\\left( i \\right);\\boldsymbol\\hatw \\right) \\right) ⎩ ⎨ ⎧​p(yi​=1∣x^(i);w^)=yi​p(yi​=1∣x^(i);w^)p(yi​=0∣以上是关于机器学习强基计划1-3：图文详解Logistic回归原理(两种优化)+Python实现的主要内容，如果未能解决你的问题，请参考以下文章

机器学习强基计划5-4：图文详解影响流动与有向分离(D-分离)(附Python实现)

机器学习强基计划7-2：图文详解K-均值聚类(K-means)算法(附Python实现)

机器学习强基计划4-3：详解朴素贝叶斯分类原理(附例题+Python实现)

机器学习强基计划0-2：什么是机器学习？和AI有什么关系？

机器学习强基计划8-1：图解主成分分析PCA算法(附Python实现)

机器学习强基计划0-1：教程导读