机器学习随机森林AdaBoostGBDTXGBoost从零开始理解
Posted Better Bench
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习随机森林AdaBoostGBDTXGBoost从零开始理解相关的知识,希望对你有一定的参考价值。

1 相关概念
1.1 信息熵
信息熵时用来哦衡量信息不确定性的指标,不确定性时一个时间出现不同结果的可能性。
H
(
x
)
=
−
∑
i
=
1
n
P
(
X
=
i
)
l
o
g
2
P
(
X
=
i
)
H(x) = -\\sum_i=1^n P(X=i)log_2P(X=i)
H(x)=−i=1∑nP(X=i)log2P(X=i)
其中:P(X=i)为随机变量x取值为i的概率
1.2 条件熵
条件熵:再给定随机变量Y的条件下,随机变量X的不确定性
H
(
X
∣
Y
=
v
)
=
−
∑
i
=
1
n
P
(
X
=
i
∣
Y
=
v
)
l
o
g
2
P
(
X
=
i
∣
Y
=
v
)
H(X|Y=v) = -\\sum_i=1^nP(X=i|Y=v)log_2P(X=i|Y=v)
H(X∣Y=v)=−i=1∑nP(X=i∣Y=v)log2P(X=i∣Y=v)
1.3 信息增益
信息增益:熵-条件熵。代表了在一个条件下,信息不确定性减少的程度。
I
(
X
,
Y
)
=
H
(
X
)
−
H
(
X
∣
Y
)
I(X,Y) = H(X)-H(X|Y)
I(X,Y)=H(X)−H(X∣Y)
1.4 基尼指数
基尼指数:又称为Gini不纯度,表示在样本集合中一个随机选中的样本杯分错的概率。
注意:Gini指数越小表示集合中被选中的样本被分错的概率越小,也就说集合的纯度越高,反之,集合越不纯。当集合中所有样本为一个类时,基尼指数为0。
G
i
n
i
(
p
)
=
∑
k
=
1
K
p
k
(
1
−
p
k
)
=
1
−
∑
k
=
1
K
p
k
Gini(p)= \\sum_k=1^Kp_k(1-p_k) = 1-\\sum_k=1^Kp_k
Gini(p)=k=1∑Kpk(1−pk)=1−k=1∑Kpk
其中pk表示选中的样本属于第k个类别的概率。
1.5 集成学习
集成学习是通过构建并组合多个学习器来完成学习任务的算法,集成学习常用的有两类:
Bagging:基学习器之间无强依赖关系,可同时生成的并行化方法
Boosting:基学习器之间存在强烈的依赖关系,必须穿行生成基分类器的方法

(1)Bagging(Bootstrap Aggregating)算法
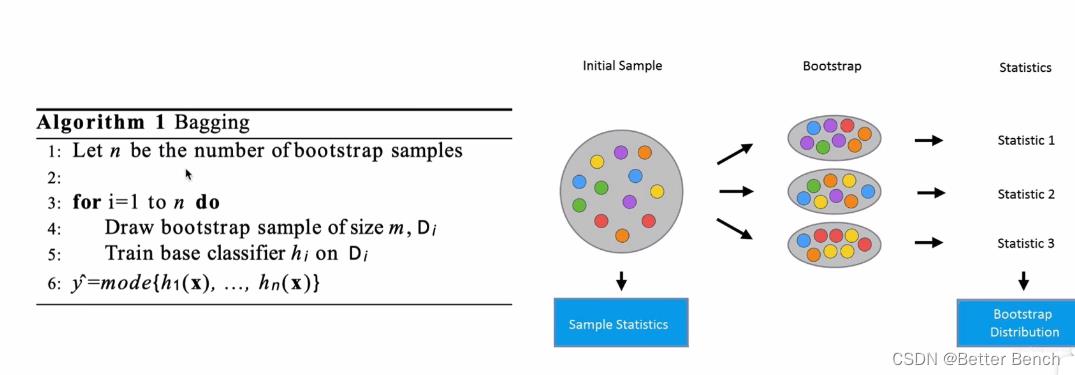
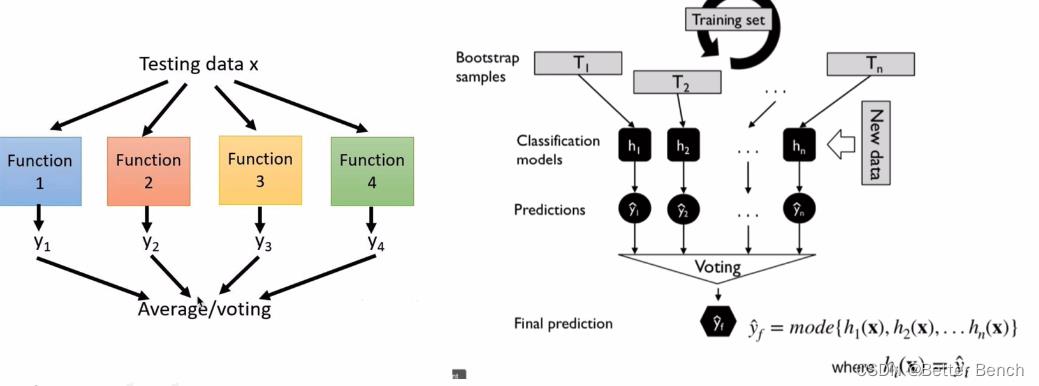
N个弱学习器,每个学习器的训练数据,来自于原始数据中的随机采样的部分数据。训练模型后,预测新数据。在分类问题中,选择多N个学习器的预测结果中的众数(即,投票方法)作为最终的预测结果。在回归问题中,选择多N个学习器的预测结果中的平均值作为最终的预测结果。
(2)Boosting算法
是将弱学算法提升为强学习算法的过程,通过反复学习得到一系列弱分类器(决策树和逻辑回归)组合这些弱分类器得到一个强分类器。Boosting算法要涉及到两个部分,加法模型和前向分布算法。
加法模型:强分类器由一系列弱分类器线性相加而成。一般组合形式如下:
F
M
(
x
:
P
)
=
∑
m
=
1
n
β
m
h
(
x
;
a
m
)
F_M(x:P) = \\sum_m=1^n\\beta_mh(x;a_m)
FM(x:P)=m=1∑nβmh(x;am)
其中 h ( x ; a M ) h(x;a_M) h(x;aM)是弱分类器, a m a_m am是弱分类器学习到的最优参数, β m \\beta_m βm是弱学习在强分类器中所占比重,P是所有 a m a_m am和 β m \\beta_m βm的组合。这些弱分类器线性相加组成强分类器。
前向分步:在训练过程中,下一轮迭代产生的分类器是在上一轮的基础上训练得来的。
F
m
(
x
)
=
F
m
−
1
(
x
)
+
β
m
h
m
(
x
;
a
m
)
F_m(x) = F_m-1(x)+\\beta_mh_m(x;a_m)
Fm(x)=Fm−1(x)+βmhm(x;am)
2 随机森林
(1)概念
随机森林 = Bagging+决策树
同时训练多个决策树,预测试综合考虑多个结果进行预测,例如取多个节点的均值(回归问题),或者众数(分类)。
(2)优缺点
优点
- 它可以出来很高维度(特征很多)的数据,并且不用降维,无需做特征选择
- 它可以判断特征的重要程度
- 可以判断出不同特征之间的相互影响
- 消除了决策树容易过拟合的缺点
- 减小了预测的方差,预测值不会因训练数据的小变化而剧烈变化
- 训练速度比较快,容易做成并行方法
- 实现起来比较简单
- 对于不平衡的数据集来说,它可以平衡误差。
- 如果有很大一部分的特征遗失,仍可以维持准确度。
缺点
- 随机森林已经被证明在某些噪音较大的分类或回归问题上会过拟合。
- 对于有不同取值的属性的数据,取值划分较多的属性会对随机森林产生更大的影响,所以随机森林在这种数据上产出的属性权值是不可信的
(3)随机性体现在两点
- 从原来是训练数据集随机(带放回Boostrap)取一个子集,作为森林中某一个决策树的训练数据集
- 每一次选择分叉的特征时,限定为在随机选择的特征的子集中寻找一个特征
3 AdaBoost
(1)概念
AdaBoost的思想时将关注点放在被错误分类的样本上,减小上一轮被正确分类的样本权值,提高被错误分类的样本权值。
Adaboost采用加权投票的方法,分类误差小的弱分类器的权重大,而分类误差大的弱分类器的权重小。
(2)算法过程
假设输入的训练数据为:
T
=
(
x
1
,
y
1
)
,
(
x
1
,
y
1
)
,
.
.
.
,
(
x
N
,
y
N
)
x
i
∈
X
⊆
R
n
,
y
i
∈
Y
=
−
1
,
1
T = \\(x_1,y_1),(x_1,y_1),...,(x_N,y_N)\\\\\\ x_i \\in X \\subseteq R^n,y_i \\in Y = \\-1,1\\
T=(x1,y1),(x1,y1),...,(xN,yN)xi∈X⊆Rn,yi∈Y=−1,1
迭代次数即弱分类器个数M
-
初始化训练样本的权值分布为
D 1 = ( w 1 , 1 , w 1 , 2 , . . . , w 1 , i ) = 1 N , i = 1 , 2 , . . , N D_1 = (w_1,1,w_1,2,...,w_1,i) = \\frac1N,i=1,2,..,N D1=(w1,1,w1,2,...,w1,i)=N1,i=1,2,..,N -
对于m = 1,2,…,M
(a)使用具有权值分布 D m D_m Dm的训练数据集进行学习,得到弱分类器 G m ( x ) G_m(x) Gm(x)
(b)计算 G m ( x ) G_m(x) Gm(x)在训练集上的分类误差率
e m = ∑ i = 1 N w m , i I ( G m ( x i ) ≠ y i ) e_m = \\sum_i=1^Nw_m,iI(G_m(x_i) \\not = y_i) em=i=1∑Nw以上是关于机器学习随机森林AdaBoostGBDTXGBoost从零开始理解的主要内容,如果未能解决你的问题,请参考以下文章