计算机视觉算法——DETR / Deformable DETR / DETR 3D

Posted 2022-08-10 Leo-Peng

计算机视觉算法——DETR / Deformable DETR / DETR 3D

• 计算机视觉算法——DETR / Deformable DETR / DETR 3D
• • 1. DETR
  • • 1.1 Transformer Encoder-Decoder
    • 1.2 Set-to-Set Loss
    • 1.3 Positional Embedding
  • 2. Deformable DETR
  • • 2.1 Deformable Attention Module
    • 2.2 Deformable Transformer Encoder-Decoder
    • 2.3 Conclusion
  • 3. DETR3D
  • • 3.1 2D to 3D Transfomer

计算机视觉算法——DETR / Deformable DETR / DETR 3D

DETR是DEtection TRansformer的缩写，该方法发表于2020年ECCV，原论文名为《End-to-End Object Detection with Transformers》。

传统的目标检测是基于Proposal、Anchor或者None Anchor的方法，并且至少需要非极大值抑制来对网络输出的结果进行后处理，涉及到复杂的调参过程。而DETR使用了Transformer Encoder-Decoder的结构，并且通过集合预测损失实现了真正意义上的端到端的目标检测方法。Transformer Encoder-Decoder是怎么实现的？集合预测损失是什么？后文具体介绍。

对于目标检测方向不是很了解的同学可以参考计算机视觉算法——目标检测网络总结。

1. DETR

DETR网络结构如下图所示：

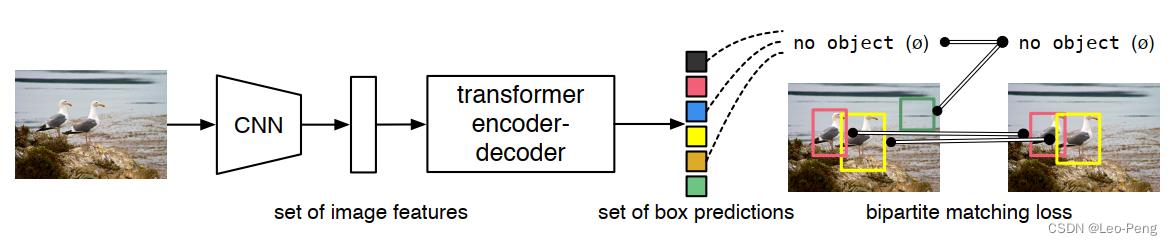
首先第一步是通过一个CNN对输入图片抽取特征，然后将特征图拉直输入Transformer Encoder-Decoder。第二步的Transformer Encoder部分就是使得网络更好地去学习全局的特征；第三步使用Transformer Decoder以及Object Query从特征中学习要检测的物体；第四步就是将Object Query的结果和真值进行二分图匹配（Set-to-Set Loss），最后在匹配上的结果上计算分类Loss和位置回归Loss。

以上是训练的基本过程，推理过程唯一的区别就是在第四步，第四步通过对Object Query设置一个阈值来输出最终检测的结果，这个结果不再需要进行进行任何后处理，而是直接作为最终的输出。

下面我们结合代码具体展开Transformer Encoder-Decoder和Set-to-Set Loss的细节：

1.1 Transformer Encoder-Decoder

Transformer Encoder-Decoder结构如下图所示，其中红色注释为输入为$3\times 800\times 1066$大小的图片后各个步骤Feature大小。

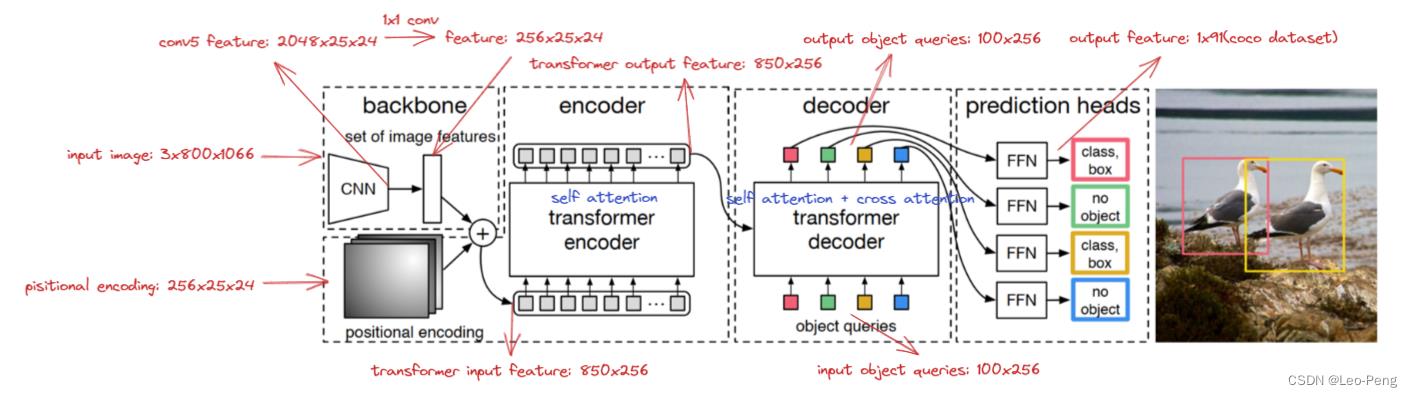
Transformer Encoder-Decoder的forward函数如下：

def forward(self, src, mask, query_embed, pos_embed):
        # flatten NxCxHxW to HWxNxC
        bs, c, h, w = src.shape
        src = src.flatten(2).permute(2, 0, 1)
        pos_embed = pos_embed.flatten(2).permute(2, 0, 1)
        query_embed = query_embed.unsqueeze(1).repeat(1, bs, 1)
        mask = mask.flatten(1)

        tgt = torch.zeros_like(query_embed)
        memory = self.encoder(src, src_key_padding_mask=mask, pos=pos_embed)
        hs = self.decoder(tgt, memory, memory_key_padding_mask=mask,
                          pos=pos_embed, query_pos=query_embed)
        return hs.transpose(1, 2), memory.permute(1, 2, 0).view(bs, c, h, w)

其中
src为Backbone抽取后的特征，输入Encoder前需要先对其进行展平处理；
pos_embed为位置编码，在DETR中位置编码是一个值固定的位置编码，具体参见下文有1.3中的介绍；
query_embed是一个可学习的位置编码，也就是上文体到的Object Query，其作用在Decoder中就是通过Encoder后的Feature和query_embed不断做Cross Attention，最query_embed的每一维就是一个检测结果的输出;
mask是DETR为了兼容不同分辨率图像作为输入，会在输入时将不同分别的图像Zero Padding成固定分辨率，Zero Padding部分不包含任何信息，因此不能用来计算Attention，因此作者在这里保留将Zero Padding部分传入了src_key_padding_mask。

接下来的Encoder-Decoder部分和《Attention is All You Need》中几乎一致，Encoder层结构如下图所示：
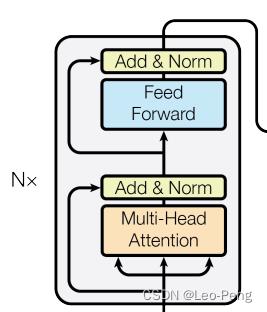代码如下：

def forward_post(self,
                 src,
                 src_mask: Optional[Tensor] = None,
                 src_key_padding_mask: Optional[Tensor] = None,
                 pos: Optional[Tensor] = None):
    q = k = self.with_pos_embed(src, pos)
    src2 = self.self_attn(q, k, value=src, attn_mask=src_mask,
                          key_padding_mask=src_key_padding_mask)[0]
    src = src + self.dropout1(src2)
    src = self.norm1(src)
    src2 = self.linear2(self.dropout(self.activation(self.linear1(src))))
    src = src + self.dropout2(src2)
    src = self.norm2(src)
    return src

Decoder结构如下图所示：
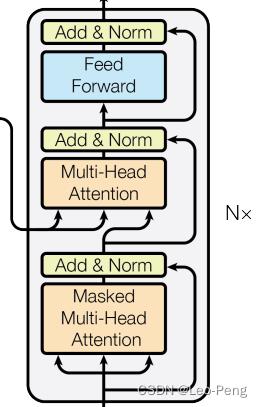代码如下：

def forward_post(self, tgt, memory,
                 tgt_mask: Optional[Tensor] = None,
                 memory_mask: Optional[Tensor] = None,
                 tgt_key_padding_mask: Optional[Tensor] = None,
                 memory_key_padding_mask: Optional[Tensor] = None,
                 pos: Optional[Tensor] = None,
                 query_pos: Optional[Tensor] = None):
    q = k = self.with_pos_embed(tgt, query_pos)
    tgt2 = self.self_attn(q, k, value=tgt, attn_mask=tgt_mask,
                          key_padding_mask=tgt_key_padding_mask)[0]
    tgt = tgt + self.dropout1(tgt2)
    tgt = self.norm1(tgt)
    tgt2 = self.multihead_attn(query=self.with_pos_embed(tgt, query_pos),
                               key=self.with_pos_embed(memory, pos),
                               value=memory, attn_mask=memory_mask,
                               key_padding_mask=memory_key_padding_mask)[0]
    tgt = tgt + self.dropout2(tgt2)
    tgt = self.norm2(tgt)
    tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt))))
    tgt = tgt + self.dropout3(tgt2)
    tgt = self.norm3(tgt)
    return tgt

这里有个细节，除了第一层之外，query_embed在做Cross Attention之前，都需必须要做一次Self Attention，Self-Attention各个Query了解其他Query掌握的信息。

最后总结下，Transformer Encoder-Decoder有什么好处呢？
我觉得Transformer Encoder-Decoder应该是Set-to-Set成功的原因之一，在DETR之前其实也有一些文章提出Set-to-Set的想法，但是由于网络使用的Backbone不够强，因此并没有取得很好的效果。而Transformer Encoder-Decoder学习的是全局的特征，它可以使得其中某一个特征与全局里的其他特征都有了交互，网络就能更加清楚的知道哪里是一个物体，哪里是另外一个物体，一个物体应该就是对应一个输出，这也就更加符合Set-to-Set的假设。

1.2 Set-to-Set Loss

所谓Set-to-Set Loss就是将在计算网络损失前加一个二分图匹配的过程，使得最后预测结果只和匹配上的真值计算损失，如下公式所示：$$\hat{\sigma }=\underset{\sigma \in {\mathfrak{S}}_N}{\mathrm{argmin}}\sum _i^N{\mathcal{L}}_{\mathrm{match}}\left(y_i,{\hat{y}}_{\sigma (i)}\right)$$其中$y_i$为真值，${\hat{y}}_{\sigma (i)}$为预测值，${\mathcal{L}}_{\mathrm{match}}$为二分图匹配算法，对二分图匹配不熟悉的同学可以参考视觉SLAM总结——SuperPoint / SuperGlue中的介绍，区别是，在DETR代码码实现中调用的是scipy库中的linear_sum_assignment函数，该函数输入一个$M\times N$大小的Cost矩阵能计算$M$和$N$之间的匹配关系，在DETR中Cost矩阵由分类损失${\hat{p}}_{\sigma (i)}\left(c_i\right)$和Box损失${\mathcal{L}}_{\mathrm{box}}\left(b_i,{\hat{b}}_{\sigma (i)}\right)$两部分构成，分类损失为负的Softmax后的概率，Box损失为L1损失和Generalized IOU损失两部分构成如下：

def forward(self, outputs, targets):
        """ Performs the matching

        Params:
            outputs: This is a dict that contains at least these entries:
                 "pred_logits": Tensor of dim [batch_size, num_queries, num_classes] with the classification logits
                 "pred_boxes": Tensor of dim [batch_size, num_queries, 4] with the predicted box coordinates

            targets: This is a list of targets (len(targets) = batch_size), where each target is a dict containing:
                 "labels": Tensor of dim [num_target_boxes] (where num_target_boxes is the number of ground-truth
                           objects in the target) containing the class labels
                 "boxes": Tensor of dim [num_target_boxes, 4] containing the target box coordinates

        Returns:
            A list of size batch_size, containing tuples of (index_i, index_j) where:
                - index_i is the indices of the selected predictions (in order)
                - index_j is the indices of the corresponding selected targets (in order)
            For each batch element, it holds:
                len(index_i) = len(index_j) = min(num_queries, num_target_boxes)
        """
        bs, num_queries = outputs["pred_logits"].shape[:2]

        # We flatten to compute the cost matrices in a batch
        out_prob = outputs["pred_logits"].flatten(0, 1).softmax(-1)  # [batch_size * num_queries, num_classes]
        out_bbox = outputs["pred_boxes"].flatten(0, 1)  # [batch_size * num_queries, 4]

        # Also concat the target labels and boxes
        tgt_ids = torch.cat([v["labels"] for v in targets])
        tgt_bbox = torch.cat([v["boxes"] for v in targets])

        # Compute the classification cost. Contrary to the loss, we don't use the NLL,
        # but approximate it in 1 - proba[target class].
        # The 1 is a constant that doesn't change the matching, it can be ommitted.
        cost_class = -out_prob[:, tgt_ids]

        # Compute the L1 cost between boxes
        cost_bbox = torch.cdist(out_bbox, tgt_bbox, p=1)

        # Compute the giou cost betwen boxes
        cost_giou = -generalized_box_iou(box_cxcywh_to_xyxy(out_bbox), box_cxcywh_to_xyxy(tgt_bbox))

        # Final cost matrix
        C = self.cost_bbox * cost_bbox + self.cost_class * cost_class + self.cost_giou * cost_giou
        C = C.view(bs, num_queries, -1).cpu()

        sizes = [len(v["boxes"]) for v in targets]
        indices = [linear_sum_assignment(c[i]) for i, c in enumerate(C.split(sizes, -1))]
        return [(torch.as_tensor(i, dtype=torch.int64), torch.as_tensor(j, dtype=torch.int64)) for i, j in indices]

在求得匹配结果$\hat{\sigma }$后最终的损失大小为： L Hungarian  ( y , y ^ ) = ∑ i = 1 N [ − log ⁡ p ^ σ ^ ( i ) ( c i ) + 1 c i ≠ ∅ L b o x ( b i , b ^ σ ^ ( i ) ) ] \\mathcalL_\\text Hungarian (y, \\haty)=\\sum_i=1^N\\left[-\\log \\hatp_\\hat\\sigma(i)\\left(c_i\\right)+\\mathbb1_\\left\\c_i \\neq \\varnothing\\right\\ \\mathcalL_\\mathrmbox\\left(b_i, \\hatb_\\hat\\sigma(i)\\right)\\right] LHungarian ​(y,y^​)=i=1∑N​[−logp^​σ^(i)​(ci​)+1ci​=∅​Lbox​(bi​,b^以上是关于计算机视觉算法——DETR / Deformable DETR / DETR 3D的主要内容，如果未能解决你的问题，请参考以下文章

计算机视觉算法——基于Transformer的目标检测（DETR / Deformable DETR / DETR 3D）

OW-DETR | 基于 Transformer 的开放世界目标检测器

Vit社区开放麦#38 目标检测新范式！DETR 系列算法解读 - 知识点目录

[深度学习][原创][课程]DETR训练自己的目标检测数据集ubuntu版

JAX 是 Google 开发的计算机视觉研究

如何用DETR（detection transformer）训练自己的数据集