数据结构学习笔记——哈夫曼树
Posted 晚风(●•σ )
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构学习笔记——哈夫曼树相关的知识,希望对你有一定的参考价值。
目录
一、路径、路径长度、权值
1、路径和路径长度
- 在树中,一个结点和另一个结点之间的分支即为这两个结点之间的
路径;路径长度即为树中路径上的分支数目,即路径上所经过的边的个数。 树的路径长度等于根结点到树中每个结点的路径长度之和。
2、权值
- 为树中每个叶子结点(度为1的结点)赋予一个数值,则该值称为
叶子结点的权值,简称为权。
3、带权路径长度
(1)叶子结点的带权路径长度
- 叶子结点的权值与树的根结点到该叶子结点之间的路径长度的乘积称为
叶子结点的带权路径长度。
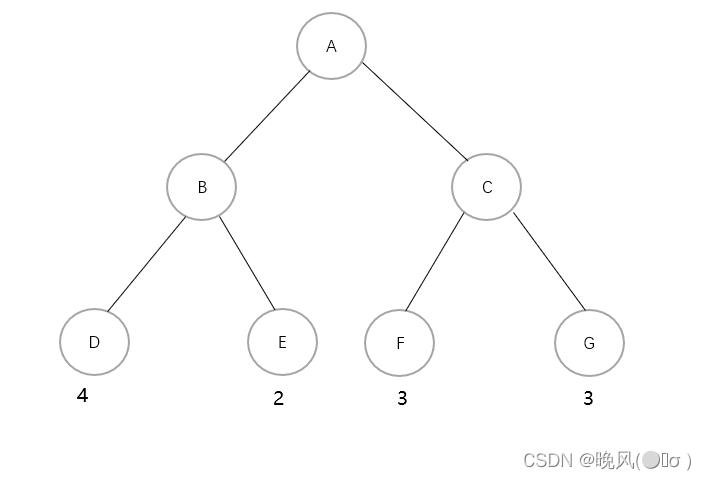
例如上图二叉树中,叶子结点D的权值为4,根结点A到结点D的分支数目为2,所以该叶子结点的带权路径长度为4×2=8。
(2)树的带权路径长度(WPL)
- 树中所有叶子结点的权值乘以该结点的路径长度之和即为
树的带权路径长度(WPL)。
例如上图二叉树中,该二叉树的带权路径长度为:
WPL=4×2+2×2+3×2+3×2=24。
二、哈夫曼树的定义
- 哈夫曼树是一种特殊的二叉树(其中哈夫曼二叉树是哈夫曼n叉树的一种,以下都以哈夫曼二叉树为例),树中所有叶子结点都带有权值,
带权路径长度最小的二叉树称为哈夫曼树,也称为最优二叉树。
哈夫曼树既不是满二叉树,也不是完全二叉树,只是一棵二叉树。
三、哈夫曼树的构造
哈夫曼树的构造步骤如下:
例如,给定一组权值为2,3,6,7,构造哈夫曼树并求其带权路径长度。
1、首先选取两棵根结点权值最小的树作为左、右子树,新的二叉树的根结点权值为其权值之和,然后将原先两个结点从森林中删除,新的结点添加进去。
2+3=5,相加后将这两个删除后,将5添加,如下图:
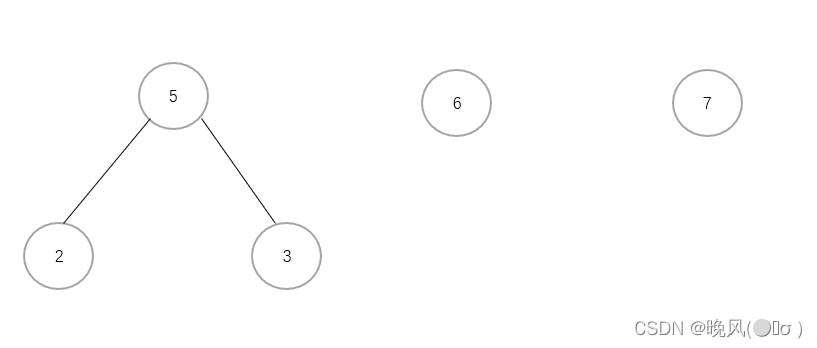
2、重复步骤1,继续选择两个权值最小的结点进行构造,然后将其从森林中删除,并将新的结点添加。
5+6=11,相加后将这两个删除后,将11添加,如下图:
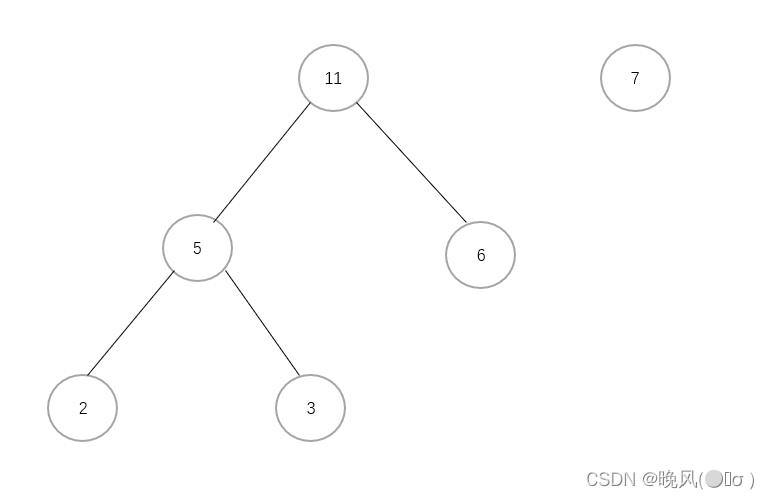
这样,就完成了由四个带权叶子结点构造成的哈夫曼树,如下:
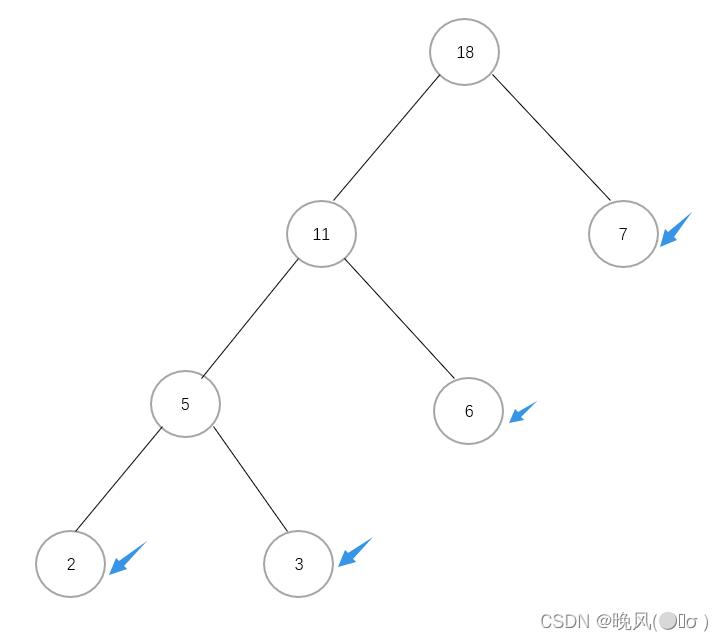
其带权路径长度为:WPL=2×3+3×3+6×3+7×3=54。
所以可以得到在由这四个结点为叶子结点的所有二叉树中,哈夫曼树的WPL是最短的。
三、固定/可变长度编码
哈夫曼编码是一种可变长度编码,以下将介绍固定/可变长度编码。
(一)固定长度编码
若对每个字符使用相同长度的二进制信息进行编码,则这种编码称为固定长度编码,简称为定长编码。
(二)可变长度编码(哈夫曼编码)
与固定长度编码相反,可变长度编码使用不等长的二进制信息进行编码,可变长度编码可以使字符的平均编码长度缩短,从而更好地压缩数据进行传输。
哈夫曼编码就是一种可变长度编码,它根据字符出现的概率来构造编码。
简单的来说,在哈夫曼编码中,字符的编码为根结点到该字符的路径上的边所标记的序列,规定左分支代表“0”,右分支代表“1”,从根结点到每个叶子结点所经过的路径分支所组成的0与1序列即为该结点对应字符的编码,如下对该哈夫曼树进行编码:
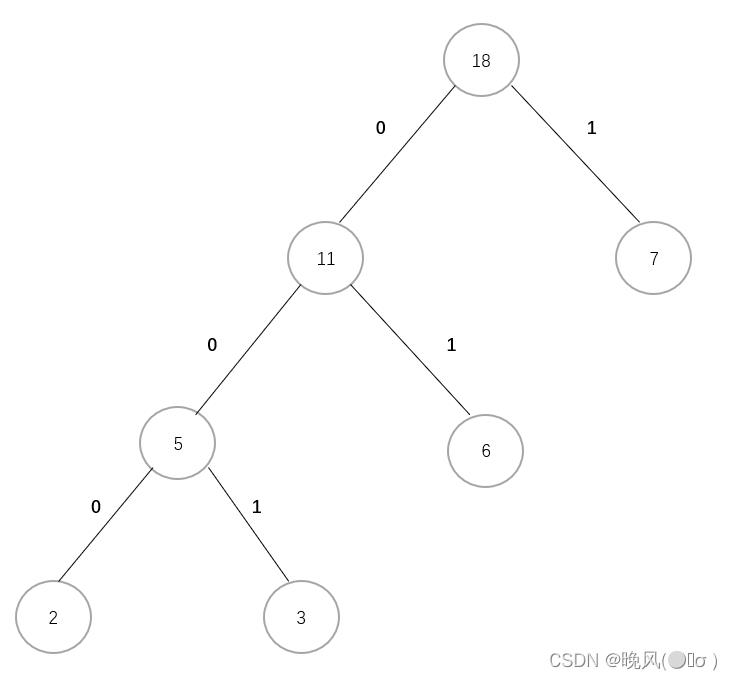
可以得到叶子结点的哈夫曼编码为:
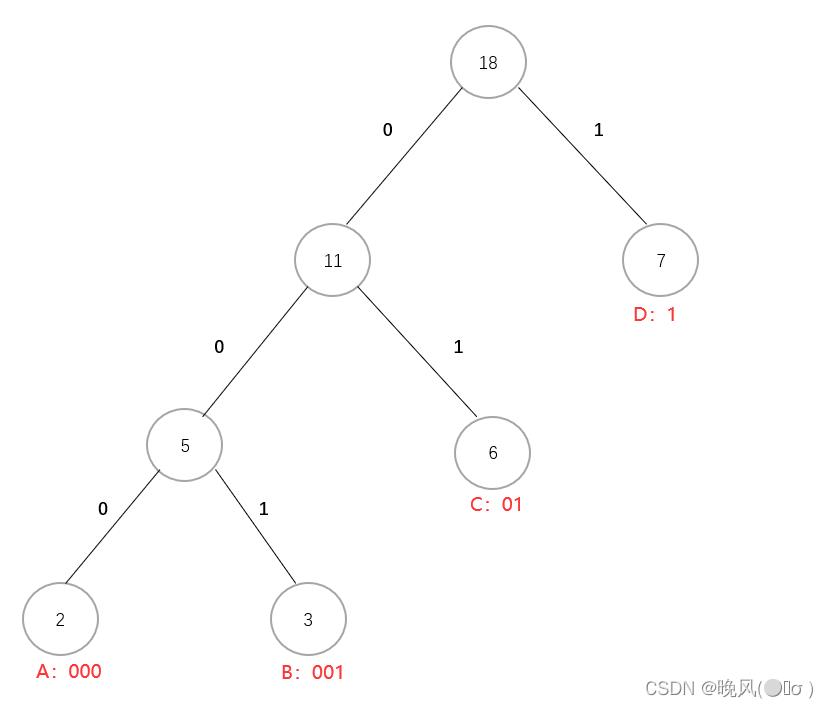
以上是关于数据结构学习笔记——哈夫曼树的主要内容,如果未能解决你的问题,请参考以下文章