矩形拼接 蓝桥杯 2154

Posted 2023-04-03 小梁今天敲代码了吗

问题描述

已知 3 个矩形的大小依次是 a1​×b1​,a2​×b2​ a3​×b3​ 。用这 3 个矩形能拼 出的所有多边形中, 边数最少可以是多少?

例如用 3×23×2 的矩形（用 A 表示)、 4×14×1 的矩形 (用 B 表示) 和 2×42×4 的矩 形（用 C 表示）可以拼出如下 4 边形。

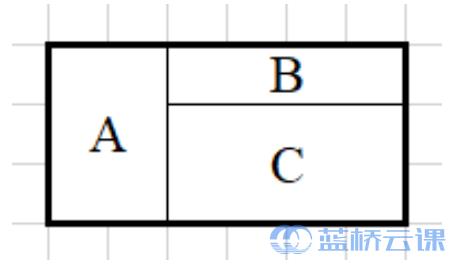
例如用3×2 的矩形 (用 A 表示)、 3×1 的矩形（用 B 表示) 和 1×1的矩 形（用 C 表示）可以拼出如下 6 边形。

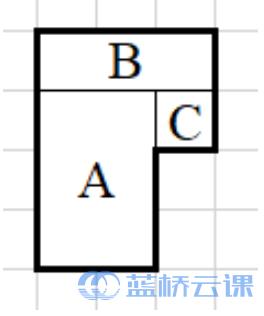
输入格式

输入包含多组数据。

第一行包含一个整数 T, 代表数据组数。

以下 T 行, 每行包含 6 个整数 a1​,b1​,a2​,b2​,a3​,b3​, 其中a1​,b1​ 是第一个矩 形的边长, a2​,b2​ 是第二个矩形的边长, a3​,b3​ 是第三个矩形的边长。

输出格式

对于每组数据, 输出一个整数代表答案。

样例输入

2
2 3 4 1 2 4
1 2 3 4 5 6

样例输出

4
6

思路：首先得分析三个矩阵拼在一起会有几种情况

四边形时

 1.当三个矩阵的边长有一边都相等时

2.像例子中那样，有两个矩阵的一个边相等，另外两个边之和跟第三个矩阵的一个边相等

六边形时

1.当两个矩阵的边长之和等于第三个矩阵的一条边

2.只有两个矩阵有一边相等

八边形时

其他情况均为八边形

def bian4(x1,x2,x3,a):
  if x1==x2+x3 and a[2]+a[3]-x2==a[4]+a[5]-x3:#如果有一边等于另外两个矩形一边之和，并且那两个矩形的另一条边长相等时的三种情况
    return True
  if x2==x1+x3 and a[0]+a[1]-x1==a[4]+a[5]-x3:
    return True
  if x3==x2+x1 and a[0]+a[1]-x1==a[2]+a[3]-x2:
    return True
  return False

def bian6(x1,x2,x3):#三个矩阵中的两个有一条边长相等时
    if x1==x2+x3 or x2==x1+x3 or x3==x2+x1:
        return True
    return False
    #3个矩阵拼接一共有3种情况，情况最好拼接完成有4条边，情况最差拼接出来有8条边，中间情况为6条边
N=int(input())
for n in range(N):
  edge = 8  # 最多是8条边
  a=list(map(int,input().split()))
  for i in range(0,2):#取第一个矩阵的边
    for j in range(2,4):#取第二个矩阵的边
      for k in range(4,6):#取第三个矩阵的边
        x1,x2,x3=a[i],a[j],a[k]#取出后的边进行分别判断情况
        if x1==x2 and x2==x3:#第一种情况，比较完美也就是三个矩阵都有一条边相等，这种情况就是4条边
          edge=min(edge,4)
        if bian4(x1,x2,x3,a):
                        #第二种情况，当有一个矩阵的边等于另外两个矩阵边的合，比如x1=x2+x3，这样就把第二个矩阵的x2边和第三个矩阵的x3边拼接在第一个矩阵x1上
                        #如果第二个矩阵除去x2这条边可以和第三个矩阵除去x3这条边可以重合也就是题给的第一个例子那么就是4条边
          edge=min(edge,4)
        if x1==x2 or x2==x3 or x1==x3:#第三种情况如果有两个矩阵有一条边相等，那么合并后就是6条边
          edge=min(edge,6)
        if bian6(x1,x2,x3):
                        #第四种情况，有一个矩阵的边等于另外两个矩阵边的合，比如x1=x2+x3但是仅仅满足这个条件
                        #也就是题目给的第二种情况，这样的情况就是6条边
          edge=min(edge,6)
  print(edge)

蓝桥杯_基础练习《矩形面积交---26》

/*  
基础练习 矩形面积交  
  
问题描述  
　　平面上有两个矩形，它们的边平行于直角坐标系的X轴或Y轴。对于每个矩形，我们  
  
给出它的一对相对顶点的坐标，请你编程算出两个矩形的交的面积。  
输入格式  
　　输入仅包含两行，每行描述一个矩形。  
　　在每行中，给出矩形的一对相对顶点的坐标，每个点的坐标都用两个绝对值不超过  
  
10^7的实数表示。  
输出格式  
　　输出仅包含一个实数，为交的面积，保留到小数后两位。  
样例输入  
1 1 3 3  
2 2 4 4  
样例输出  
1.00  
*/  
//矩形的相交面积。
#include<stdio.h>
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)<(y)?(x):(y))
int main(){
    double x1,y1,x2,y2;    //矩形1
    double x3,y3,x4,y4;    //矩形2
    double m1,n1;        //交集左上角坐标.
    double m2,n2;        //交集右下角坐标.
    scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
    scanf("%lf%lf%lf%lf",&x3,&y3,&x4,&y4);
    m1 = max(min(x1,x2),min(x3,x4));
    n1 = max(min(y1,y2),min(y3,y4));
    m2 = min(max(x1,x2),max(x3,x4));
    n2 = min(max(y1,y2),max(y3,y4));
    if(m2>m1 && n2>n1)
        printf("%.2f\\n",(m2 - m1)*(n2 - n1));
    else
        printf("0.00\\n");
    return 0;
}