八皇后问题(Python)
Posted Vaeeeeeee
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了八皇后问题(Python)相关的知识,希望对你有一定的参考价值。
一.问题简介
八皇后问题: 如何能在 8*8 的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了到达此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。
二.几种思路和方法
1.回溯法+递归思想
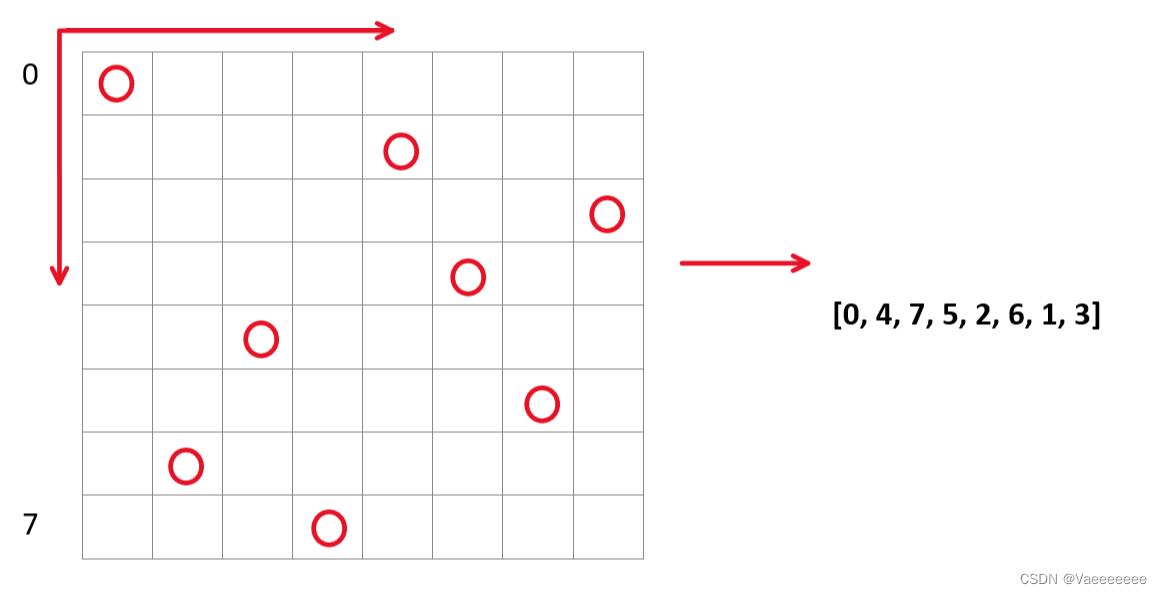
如图所示,圆圈代表皇后所放的位置,这里如果将棋盘转化为二维矩阵进行遍历比较麻烦,考虑到棋盘的每一行不能同时存在一个以上的皇后,所以将棋盘转化为一个具有八个元素的列表,而皇后的位置(i,j)对应的是列表中(元素的索引值,元素的值),因此放置皇后的操作变成了在列表中的每个位置填值操作,很明显的一个条件是列表中不能有相同的值。图中给出的是某一种情形
接下来直接看代码:
首先是定义一个queen函数,作用就是用来放皇后的位置。然后进入到第一个判断条件:如果当前行的位置遍历到“第9行”,即全部遍历完之后,将所有的结果放入到列表list中;然后是进入循环,在每一行的八个列的位置遍历,如果满足check中所有条件,那么直接递归调用,进入下一行遍历。
check函数:【任两个皇后都不能处于同一条横行】这一条件已经在前面保证成立了,这里只需保证剩下的两个条件【同一条纵行】和【同一条斜线】成立即可。注意:当两个皇后的位置坐标的连线斜率的绝对值为1,则这两个皇后在同一直线上。
def check(self, list, row):
for i in range(row):
if list[i] == list[row] or abs(list[row] - list[i]) == abs(row - i):
return False
return True
def queen(self, list, row, n): # list为存储的结果;row是当前行;n为棋盘大小
x=[]
if row == n:
x.extend(list)
self.solves.append(x)
return
for i in range(n): # 这里的i指的是所在列的值
list[row] = i
if self.check(list, row):
self.queen(list, row + 1, n)下面是完整代码:
导包:
import numpy as np # 提供维度数组与矩阵运算
import copy # 从copy模块导入深度拷贝方法
from board import Chessboard
棋盘类的初始化
# 初始化8*8八皇后棋盘
chessboard = Chessboard()
# 基于棋盘类,设计搜索策略
class Game:
def __init__(self, show = True):
"""
初始化游戏状态.
"""
self.chessBoard = Chessboard(show)
self.solves = []
self.gameInit()
# 重置游戏
def gameInit(self, show = True):
"""
重置棋盘.
"""
self.Queen_setRow = [-1] * 8
self.chessBoard.boardInit(False)
def check(self, list, row):
for i in range(row):
if list[i] == list[row] or abs(list[row] - list[i]) == abs(row - i):
return False
return True
def queen(self, list, row, n): # list为存储的结果;row是当前行;n为棋盘大小
x=[]
if row == n:
x.extend(list)
self.solves.append(x)
return
for i in range(n): # 这里的i指的是所在列的值
list[row] = i
if self.check(list, row):
self.queen(list, row + 1, n)
def run(self, row=0):
#self.solves.append([0, 6, 4, 7, 1, 3, 5, 2])
n = 8
list = [0 for _ in range(n)]
self.queen(list,row,n)
def showResults(self, result):
"""
结果展示.
"""
self.chessBoard.boardInit(False)
for i,item in enumerate(result):
if item >= 0:
self.chessBoard.setQueen(i,item,False)
self.chessBoard.printChessboard(False)
def get_results(self):
"""
输出结果.
return: 八皇后的序列解的list.
"""
self.run()
return self.solves
验证一下结果:
game = Game()
solutions = game.get_results()
print('There are results.'.format(len(solutions)))
game.showResults(solutions[0])
可以直接输出所有的结果(92种):
print(solutions)2.排列组合的思想
在上面的基础上,可以稍微转化一下思路,放置不同的皇后位置就是将不同的八个元素的作排列组合问题,然后只要再保证“不在同一斜线”这个条件就可以了。下面是代码:
list1=[0,1,2,3,4,5,6,7]
result=[]
final_result=[]
from itertools import permutations #permutations函数:可以对集合或字符串进行排序或排列的所有可能的组合
for i in permutations(list1,8):
result.append(i) #转化为排列组合问题,result存储部分可能的结果
#下面只需要从result中找出满足‘任一两个皇后不在同一斜线上’的结果
for i in result:
n=0 #n用以标记那些满足条件的结果;
for j in enumerate(i):
for m in enumerate(i):
if m!=j and abs(m[0]-j[0])==abs(m[1]-j[1]): #m!=j是避免对同一个坐标位置进行判断
n+=1 #只要有两个坐标的连线斜率为1,n就不为0
if n==0:
final_result.append(i)
print(len(final_result))
print(final_result)
3.遗传算法
基本原理和步骤
遗传算法将要解决的问题模拟成一个生物进化的过程,通过复制、交叉、突变等操作产生下一代的解,并逐步淘汰掉适应度函数值低的解,增加适应度函数值高的解。这样进化N代后就很有可能会进化出适应度函数值很高的个体。
其计算步骤如下:
(1) 编码:将问题空间转换为遗传空间;
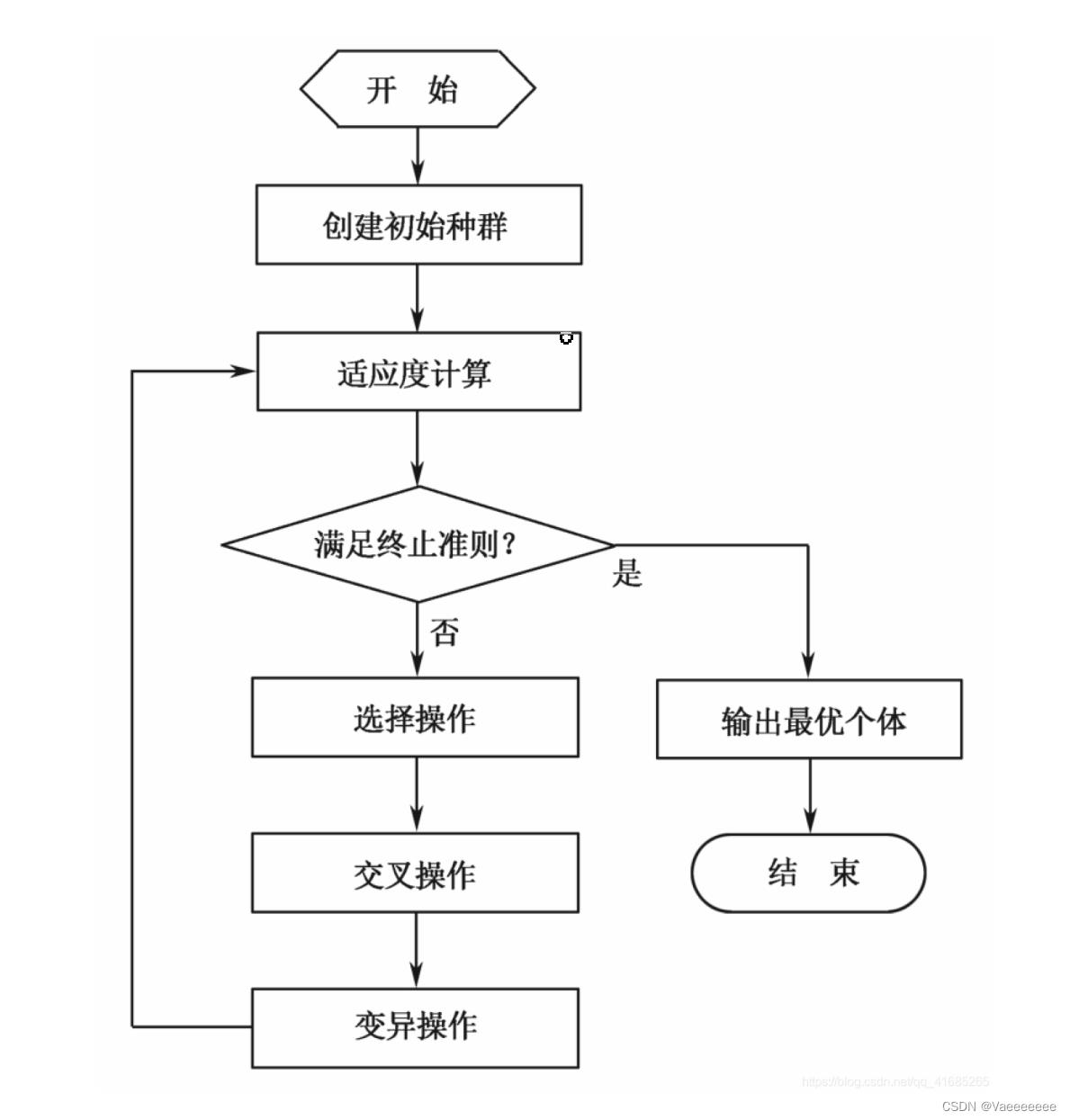
(2)创建初始种群:随机生成P 个染色体作为初始种群;
(3)适应度计算:染色体评价,计算各个染色体的适应度;
(4)选择操作:根据染色体适应度,按选择算子进行染色体的选择;
(5)交叉操作:按交叉概率进行交叉操作;
(6)变异操作:按变异概率进行变异操作;
(7)返回(4)形成新的种群,继续迭代,直到满足终止条件。
具体实现代码部分还在写,以后有机会在续上吧。
觉得不错的话,大家给个关注给个赞吧!
八皇后问题遗传算法实现(python版)
八皇后问题的遗传算法实现过程详解
1、八皇后问题描述
19 世纪著名的数学家Gauss 在1850 年提出八皇后问题后, 该问题成为各类语言程序设计的经典题目。八皇后问题要求在8×8 格的国际象棋上摆放八个皇后,使横、竖、斜方向上都不能有两个及两个以上皇后在同一条直线上, 问题也可以推广到N 个皇后。穷举法在问题规模不大的情况下还可适用,回溯法是求解此问题的经典算法。但N 皇后问题是个NP 难问题, 随着皇后数目的增多, 求解复杂度激增, 就需利用非常规的技术求解。遗传算法在求解一些NP 完全问题上得到了广泛地应用,本文用遗传算法求解八皇后问题,给出详细的实现过程。
2、基本遗传算法求解过程
基本遗传以初始种群为基点, 经过选择、交叉、变异操作生成新的种群,如此更新种群直到满足终止条件。其计算步骤如下:
(1) 将问题空间转换为遗传空间, 也就是编码;
(2)随机生成P 个染色体作为初始种群;
(3)染色体评价,也就是按确定的适应度函数
计算各个染色体的适应度;
(4)根据染色体适应度,按选择算子进行染色体的选择;
(5)按交叉概率进行交叉操作;
(6)按变异概率进行变异操作;
(7)返回(4)形成新的种群,继续迭代,直到满足终止条件。
基本遗传算法给出了基本框架, 针对求解的问题不同, 遗传算法在相应的计算步骤中有不同的设计。本文针对八皇后问题, 设计了相应的编码,适应度计算方法,交叉和变异操作。
3、用遗传算法求解八皇后问题实现过程详解
3.1 编码
遗传算法中传统的编码是二进制编码, 本文采用多值编码。染色体长度取决于皇后的个数。染色体中每个基因所处的位置表示其在棋谱中所在的行数, 基因值表示其所在的列数。如染色体40752613 表示:从0 开始数,第0 个4 表示在第零行的皇后在第4 列, 第1 个0 表示第一行的皇后在第0 列,以此类推。八皇后问题中皇后不能处于同行同列, 意味着染色体中0~7 的基因取值不能出现重复。
3.2 个体评价
染色体通常表示了问题的可行解, 对可行解进行遗传操作寻找最优解。但在八皇后问题中,染色体仅仅体现同行同列中未出现互攻, 在对角线上是否出现互攻还未做考虑。在对皇后的位置做比较的时候, 可以对两个棋子的行数差与列数差进行对比, 实现了互攻次数的统计。公式为:|绝对值((y2-y1)/(x2-x1)) |=1。公式中(x1,y1),(x2,y2)分别表示两个皇后所在的位置,即所在的行数和列数。当两个皇后的行数差与列数差比值的绝对值为1 的时候,两皇后在同一对角线上,即出现了互攻。每个染色体内的互攻次数为Value,初始值设为0;第0 行与1~7 行进行比较, 每出现一次互攻则Value 的值增加1;第1 行与2~7 行进行比较,以此类推来计算Value 值。当Value 为0 表示没有发生互攻,此染色体就是其中的一个可行解。当Value 不为0则进行适应度的计算。一般来说, 适应度越大越
好,而互攻次数为越小越好,所以可以将适应度的计算函数设置为:F=28-Value。
3.3 选择
选择使用的是经典的赌轮选择方法, 与基本遗传算法的实现无特别之处,此处不赘述。
3.4 交叉
经典的单点, 多点等交叉因染色体中不能出现重复的基因值,在该问题中不适用。本文使用部分匹配交叉,具体操作如下:
1)在染色体中随机选取两个点标记为y,
如:染色体a:01y24y3675;
染色体b:12y30y4576;
两个y 之间的基因段称为中间段, 记录其对应关系2-3,4-0;
2)对染色体a,b 的中间段进行交换,
形成染色体a\':01y30y3675;染色体b\': 12y24y4576;
3) 利用对应关系,对染色体a\', b\' 中间段外的基因进行交换,
形成 染色体a\'\': 41y30y2675;
染色体b\'\': 13y24y0576;
交叉完成。
3.5 变异
采用多值编码后, 变异操作并不能通过简单的0,1 反转实现。
本文采取随机地选取染色体内的两个基因进行交换来实现。
例如随机选取的是
6 和1 两个基因,那么
变异前染色体: 7 (6) 5 4 3 2 (1) 0
变异后染色体: 7 (1) 5 4 3 2 (6) 0
3.6 终止策略
本文采用的终止策略为: 当群体中出现染色体的适应值为0 时, 即表示算法搜索到了一个可行解,终止算法。若算法运行设置的代数还未找到可行解,同样终止程序运行。
4、总结
本文详细介绍了用遗传算法求解八皇后问题的求解过程, 但要注意的是这只是其中的一种编码,交叉,变异等操作设计方法,还有许多其他的方法可以选择。对于各操作采取不同设计方案的遗传算法,其算法性能值得比较讨论。
1 # 2 # 遗传算法(八皇后问题) 3 # 最佳值28 4 import random 5 import numpy 6 7 8 N=8 #皇后数 9 Cluster_size=12 #默认种群大小 10 LASTG=100 #/*终止后代*/ 11 MRATE=0.8 #/*突变的概率*/ 12 array=numpy.zeros((Cluster_size,N)).astype(int) #染色体集合 13 narray=numpy.zeros((Cluster_size * 2,N)).astype(int) #下一代染色体集合 14 _array=numpy.zeros((Cluster_size,N)).astype(int)#array数组的副本 15 values=numpy.zeros(Cluster_size).astype(int) #评估数组 16 max_array=numpy.zeros(N).astype(int) #保存最佳数组 17 generation = 0 #记录代数 18 signal = -1 # 信号 19 max = -1 # 记录当前最优值 20 max_generation = -1 #记录当前最优值代数 21 22 23 24 class Struct: 25 key = numpy.zeros(N).astype(int) 26 values = numpy.zeros(N).astype(int) 27 28 29 rember=Struct() 30 31 32 def rndn(l): 33 rndno =random.randint(0,l-1) 34 return rndno 35 36 37 def copy_array(): 38 for i in range(Cluster_size): 39 for j in range(N): 40 _array[i][j]=array[i][j] 41 42 43 def output_copy_array(): 44 for i in range(Cluster_size): 45 for j in range(N): 46 print(_array[i][j],end=" ") 47 print() 48 49 50 def the_answer(values,size): 51 for i in range(size): 52 if values[i]==28: 53 return i 54 return -1 55 56 57 def judge(a,n): 58 value = -1 59 for i in range(n): 60 value = a[i] 61 j=i+1 62 while j<n: 63 if(value==a[j]): 64 return 0 65 j+=1 66 return 1 67 68 69 70 def count_collidecount(): 71 value=0 72 global signal 73 for i in range(Cluster_size): 74 for j in range(N): 75 x1=j 76 y1=array[i][j] 77 m=j+1 78 while m<N: 79 x2=m 80 y2=array[i][m] 81 if (abs((y2-y1)/(x2-x1))==1): 82 value+=1 83 m+=1 84 values[i]=28-value 85 value=0 86 signal= the_answer(values,Cluster_size) 87 88 89 90 def count_generation_collidecount(values,cluster_size): 91 value=0 92 for i in range(cluster_size): 93 for j in range(N): 94 x1=j 95 y1=narray[i][j] 96 m=j+1 97 while m<N: 98 x2=m 99 y2=narray[i][m] 100 if(abs((y2 - y1) / (x2 - x1))==1): 101 value+=1 102 m+=1 103 values[i]=28-value 104 value=0 105 106 107 # /************************/ 108 # /* selectp()函数 */ 109 # /* 父代的选择 */ 110 # /************************/ 111 def selectp(roulette,totalfitness): 112 acc=0 113 ball=rndn(totalfitness) 114 for i in range(Cluster_size): 115 acc+=roulette[i] 116 if (acc>ball): 117 break 118 return i 119 120 121 def takeoutrepeat( position): 122 signal=True 123 for i in range(N): 124 value = narray[position*2][i] 125 j=i+1 126 while j<N: 127 if (narray[position*2][j]==value): 128 # print("there have reapt number: "+str(position*2)) 129 signal=False 130 j+=1 131 for i in range(N): 132 value=narray[position*2+1][i] 133 j=i+1 134 while j<N: 135 if (narray[position*2+1][j]==value): 136 # print("there have reapt number: "+str(position*2+1)) 137 signal=False 138 j+=1 139 return signal 140 141 142 143 144 def judge_reapt(c, cluster): 145 value =0 146 arraysEqual =True 147 i=0 148 for j in range(cluster): 149 while (arraysEqual and i<N): 150 if (narray[c][i] !=_array[j][i]): 151 arraysEqual=False 152 i+=1 153 if(arraysEqual): 154 value+=1 155 else: 156 arraysEqual=True 157 i=0 158 159 if(value>0): 160 return False 161 else: 162 return True 163 164 165 166 167 # /************************/ 168 # /* selection()函数 */ 169 # /* 选择下一代 */ 170 # /************************ 171 172 def selection(): 173 global signal 174 global max_generation 175 global max 176 totalfitness=0 177 roulette=numpy.zeros(Cluster_size*2).astype(int) 178 acc=0 179 for i in range(Cluster_size): 180 totalfitness=0 181 count_generation_collidecount(roulette,Cluster_size*2) 182 c=0 183 while c<Cluster_size*2: 184 totalfitness+=roulette[c] 185 c+=1 186 signal=the_answer(roulette,Cluster_size*2) 187 188 while True: 189 ball =rndn(totalfitness) 190 acc=0 191 c=0 192 while c<Cluster_size*2: 193 acc+=roulette[c] 194 if acc>ball: 195 break 196 c+=1 197 judge=judge_reapt(c,Cluster_size) 198 if judge==True: 199 break 200 #/ *染色体的复制 * / 201 for j in range(N): 202 array[i][j]=narray[c][j] 203 204 for q in range(Cluster_size*2): 205 if roulette[q]>max: 206 max =roulette[q] 207 max_generation = generation 208 for i in range(N): 209 max_array[i]=narray[q][i] 210 print(roulette[q], end=" ") 211 print() 212 213 214 215 216 217 218 def judgein(m,location1,location2): 219 i=location1 220 while i<=location2: 221 if ((m == rember.key[i]) | (m == rember.values[i])): 222 return i 223 i+=1 224 return -1 225 226 227 228 229 230 231 # /************************/ 232 # /* crossing()函数 */ 233 # /* 特定2染色体的交叉 */ 234 # /************************/ 235 def crossing(mama, papa,position): 236 while True: 237 while True: 238 cp1 = rndn(N) 239 cp2 = rndn(N) 240 if cp1 != cp2: 241 break 242 # print("cp1="+str(cp1)+"cp2="+str(cp2)) 243 if cp1<cp2: 244 location1 = cp1 245 location2 = cp2 246 else: 247 location1 = cp2 248 location2 = cp1 249 250 i = location1 251 while i<=location2: 252 rember.key[i] = array[mama][i] 253 rember.values[i] = array[papa][i] 254 # 交换中间段 255 narray[position*2][i] = array[papa][i] 256 narray[position*2+1][i] = array[mama][i] 257 i+=1 258 # 利用对应关系,对染色体mama和papa, 中间段外的基因进行交换 259 #/ * 交换前半部分 * / 260 for j in range(location1): 261 weizhi = judgein(array[mama][j],location1,location2) 262 # print("weizhi= "+str(weizhi)) 263 if (weizhi == -1): 264 narray[position*2][j] = array[mama][j] 265 else: 266 if (array[mama][j] == rember.key[weizhi]): 267 narray[position*2][j] = rember.values[weizhi] 268 else: 269 narray[position*2][j] = rember.key[weizhi] 270 weizhi = judgein(array[papa][j], location1, location2) 271 if (weizhi == -1): 272 narray[position*2+1][j] = array[papa][j] 273 else: 274 if (array[papa][j] == rember.key[weizhi]): 275 narray[position*2+1][j] = rember.values[weizhi] 276 else: 277 narray[position*2+1][j] = rember.key[weizhi] 278 279 280 #/ *交换后半部分 * / 281 j = location2+1 282 while j<N: 283 weizhi = judgein(array[mama][j], location1, location2) 284 if (weizhi == -1): 285 narray[position*2][j] = array[mama][j] 286 else: 287 if (array[mama][j] == rember.key[weizhi]): 288 narray[position*2][j] = rember.values[weizhi] 289 else: 290 narray[position*2][j] = rember.key[weizhi] 291 weizhi = judgein(array[papa][j],location1,location2) 292 if (weizhi == -1): 293 narray[position*2+1][j] = array[papa][j] 294 else: 295 if (array[papa][j] == rember.key[weizhi]): 296 narray[position*2+1][j] = rember.values[weizhi] 297 else: 298 narray[position*2+1][j] = rember.key[weizhi] 299 j+=1 300 301 signal = takeoutrepeat(position) 302 # print("--------------signal= "+str(signal)) 303 if (signal != False): 304 break 305 306 307 308 309 310 311 # /************************/ 312 # /* notval()函数 */ 313 # /* */ 314 # /************************/ 315 def notval(i): 316 while True: 317 position1 =rndn(N) 318 position2 =rndn(N) 319 if position1 != position2: 320 break 321 temp=narray[i][position2] 322 narray[i][position2] = narray[i][position1] 323 narray[i][position1] =temp 324 325 326 327 328 # /***********************/ 329 # /* mutation()函数 */ 330 # /* 突变 */ 331 # /***********************/ 332 def mutation(): 333 for i in range(Cluster_size*2): 334 if (rndn(100) / 100 <= MRATE): 335 #/ *染色体突变 * / 336 notval(i) 337 print("mutation is complete") 338 339 340 341 342 343 def mating(): 344 totalfitness =0 345 roulette=numpy.zeros(Cluster_size).astype(int) 346 print(len(roulette)) 347 # 生成轮盘 348 for i in range(Cluster_size): 349 roulette[i] = values[i] 350 totalfitness += roulette[i] 351 # 选择和交叉的循环 352 for i in range(Cluster_size): 353 while True: 354 mama=selectp(roulette,totalfitness) 355 papa=selectp(roulette,totalfitness) 356 if mama != papa: 357 break 358 # 特定2染色体的交叉 359 crossing(mama,papa,i) 360 361 362 363 def outputrember(): 364 for i in range(N): 365 print("key= "+rember.key[i]+"values= "+rember.values[i]) 366 367 368 369 370 def outputnarray(): 371 for i in range(Cluster_size*2): 372 if (i % 2 ==0): 373 print("------------------------------") 374 for j in range(N): 375 print(narray[i][j],end=" ") 376 print() 377 378 379 380 381 def output(): 382 global max 383 global max_generation 384 for i in range(Cluster_size): 385 if values[i]>max: 386 max =values[i] 387 max_generation=max_generation 388 print(values[i],end=" ") 389 print() 390 391 392 393 394 def outputarray(): 395 for i in range(Cluster_size): 396 for j in range(8): 397 print(array[i][j], end =" ") 398 print() 399 400 401 402 403 404 def init_Cluster(): 405 print(\'fsadsgagasgs\') 406 a=[0 for n in range(8)] 407 count=0 408 while count < Cluster_size: 409 for y in range(8): 410 x= random.randint(0,7) #产生0到7的随机数 411 a[y]=x 412 if(judge(a,8)): 413 for i in range(8): 414 array[count][i]=a[i] 415 else: 416 count=count-1 417 count+=1 418 419 420 421 422 423 def main(): 424 global generation 425 init_Cluster() 426 while generation<LASTG: 427