基于Lambert函数的时滞系统稳定性研究

Posted 2022-08-03 studyer_domi

1、内容简介

略
426-可以交流、咨询、答疑

2、内容说明

随着当今世界网络技术、通信技术和计算机技术的快速发展以及在各个领域的广泛应用。尤其是在电力系统的研究上，随着技术不断的发展和革新，逐步应用到电力生产和电力供应系统中，提供了稳定的电力传输途径，朝着智能化的方向前行。这些技术也使得电力系统的监测、分析和控制方式向着广域化、网络化和智能化方向发展，而在电力系统中有着一个重要的特性即为时滞特性，我们所要研究的就是在电力系统中Lambert函数下时滞系统稳定性。就目前来说，国内外学者在分析电力系统时，忽略了时滞特性的影响。但是电力系统的构成是很复杂、庞大的，当大功率需要远距离的传输时，传输线路上会发生功率振荡的可能性和危害性就会变大，仅靠局部所设计的控制器是难以保证电力系统的稳定性。而且电力系统往往是一个非线性、具有随机性的时滞动力系统，时滞的存在是系统不稳定的根源，即使是较小的时滞也会造成控制器失效，甚至是造成灾难性事故，因此，在许多情况下，必须将电力系统建模为时滞系统进行研究，运用好时滞系统的稳定性，以全系统的视角实施广域优化控制才能确保系统的安全稳定运行。

时滞系统是系统组成部分固有的时间延迟，或是因为控制目的而引入的时间延迟系统。时滞系统可以通过延迟微分方程来表示，是属于泛微分方程的一类，并且在过去的几十年里已经得到了大量的研究。从电力与自动化工程到生物、化学、物理系统和生态学，都会引用时间延迟。这样的时间延迟可以限制和降低控制系统的可实现的性能，甚至会引起系统不稳定性。在各种时滞系统中，对象的纯滞后时间对控制系统的控制性能有极大的危害，它不仅使得系统的稳定性降低，过渡过程的特性变坏，而且纯滞后占整个动态过程的时间越长，难控的程度越大，因此时滞系统的控制问题已经成为了困扰着自动控制领域的一大难题。对于时滞系统，最为重要的就是控制，对时滞特性的控制是很普遍。在时滞系统控制的发展历程中，出现了Smith预估控制、大林算法、自适应控制、预测控制、变结构控制及智能控制器等各种控制方法在时滞系统中的应用，综述了这些方法的优点与缺陷，总结出复合控制才是控制时滞系统有效而实用的方法，而且有着大好的应用前景。由此可见，时滞系统的重要性不言而喻，而我们正要研究的是如何解决时滞系统的稳定性问题，怎样达到好的控制效果。

Lambert W函数也叫做欧米加函数或乘数对数，它是一个多值函数，有无穷多个分支，而且每一个分支都是一个单值函数，在实数范围内有W(x0)和W（x1）两支，其中前者称为Lambert W函数的主支。Lambert W函数也是f(W)=Wexp(W)的反函数，exp(W)是指数函数，W是任意复数。一直以来，国内外学者对该函数也有了一定的研究。在最初，只是用它来解决一些基础数学问题，比如含有指数的方程，时滞微分方程，在组合数学中的树的计算等。而且，随着对该函数的深入研究，发现了它的更多用途，由数学延伸到了物理、化学、生物等领域中，如在量子化学，统计力学中一些问题都是用W函数来解决。尤其是一些复杂的问题，应用Lamberr W函数表示要方便很多，一些方程解可用它表示出来，再加上目前相关数学软件的发展如Matlab,Maple等，都提供相应的函数计算Lambert W函数，为这些方程解的高精度计算提供了可能，也为研究时滞系统的稳定性提供了便捷。

3、仿真分析

clc
close all
clear
%% 一阶
tao = 1;
Kp = -2;
k = -4:4;
alpha = 1;
for i = 1:length(k)
    x = -Kp*tao*exp(tao*alpha);
    y = lambertw(k(i),x);
    s(i) = y/tao-alpha;
end
figure
plot(real(s),imag(s),'marker','.','markersize',18,'color','black')
xlabel 实部
ylabel 虚部
set(gcf,'color','w');

%% 二阶
% -------------- Kp = -2 ------------------------------
n = 2;
Kp = -2;
alpha = 1;
tao = 1;
k = -4:4;

l = 0;
for i = 1:length(k)
    if Kp<0
        x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*2*l*pi/n);
        y = lambertw(k(i),x);
        s0(i) = n/tao*y-alpha;
    else
        x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*(2*l+1)*pi/n);
        y = lambertw(k(i),x);
        s0(i) = n/tao*y-alpha;
    end
end
l = 1;
for i = 1:length(k)
    if Kp<0
        x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*2*l*pi/n);
        y = lambertw(k(i),x);
        s1(i) = n/tao*y-alpha;
    else
        x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*(2*l+1)*pi/n);
        y = lambertw(k(i),x);
        s1(i) = n/tao*y-alpha;
    end
end

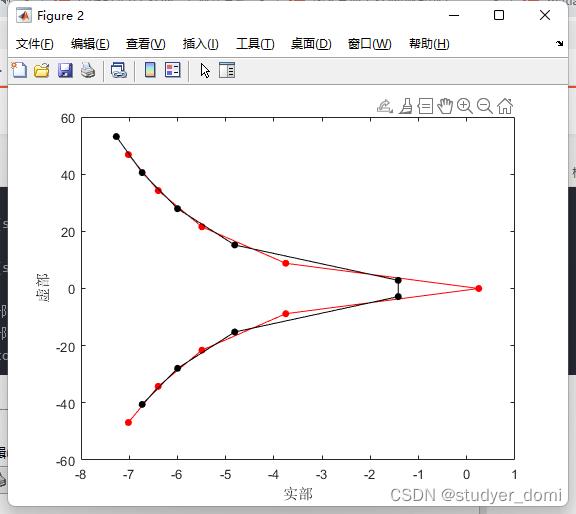
figure
plot(real(s0),imag(s0),'marker','.','markersize',18,'color','red')
hold on
plot(real(s1),imag(s1),'marker','.','markersize',18,'color','black')
hold off 
xlabel 实部
ylabel 虚部
set(gcf,'color','w');

% -------------- Kp = 2 ------------------------------
n = 2;
Kp = 2;
alpha = 1;
tao = 1;
k = -4:4;

l = 0;
for i = 1:length(k)
    if Kp<0
        x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*2*l*pi/n);
        y = lambertw(k(i),x);
        s0(i) = n/tao*y-alpha;
    else
        x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*(2*l+1)*pi/n);
        y = lambertw(k(i),x);
        s0(i) = n/tao*y-alpha;
    end
end
l = 1;
for i = 1:length(k)
    if Kp<0
        x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*2*l*pi/n);
        y = lambertw(k(i),x);
        s1(i) = n/tao*y-alpha;
    else
        x = tao/n*exp(tao/n*alpha)*abs(Kp)^(1/n)*exp(1i*(2*l+1)*pi/n);
        y = lambertw(k(i),x);
        s1(i) = n/tao*y-alpha;
    end
end

figure
plot(real(s0),imag(s0),'marker','.','markersize',18,'color','red')
hold on
plot(real(s1),imag(s1),'marker','.','markersize',18,'color','black')
hold off 
xlabel 实部
ylabel 虚部
set(gcf,'color','w');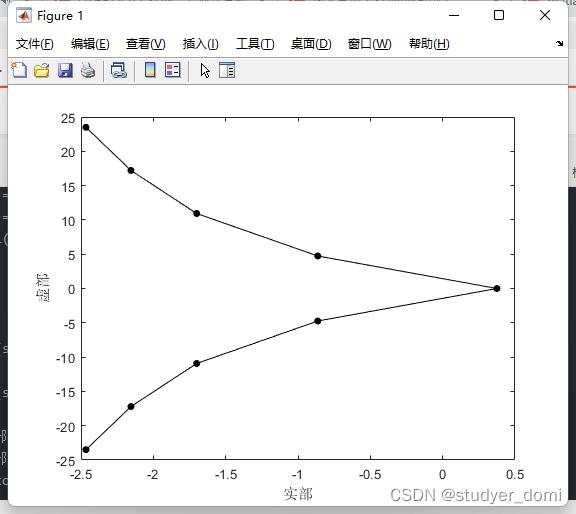

4、参考论文

A note on the use of the LambertW function in the stability analysis of time-delay systems 龙敏,周铁军. Lambert W函数性质及其应用[J]. 衡阳师范学院学报, 2011, 32(06): 38-40.