贪心算法：最小生成树Prim算法

Posted 2023-04-02 starry陆离

👨‍🎓作者简介：一位喜欢写作，计科专业大二菜鸟

🏡个人主页：starry陆离

🕒首发日期：2022年5月31日星期二

🌌上期文章：动态规划:多重背包问题

📚订阅专栏：算法分析与设计
如果文章有帮到你的话记得点赞👍+收藏💗支持一下哦

贪心算法：最小生成树Prim算法

• 笔者前言
• 1.问题引入
• 2.最小生成树
• 3.设计思路
• 4.图解算法
• 5.完整代码

---

笔者前言

这是大一暑假的c笔记，再一次写prim算法笔记又有一点点进步
最小生成树（Prim普利姆算法和Kruskal算法）

1.问题引入

若要将n个城市之间原有的公路改造为 高速公路，这些城市之间原有公路网 如图所示，每条边上的数字表示高 速公路的改造成本（单位：10亿元）。 如何以最低的成本来构建高速公路网， 使得任意两个城市之间都有高速公路 相连？

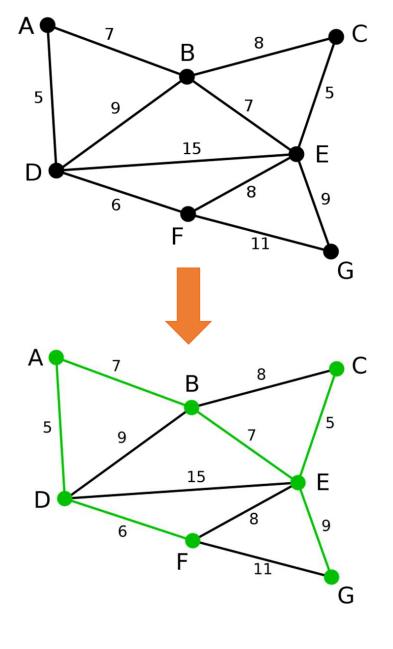
2.最小生成树

Minimal Spanning Trees (MST)

• 任何只由图G的边构成，并包含G的所有顶点的树称为G的生成树
• 加权无向图G的生成树的权重是该生成树的所有边的权重之和
• 最小生成树是其所有生成树中权重最小的生成树
• N个顶点，选取N-1条边，构建一个连通图，且这N-1条边的权重之和最小

3.设计思路

1. 任意选定一点s，设集合S=s （Prim算法的特点从点出发）

2. 从不在集合S的点中选出一个点j使得其与S内的某点i的距离最短，则(i，j) 就是生成树上的一条边，同时将j点加入S

3. 转到(2)继续进行，直至所有点都己加入S集合，所以一棵有n个顶点的图构成的最小生成树有n-1条边

因此我们设计这个算法时需要保存的信息有：

• 数组e[][]来记录图的各边权重
• 数组visited[j]来保存当前节点j是否被访问（是否在集合s中）
• 数组dis[j]记录不在集合S的点中的节点j与S内的某点i的距离最短距离
• 数组close[j]记录顶点j的最近邻接点

4.图解算法

首先我们要储存这张图，用一个二维数组e[][]即可，并且初始化时这个图上各点的距离应该为无穷大，表示各点没有连通

//初始化各边均不相邻
for(int i=0;i<n;++i) 
    for(int j=0;j<n;++j) 
        e[i][j]=Integer.MAX_VALUE;
    


//录入各边的信息
int x,y;
for(int i=0;i<m;++i) 
    x=scanner.nextInt();
    y=scanner.nextInt();
    e[x][y]=scanner.nextInt();
    e[y][x]=e[x][y];//可别忘了这一行哦，无向图的存储

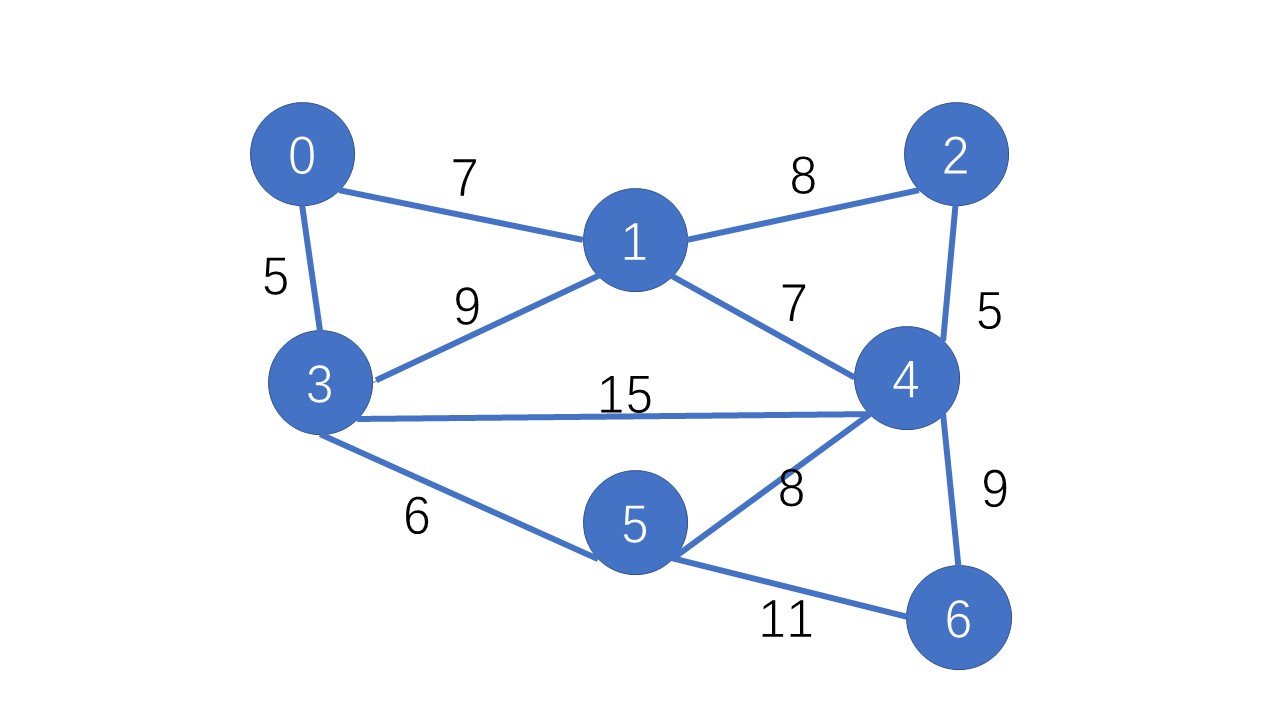
其次我们任选一点，一般都是从最小的顶点开始，如0点；将其加入集合S中，这时要做的操作就多着，首先要获取其他顶点到第1个点(0)的距离，不直接相邻的顶点距离为无穷大；其次初始化所有点的最近邻接点都为第1个点(0)；最后还要将第1个点加到S中，更新visited[0]=1;

//初始化，S中只有第1个点(0)
    for(int i=0;i<n;++i) 
        dis[i]=e[0][i];//获取其他顶点到第1个点(0)的距离，不直接相邻的顶点距离为无穷大
        close[i]=0;//初始情况下所有点的最近邻接点都为第1个点(0)
        visited[i]=0;//初始情况下所有点都没有被访问过
    

    visited[0]=1; //访问第1个点(0)，将第1个点加到S中

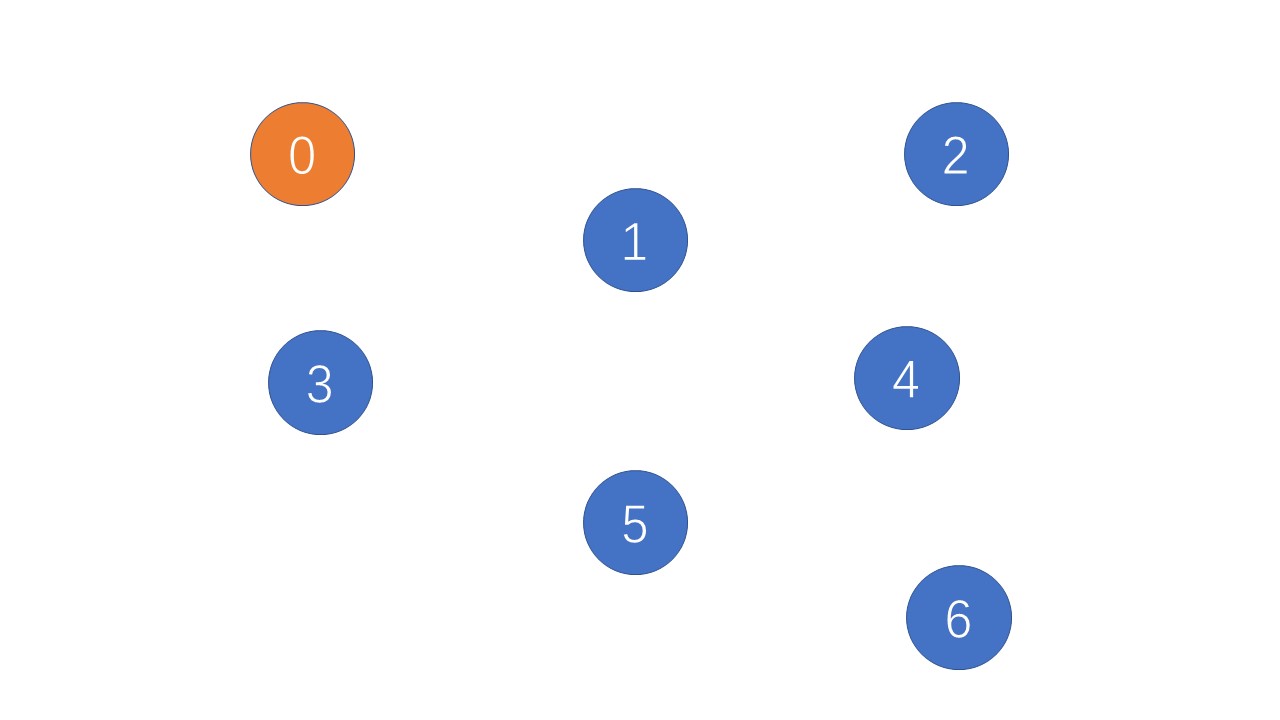
接下来要做的事就头大了。我们要遍历剩下的所有点，直到所有的点都加入到集合S中，慢慢来我们一个一个加。所要做的操作就是：

• 从不在集合S的点中选出一个点j使得其与S内的某点i的距离最短，则(i，j) 就是生成树上的一条边，同时将j点加入S

这时集合S中只有一个点（0），那么遍历找到不再集合S中的其他点到点（0）的最小的距离，我们发现是点（0）和点（3）最近，距离为5；用一个遍历index记录这个点，并更新visited[3]=1表示将点（3）加入到集合S中

int index=0;				
//如果顶点k没有被使用，且到S的距
//离小于k到S的距离，将k赋给index 
for(int k=0;k<n;++k) 
    if(visited[k]==0&&dis[k]<dis[index]) 
        index=k;//记录到S距离最小的顶点
    

//将顶点index加入集合S并更新dis[]数组
	visited[index]=1;

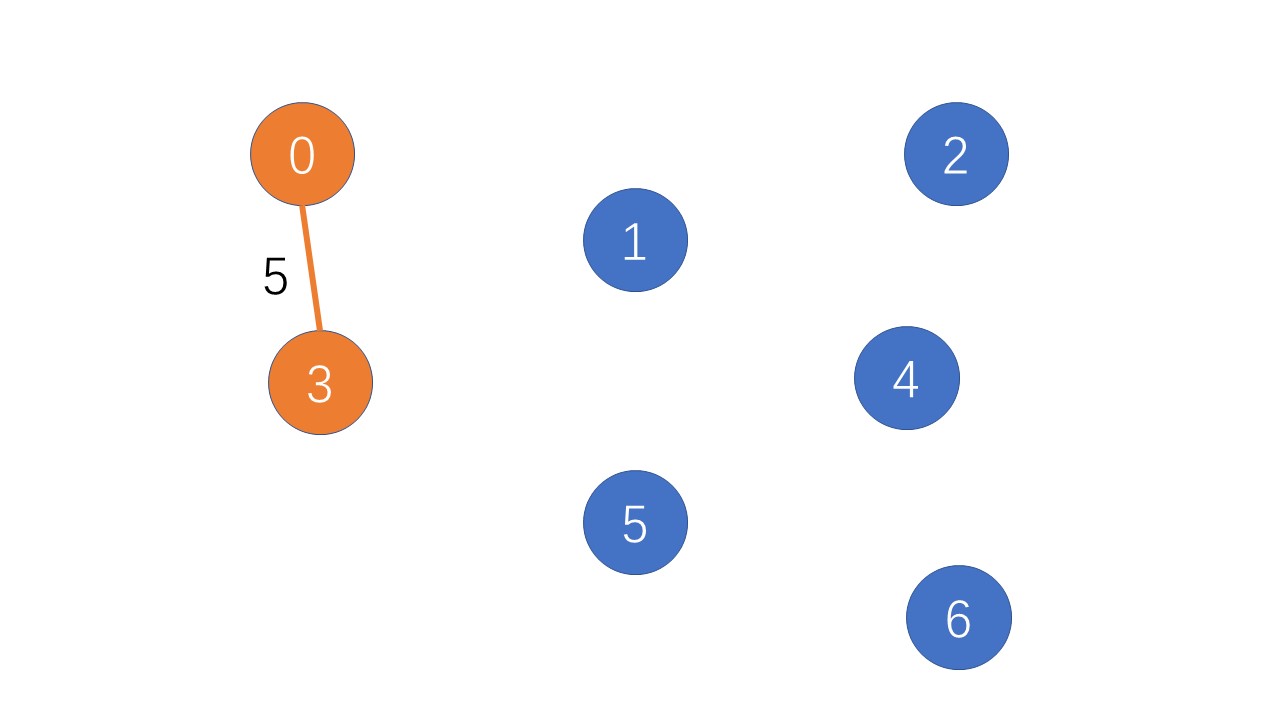
这可没完，我们把新的顶点（3）加入到了集合S中，那么不在集合S中的点到集合S中的点的距离就应该更新。举个例子：

• 在点（3）没加入集合S前，S=0，点（5）到集合S的最小距离为无穷大，dis[5]=MAX
• 在点（3）加入集合S后，S=0,3，点（5）到集合S的最小距离就是点（3）到点（5）的距离，dis[5]=6

除此之外我们还应当记录下close[5]=3，表示点（3）作为点（5）到S中的最近邻点

//每一次循环用于在index加入S后，重新计算不在S中的顶点到S的距离，修改与index相邻的边
//到S的距离，即更新dis和close
    for(int k=0;k<n;++k) 
        //松弛操作，如果k没有被使用，且k到index的距离比原来k到S的距离小
        if(visited[k]==0&&dis[k]>e[index][k]) 
            dis[k]=e[index][k];//将k到index的距离作为新的k到S之间的距离
            close[k]=index;//将index作为k在S中的最近邻点
        
    

然后就套用一个循环，从点（1）找到点（n）；不多说了直接看图

找到第四个点：

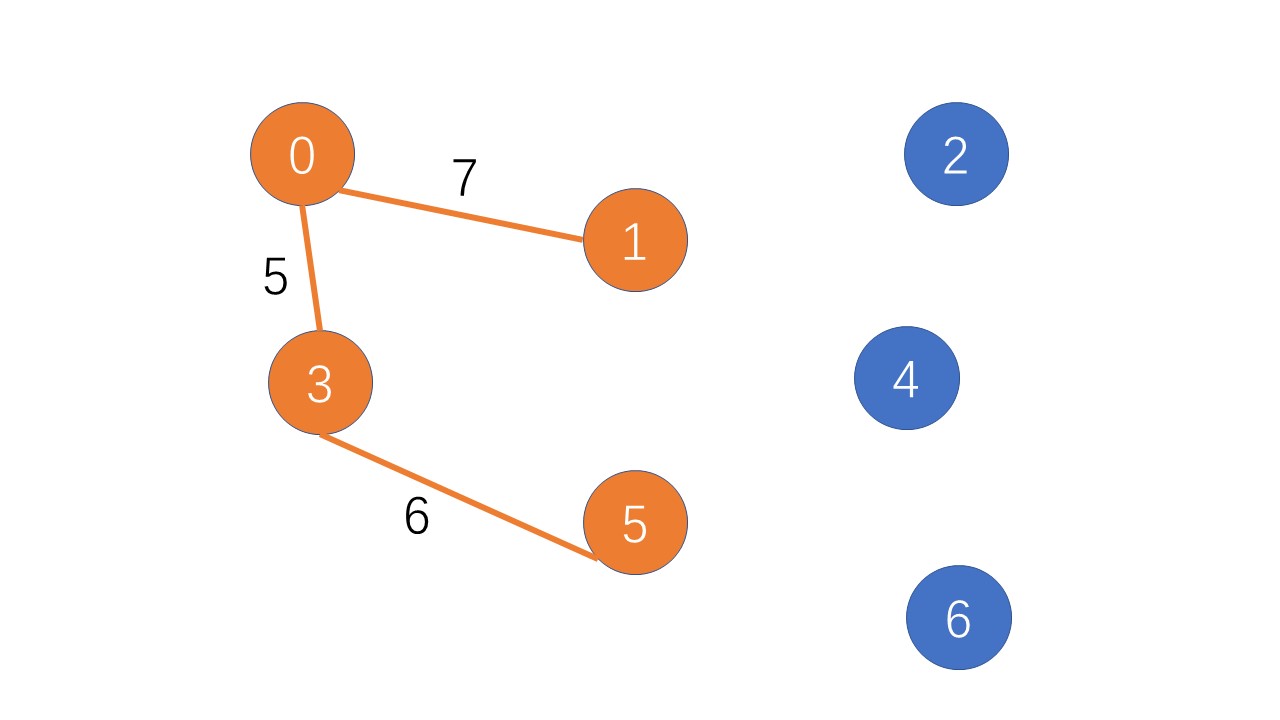
找到第五个点：

找到第六个点：

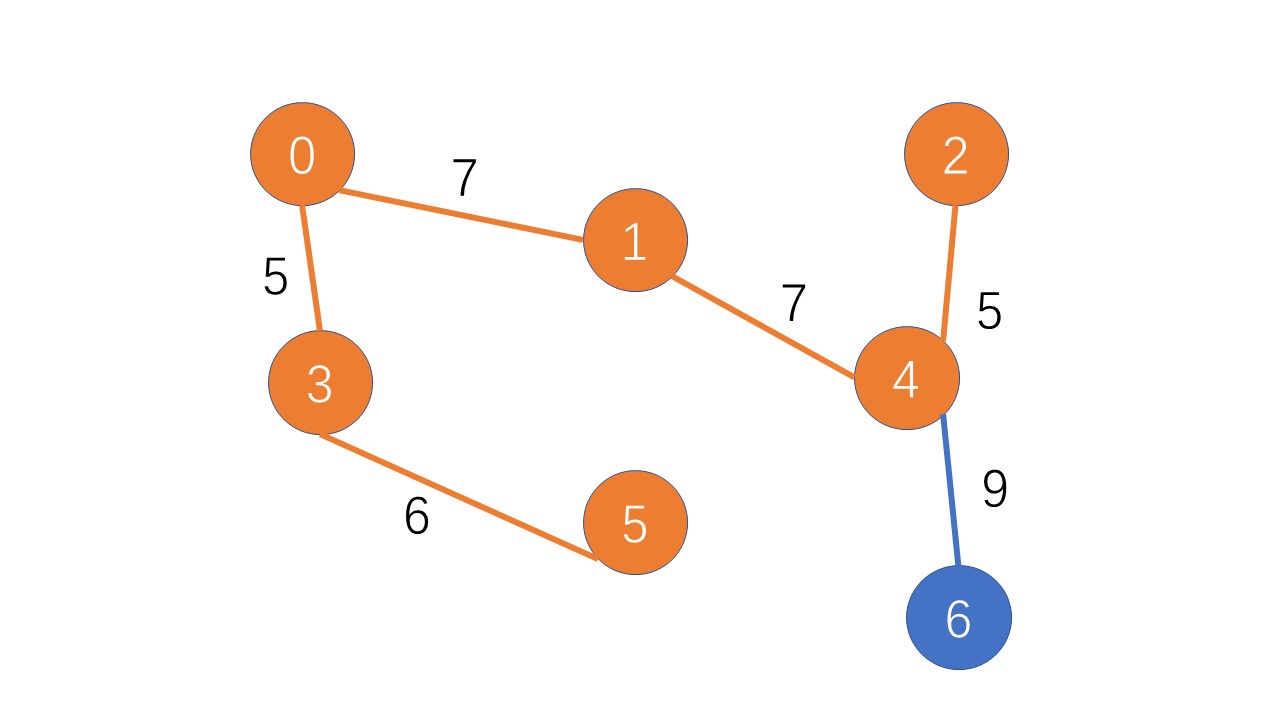
找到第七个点：找全啦，正好7-1=6条边

5.完整代码

import java.util.Scanner;
public class Main 

	public static void main(String[] args) 
		Scanner scanner=new Scanner(System.in);
		int n,m;//点和边
		int e[][];//储存权值
		int dis[];//记录最小权值
		int visited[];//记录当前点是否加入集合S
		int close[];//记录邻接点
		while(scanner.hasNext()) 
			n=scanner.nextInt();//点
			m=scanner.nextInt();//边
			e=new int[n][n];
			dis=new int[n];
			visited=new int[n];
			close=new int[n];
			
			//初始化各边均不相邻
			for(int i=0;i<n;++i) 
				for(int j=0;j<n;++j) 
					e[i][j]=Integer.MAX_VALUE;
				
			
			
			//录入各边的信息
			int x,y;
			for(int i=0;i<m;++i) 
				x=scanner.nextInt();
				y=scanner.nextInt();
				e[x][y]=scanner.nextInt();
				e[y][x]=e[x][y];//可别忘了这一行哦，无向图的存储
			
			
			//初始化，S中只有第1个点(0)
			for(int i=0;i<n;++i) 
				dis[i]=e[0][i];//获取其他顶点到第1个点(0)的距离，不直接相邻的顶点距离为无穷大
				close[i]=0;//初始情况下所有点的最近邻接点都为第1个点(0)
				visited[i]=0;//初始情况下所有点都没有被访问过
			
			visited[0]=1; //访问第1个点(0)，将第1个点加到S中
			
			for(int i=1;i<n;++i) 
				
				int index=0;
				//如果顶点k没有被使用，且到S的距
				//离小于k到S的距离，将k赋给index 
				for(int k=0;k<n;++k) 
					if(visited[k]==0&&dis[k]<dis[index]) 
						index=k;//记录到S距离最小的顶点
					
				
				//输出构成最小生成树的每条边
				System.out.println(close[index]+" "+index+" "+dis[index]);
				
				//将顶点index加入集合S并更新dis[]数组
				visited[index]=1;
				
				//每一次循环用于在index加入S后，重新计算不在S中的顶点到S的距离，修改与index相邻的边
				//到S的距离，即更新dis和close
				for(int k=0;k<n;++k) 
					//松弛操作，如果k没有被使用，且k到index的距离比原来k到S的距离小
					if(visited[k]==0&&dis[k]>e[index][k]) 
						dis[k]=e[index][k];//将k到index的距离作为新的k到S之间的距离
						close[k]=index;//将index作为k在S中的最近邻点
					
				
			
		
		scanner.close();
	

测试案例：

7 11
0 1 7
0 3 5
1 2 8
1 3 9
1 4 7
2 4 5
3 4 15
3 5 6
4 5 8
4 6 9
5 6 11

样例输出：

0 3 5
3 5 6
0 1 7
1 4 7
4 2 5
4 6 9

最小生成树算法Kruskal算法Prim算法切分定理贪心算法

最小生成树算法

生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。

最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。 

 

Kruskal算法

此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。 1. 把图中的所有边按代价从小到大排序； 2. 把图中的n个顶点看成独立的n棵树组成的森林； 3. 按权值从小到大选择边，所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。 4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

 

 

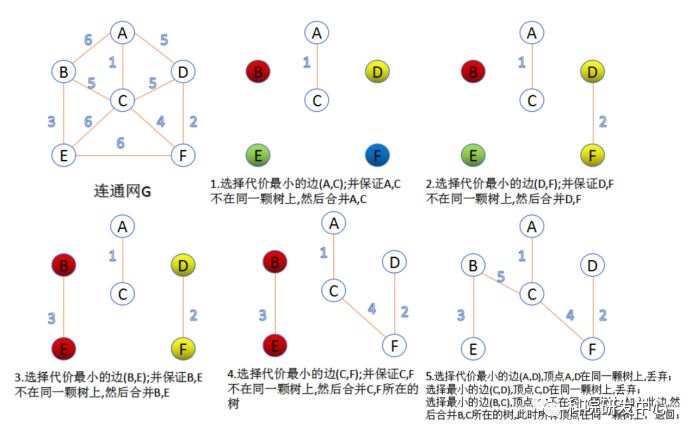
Prim算法

此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

1. 图的所有顶点集合为VV；初始令集合u={s},v=V−uu={s},v=V−u;

2. 在两个集合u,vu,v能够组成的边中，选择一条代价最小的边(u0,v0)(u0,v0)，加入到最小生成树中，并把v0v0并入到集合u中。

3. 重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

由于不断向集合u中加点，所以最小代价边必须同步更新；需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息，：

 

切分定理

 

贪心算法

贪心算法总是作出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑，它所作出的选择只是在某种意义上的局部最优选择。

当然，希望贪心算法得到的最终结果也是整体最优的。虽然贪心算法不能对所有问题都得到整体最优解，但对许多问题它能产生整体最优解。

如单源最短路经问题，最小生成树问题等。在一些情况下，即使贪心算法不能得到整体最优解，其最终结果却是最优解的很好近似