Mybatis-Plus-通俗易懂全讲解
Posted qq_55293923
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Mybatis-Plus-通俗易懂全讲解相关的知识,希望对你有一定的参考价值。
Mybatis-Plus
简介
MyBatis-Plus (opens new window)(简称 MP)是一个 MyBatis (opens new window)的增强工具,在 MyBatis 的基础上只做增强不做改变,为简化开发、提高效率而生。
详情见官网:https://baomidou.com/pages/24112f/#%E7%89%B9%E6%80%A7
快速入门
- 建表
DROP TABLE IF EXISTS user;
CREATE TABLE user
(
id BIGINT(20) NOT NULL COMMENT '主键ID',
name VARCHAR(30) NULL DEFAULT NULL COMMENT '姓名',
age INT(11) NULL DEFAULT NULL COMMENT '年龄',
email VARCHAR(50) NULL DEFAULT NULL COMMENT '邮箱',
PRIMARY KEY (id)
);
DELETE FROM user;
INSERT INTO user (id, name, age, email) VALUES
(1, 'Jone', 18, 'test1@baomidou.com'),
(2, 'Jack', 20, 'test2@baomidou.com'),
(3, 'Tom', 28, 'test3@baomidou.com'),
(4, 'Sandy', 21, 'test4@baomidou.com'),
(5, 'Billie', 24, 'test5@baomidou.com');
- 创建一个空的Spring Boot工程
- 添加依赖mysql,lombok,mybatis_plus
<dependency>
<groupId>mysql</groupId>
<artifactId>mysql-connector-java</artifactId>
<version>8.0.28</version>
</dependency>
<dependency>
<groupId>org.projectlombok</groupId>
<artifactId>lombok</artifactId>
<version>1.18.22</version>
</dependency>
<dependency>
<groupId>com.baomidou</groupId>
<artifactId>mybatis-plus-boot-starter</artifactId>
<version>3.5.1</version>
</dependency>
- 编写配置文件,连接数据库
spring.datasource.username=root
spring.datasource.password=123456
spring.datasource.url=jdbc:mysql://localhost:3306/mybatis_plus?useSSL=true&useUnicode=true&characterEncoding=utf-8&serverTimezone=GMT%2B8
spring.datasource.driver-class-name=com.mysql.cj.jdbc.Driver
5. 传统方式pojo-dao(连接mybatis,配置mapper.xml文件)-service-controller
5. 使用了mybatis-plus之后(继承BaseMapper接口,省略了mapper.xml文件)
- pojo
@Data
@AllArgsConstructor
@NoArgsConstructor
public class User
private Long id;
private String name;
private Integer age;
private String email;
- mapper接口
//在对应的mapper上面继承基本接口就可以 BaseMapper
@Repository//代表持久层
public interface UserMapper extends BaseMapper<User>
//所有的CRUD操作都已经编写完成了
//你不需要像以前一样配置一大堆文件了
- 注意点,我们需要在主启动类上去扫描我们mapper包下的所有接口
@MapperScan("com.kuang.mapper")
//扫描我们的mapper文件夹
@MapperScan("com.kuang.mapper")
@SpringBootApplication
public class MybatisPlusApplication
public static void main(String[] args)
SpringApplication.run(MybatisPlusApplication.class, args);
- 测试类中测试
@SpringBootTest
class MybatisPlusApplicationTests
//继承了BaseMapper,所有方法都来自父类,我们也可以编写自己的拓展方法
@Autowired
private UserMapper userMapper;
@Test
void contextLoads()
//这里的参数是一个Wrapper,条件构造器,这里我们先不用,将其设为null
//查询全部用户
List<User> userList = userMapper.selectList(null);
userList.forEach(System.out::println);
思考问题
- SQL谁帮我们写的?MyBatis-Plus
- 方法哪里来的?MyBatis-Plus
配置日志
我们所有的sql现在是不可见的,我们希望知道它是怎么执行的,所以我们必须要看日志!
# 配置日志
mybatis-plus.configuration.log-impl=org.apache.ibatis.logging.stdout.StdOutImpl
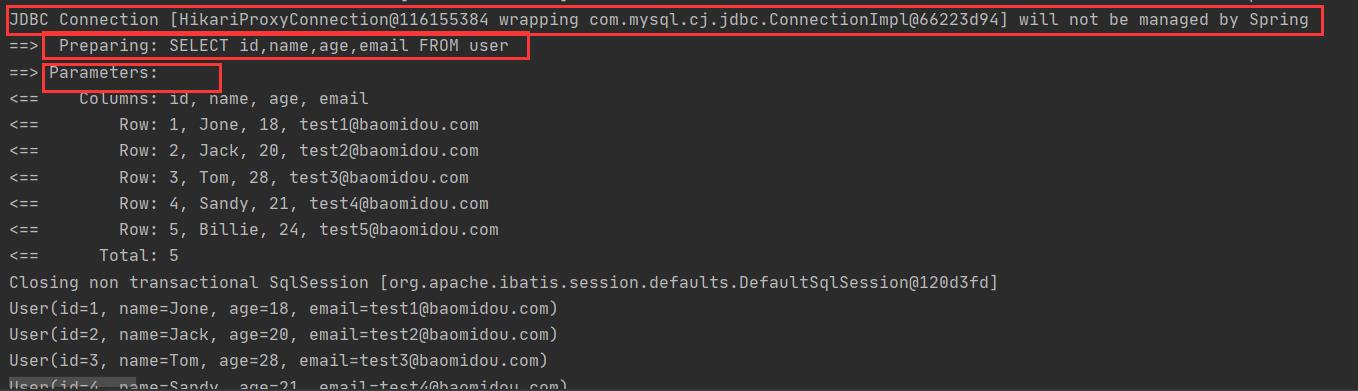
配置完毕日志之后,后面的学习就需要注意这个自动生成的SQL,你们就会喜欢上Mybatis-Plus!
CRUD扩展
插入操作
insert插入
@Test//测试插入
public void textInsert()
User user = new User();
user.setName("lala啦");
user.setAge(3);
user.setEmail("465386@qq.com");
int result = userMapper.insert(user);//帮我们自动生成id
System.out.println(result);//受影响的行数
System.out.println(user);//发现,id会自动回填

数据库插入的id的默认值为:全局的唯一id
主键生成策略
默认ASSIGN_ID全局唯一id
分布式系统唯一id生成:https://www.cnblogs.com/haoxinyue/p/5208136.html
雪花算法:
snowflake是Twitter开源的分布式ID生成算法,结果是一个long型的ID。其核心思想是∶使用41bit作为毫秒数,10bit作为机器的ID( 5个bit是数据中心,5个bit的机器ID),12bit作为毫秒内的流水号(意味着每个节点在每毫秒可以产生4096个ID),最后还有一个符号位,永远是0。可以保证几乎全球唯一!
主键自增
我们需要配置主键自增:
- 实体类字段上
@TableId(type = IdType.AUTO) - 数据库字段一定要是自增的!
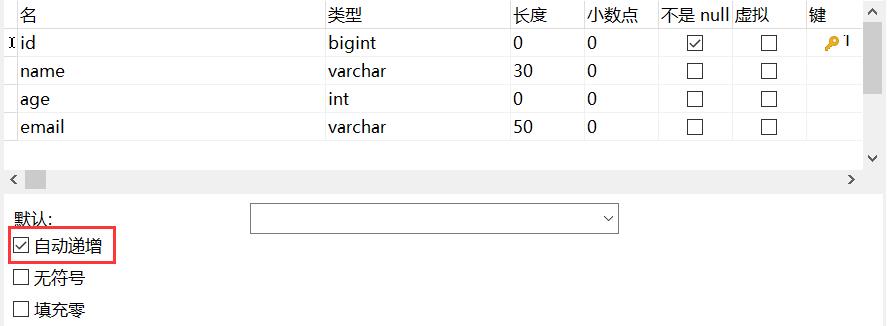
- 再次测试插入即可,并且自增量为1!
其余IdType的源码解释
public enum IdType
AUTO(0),//数据库id自增
NONE(1),//未设置主键
INPUT(2),//手动输入,就需要自己配置id了
ASSIGN_ID(3),//默认的全局唯一id
ASSIGN_UUID(4);//全局唯一id
更新操作
@Test
//测试更新
public void testUpdate()
User user = new User();
//通过条件自动拼接动态sql
user.setId(6L);
user.setName("lala嘿嘿");
user.setAge(3);
user.setEmail("111111@qq.com");
//注意:userById 但是参数是一个对象
int i = userMapper.updateById(user);
System.out.println(i);

所有的sql都是自动帮你动态配置的!
自动填充
创建时间、修改时间!这些个操作都是自动化完成的,我们不希望手动更新!
阿里巴巴开发手册:所有的数据库表:gmt_create、gmt_modified几乎所有的表都要配置上!而且需要自动化!
方式一:数据库级别(工作中不允许你修改数据库)
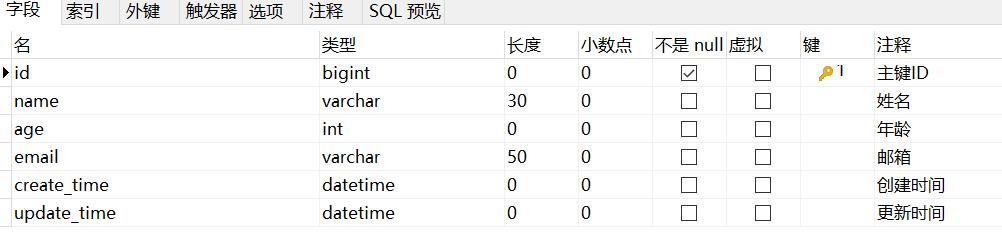
- 在表中新增字段create_time,update_time
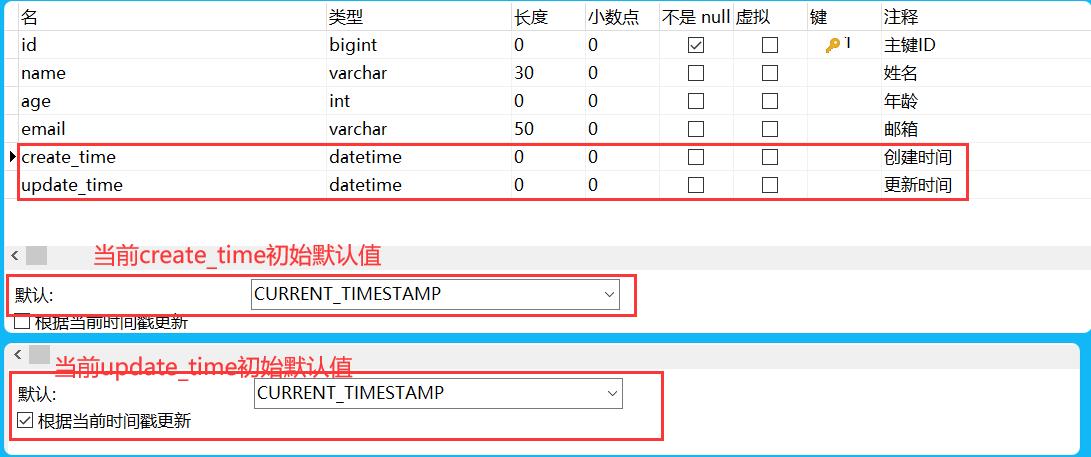
- 再次测试插入方法,我们需要先把实体类同步!
private Date createTime;
private Date updateTime;
- 再次更新查看结果即可
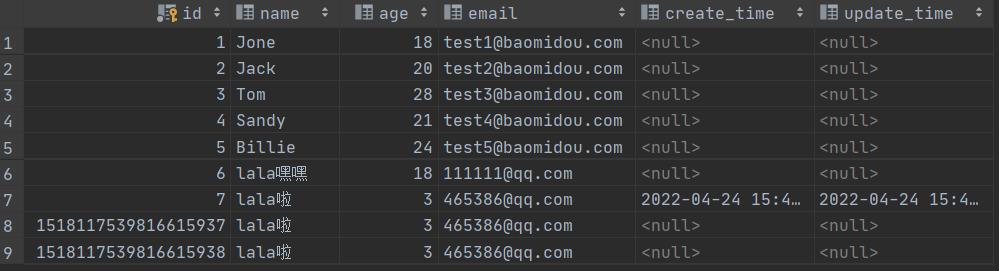
出现问题:除了插入记录,其余创建时间和更新时间都为null
解决问题:在建字段的时候,需要设置该字段不能为空
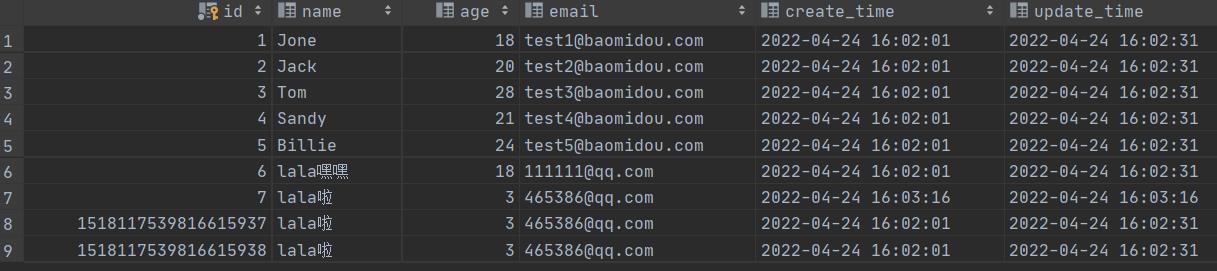
方式二:代码级别
- 删除数据库中create_time,update_time这两个字段的默认值、update_time更新操作
- 实体类字段属性上需要增加注解
//字段添加填充内容
//插入的时候填充字段
@TableField(fill = FieldFill.INSERT)
private Date createTime;
//插入和更新的时候填充字段
@TableField(fill = FieldFill.INSERT_UPDATE)
private Date updateTime;
- 编写处理器来处理这个注解即可!
@Slf4j//对日志依赖的引用
@Component//一定不要忘记把处理器增加到IOC容器中!
public class MyMetaObjectHandler implements MetaObjectHandler
//插入时的填充策略
@Override
public void insertFill(MetaObject metaObject)
log.info("start insert fill......");
this.setFieldValByName("createTime",new Date(),metaObject);
//MetaObject[反射对象类]是Mybatis的工具类,通过MetaObject获取和设置对象的属性值。
this.setFieldValByName("updateTime",new Date(),metaObject);
//更新时的填充策略
@Override
public void updateFill(MetaObject metaObject)
log.info("start update fill.....");
this.setFieldValByName("updateTime",new Date(),metaObject);
- 测试插入
- 测试更新、观察时间即可
- 小结:但是有一点,我发现其他记录没有默认的创建create_time,update_time这两个字段,只有进行了插入或更新的字段这两个字段才会填充
乐观锁
乐观锁:顾名思义十分乐观,它总是认为不会出现问题,无论干什么不去上锁!如果出现了问题,就上锁,更新失败
悲观锁:顾名思义十分悲观,它总是认为会出现问题,无论干什么都会去上锁!再去操作
我们这里主要讲解 乐观锁机制!
乐观锁实现方式
- 取出记录时,获取当前version
- 更新时,带上这个version
- 执行更新时,set version = newVersion where version = oldVersion
- 如果version不对,就更新失败
【简而言之,就是持续更新,当发现版本不对时,也就是发现问题时,就上锁,更新失败】
//乐观锁:1.先查询,获得版本号 version = 1
--A
update user set name = "kuangshen" ,version = version + 1
where id = 2 and version = 1
--B 线程抢先完成,这个时候 version = 2,会导致 A 修改失败!
update user set name = "kuangshen" ,version = version + 1
where id = 2 and version = 1
测试一下Mybatis- Plus的乐观锁插件
- 给数据库中增加version字段!
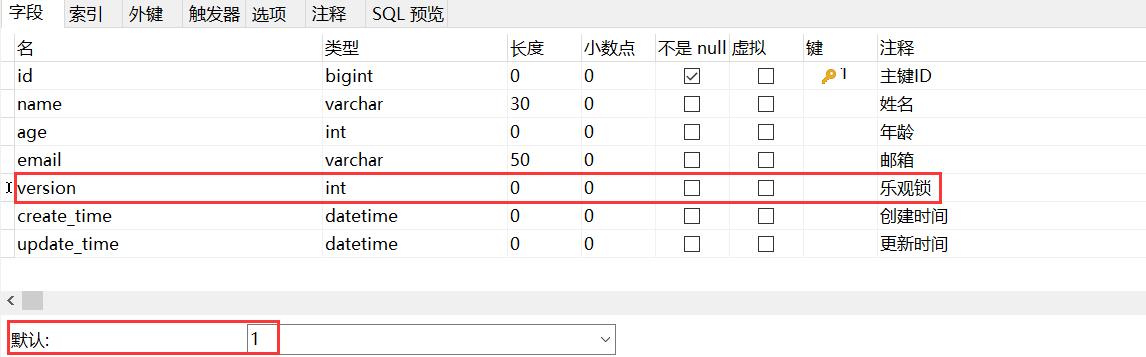
- 我们实体类要加对应的字段
@Version//乐观锁Version注解
private Integer version;
- 注册组件
//扫描我们的mapper文件夹
@MapperScan("com.kuang.mapper")
@EnableTransactionManagement//自动管理事务开启,默认也是开启的
@Configuration//这是一个配置类
public class MybatisPlusConfig
//注册乐观锁插件
@Bean
public MybatisPlusInterceptor mybatisPlusInterceptor()
MybatisPlusInterceptor interceptor = new MybatisPlusInterceptor();
interceptor.addInnerInterceptor(new OptimisticLockerInnerInterceptor());
return interceptor;
- 测试一下
//测试乐观锁成功
@Test
public void testOptimisticLocker()
//1.查询
User user = userMapper.selectById(1L);
//2.修改,它很乐观它觉得这个用户没有问题,,进行修改
user.setName("呀嘿");
user.setEmail("5555555@qq.com");
user.setAge(2);
//3.执行更新操作
userMapper.updateById(user);
//测试乐观锁失败
@Test
public void testOptimisticLocker2()
//线程一
User user = userMapper.selectById(1L);
user.setName("yiyi嘿11");
user.setEmail("111111@qq.com");
//模拟另外一个线程执行了插队操作
User user2 = userMapper.selectById(1L);
user2.setName("yi嘿哈22");
user2.setEmail("222222@qq.com");
userMapper.updateById(user2);
//自旋锁来多次尝试提交!
userMapper.updateById(user);//如果没有乐观锁就会覆盖插队线程的值!
自旋锁(拓展)
“自旋”就是自己在这里不停地循环,直到目标达成。而不像普通的锁那样,如果获取不到锁就进入阻塞
查询操作
//测试批量查询!
@Test
public void testSelectByBatchId()
List<User> users = userMapper.selectBatchIds(Arrays.asList(1, 2, 3));
users.forEach(System.out::println);
//按条件查询之一使用 map 操作
@Test
public void testSelectByBatchIds()
HashMap<String, Object> map = new HashMap<>();
//自定义要查询
map.put("name","Jack");
List<User> users = userMapper.selectByMap(map);
users.forEach(System.out::println);
分页查询
分页在网站使用的十分之多!
- 原始的limit进行分页
- pageHelper第三方插件
- MP其实也内置了分页插件!
如何使用!
- 配置拦截器组件即可
@Bean
public MybatisPlusInterceptor mybatisPlusInterceptor()
MybatisPlusInterceptor interceptor = new MybatisPlusInterceptor();
//分页插件
interceptor.addInnerInterceptor(new PaginationInnerInterceptor(DbType.H2));
//乐观锁插件
interceptor.addInnerInterceptor(new OptimisticLockerInnerInterceptor());
return interceptor;
- 直接使用Page对象即可!
//测试分页查询
@Test
public void testPage()
//参数一:当前页
//参数二:页面大小
//使用了分页插件后,所有的分页操作也变得简单了
IPage page = new Page<>(2, 5);
userMapper.selectPage(page,null);
page.getRecords().forEach(System.out::println);
System.out.println(page.getTotal());
删除操作
基本的删除操作
//测试删除
//通过id
@Test
public void testDeleteById()
userMapper.deleteById(1518117539816615937L);
//通过id批量删除
@Test
public void testDeleteBatchIds()
userMapper.deleteBatchIds(Arrays.asList(1518117539816615938L,8L));
//通过map删除
@Test
public void testDeleteMap()
HashMap<String, Object> map = new HashMap<>();
map.put("name","yi嘿哈22");
userMapper.deleteByMap(map);
我们在工作中会遇到一些问题:逻辑删除!
逻辑删除
物理删除:从数据库中直接移除
逻辑删除:在数据库中没有被移除,而是通过一个变量来让他失效!delete = 0>>delete=1
管理员可以查看被删除的记录!防止数据的丢失,类似于回收站!
测试一下:
- 在数据表中增加一个delete字段

- 实体类中增加属性
@TableLogic//逻辑删除
private Integer deleted;
- 配置!
例: application.yml
mybatis-plus:
global-config:
db-config:
logic-delete-field: flag # 全局逻辑删除的实体字段名(since 3.3.0,配置后可以忽略不进行@TableLogic注解)
logic-delete-value: 1 # 逻辑已删除值(默认为 1)
logic-not-delete-value: 0 # 逻辑未删除值(默认为 0)
- 测试一下删除
执行的是update操作不是delete操作

数据没有被删除,只是deleted字段值被标记为1

查询的时候会自动拼接deleted,加上deleted=0的条件

CRUD小结
以上的所有CRUD操作极其拓展操作,我们都必须精通掌握!会大大提高你的工作和写项目的效率!
注意:以上操作仅供参考,根据版本不同和更新较快,主要以Mybatis-Plus官网内容为主,其内容也较好阅读。
性能分析插件
作用:性能分析拦截器,用于输出每条SQL语句极其执行时间
如果超过这个时间就停止运行
由于MP此版本较新,官网已经没有了MP性能分析插件,所以此处用了第三方p6spy插件
1.导入pom相关依赖
<!--mybatis-plus-->
<dependency>
<groupId>com.baomidou</groupId>
<artifactId>mybatis-plus-boot-starter</artifactId>
<version>3.5.1</version>
</dependency>
<!--执行 SQL 分析打印插件-->
<dependency>
<groupId>p6spy</groupId>
<artifactId>p6spy</artifactId>
<version>3.8.1</version>
</dependency>
<!--mybatis-plus代码生成器-->
<dependency>
<groupId>com.baomidou</groupId>
<artifactId>mybatis-plus-generator</artifactId>
<version>3.5.1</version>
</dependency>
2.修改 application.yml
### 默认配置如下
spring:
datasource:
driver-class-name: com.mysql.cj.jdbc.Driver
url: jdbc:mysql://localhost:3306/mybatis_plus?useUnicode=true&characterEncoding=utf8&useSSL=false&useLegacyDatetimeCode=false&serverTimezone=GMT%2b8&tinyInt1isBit=true
username: root
password: 123456
### 修改配置如下
spring:
datasource:
driver-class-name: com.p6spy.engine.spy.P6SpyDriver
url: jdbc:p6spy:mysql://localhost:3306/mybatis?useUnicode=true&characterEncoding=utf8&useSSL=false&useLegacyDatetimeCode=false&serverTimezone=GMT%2b8&tinyInt1isBit=true
3.在项目的resources下添加"spy.properties" p6spy的位置文件
modulelist=com.baomidou.mybatisplus.extension.p6spy.MybatisPlusLogFactory,com.p6spy.engine.outage.P6OutageFactory
# 自定义日志打印
logMessageFormat=com.baomidou.mybatisplus.extension.p6spy.P6SpyLogger
#日志输出到控制台
appender=com.baomidou.mybatisplus.extension.p6spy.StdoutLogger
# 使用日志系统记录 sql
#appender=com.p6spy.engine.spy.appender.Slf4JLogger
# 设置 p6spy driver 代理
deregisterdrivers=true
# 取消JDBC URL前缀
useprefix=true
# 配置记录 Log 例外,可去掉的结果集有error,info,batch,debug,statement,commit,rollback,result,resultset.
excludecategories=info,debug,result,commit,resultset
# 日期格式
dateformat=yyyy-MM-dd HH:mm:ss
# 实际驱动可多个
#driverlist=org.h2.Driver
# 是否开启慢SQL记录
outagedetection=true
# 慢SQL记录标准 2 秒
outagedetectioninterval=2
4.执行查询接口
控制台会显示如下代码
Consume Time:20 ms 2020-06-30 09:26:25
Execute SQL:SELECT ID, NAME, AGE, SEX, date_format( INPUT_DATE, '%Y-%c-%d %h:%i:%s' ) inputDate FROM student where 1=1 LIMIT 10
使用性能分析插件,可以帮助我们提高效率!
条件构造器
十分重要
我们写一些复杂的sql就可以用它来代替
1.测试一,记住查看输出的SQL进行分析
@Test
void contextLoads()
//查询name不为空,邮箱不为空的用户,年龄大于等于24
QueryWrapper<User> wrapper = new QueryWrapper<>();//和mapper很像,但是wrapper是一个对象,不用put,而是去用方法
wrapper
.isNotNull("name")
.isNotNull("email")
.ge("age",24);
userMapper.selectList(wrapper).forEach(System.out::println);

2.测试二,记住查看输出的SQL进行分析
@Test
void contextLoads2()
//查询名字为Tom的
QueryWrapper<User> wrapper = new QueryWrapper<>();
wrapper.eq("name","Tom");
User user = userMapper.selectOne(wrapper);//查询一个数据,出现多个结果使用List或者Map
System.out.println(user);
3.测试三,记住查看输出的SQL进行分析
@Test
void contextLoads3()
//查询年龄在20-30之间的用户
QueryWrapper<User> wrapper = new QueryWrapper<>();
wrapper.between("age",20,30);//区间,不包括20和30
Long count = userMapper.selectCount(wrapper);//查询结果数量
System.out.println(count);
4.测试四,记住查看输出的SQL进行分析
//模糊查询
@Test
void contextLoads4()
QueryWrapper&通俗易懂讲解梯度下降法!
Datawhale干货
作者:知乎King James,伦敦国王大学
知乎 | https://zhuanlan.zhihu.com/p/335191534
前言:入门机器学习必须了解梯度下降法,虽然梯度下降法不直接在机器学习里使用,但是它的思维方式是后续学习其他算法的基础。网上已有的文章要么整一堆数学公式,要么就是简单草草了事。本篇文章用讲解+实战的形式,浅显易懂讲解,拥有高中数学知识即可看懂。
1. 引入
我们先从一个案例入手,下图是一组上海市静安区的房价信息

别看了,数据我瞎编的,上海静安的房价不可能这么便宜
我们用Python在坐标系上面画出来如下图:

我们现在想拟合一个线性函数来表示房屋面积和房价的关系。我们初中都学过的一元一次函数表达式为:y=kx+b(k≠0)。很明显不可能有一对组合(k,b)全部经过上图7个点,我们只能尽可能地找到一对组合,使得该线性函数离上图7个点的总距离最近。

如上图所示,实际值与预测值之间差异的均方差我们把它称为损失函数,也有叫做成本函数或者代价函数的,意义都一样。我们希望找到一个组合(k,b)可以使得损失函数的值最小。上述只有一个输入变量x,如果我们多加入几个输入变量,比如卧室的数量、离最近地铁站的距离。最终目标变量和损失函数我们用下述函数表达式来表达:

现在我们的任务就是求出一组θ,在已知【x,y】的前提下使得损失函数的值最小。那么如何计算出θ了,使用什么方法?
我们首先回到损失函数表达式本身,损失函数本身是一个y=x^2的形式,高中数学大家应该都学过这是一个开口向上的抛物线方程,大概长下图这样:
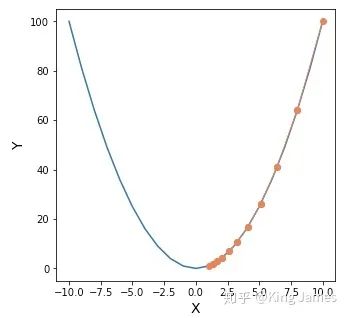
我们如何找到这个函数的最低点?上图是一个二维图,我们很轻松就可以肉眼看出x=0时,y最小。如果维度更多,比如z = (x-10)^2 + (y-10)^2,则得到下图:

我们如何定位出最小值,特别强调一点,这里的x是一个“大”参数的概念,x应该等于下述公式
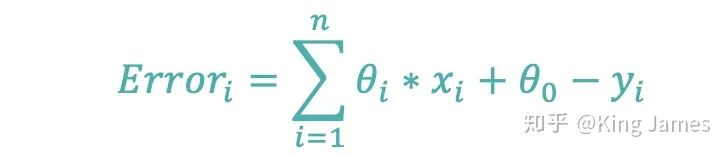
大家要明确上图横坐标是x和y,函数表达式里的θ已经知道了,所以我们是找到最合适的(x,y)使得函数值最小。如果我们现在是已知样本(x,y),那么上图的变量就变为了θ_0和θ_i,并不是x_i,我们是以θ_0和θ_i作为输入变量做的图,x_i和y_i都是已知的固定值,这一点必须明确了。上图的纵坐标的值就变为损失函数的值。
我们的问题是已知样本的坐标(x,y),来求解一组θ参数,使得损失函数的值最小。我们如何找到上图中的最低点?因为找到最低点,那么最低点对应的横坐标所有维度就是我们想得到的θ_0和θ_i,而纵坐标就是损失函数的最小值。找到最低点所有答案就全部解出来了。
现在问题来了:有没有一种算法让我们可以慢慢定位出最小值?这个算法就是梯度下降法。
2. 梯度下降法简介
2.1 梯度下降法的思想
我们首先介绍梯度下降法的整体思想。假设你现在站在某个山峰的峰顶,你要在天黑前到达山峰的最低点,那里有食品水源供给站,可以进行能量补充。你不需要考虑下山的安全性,即使选择最陡峭的悬崖下山,你也可以全身而退,那么如何下山最快?
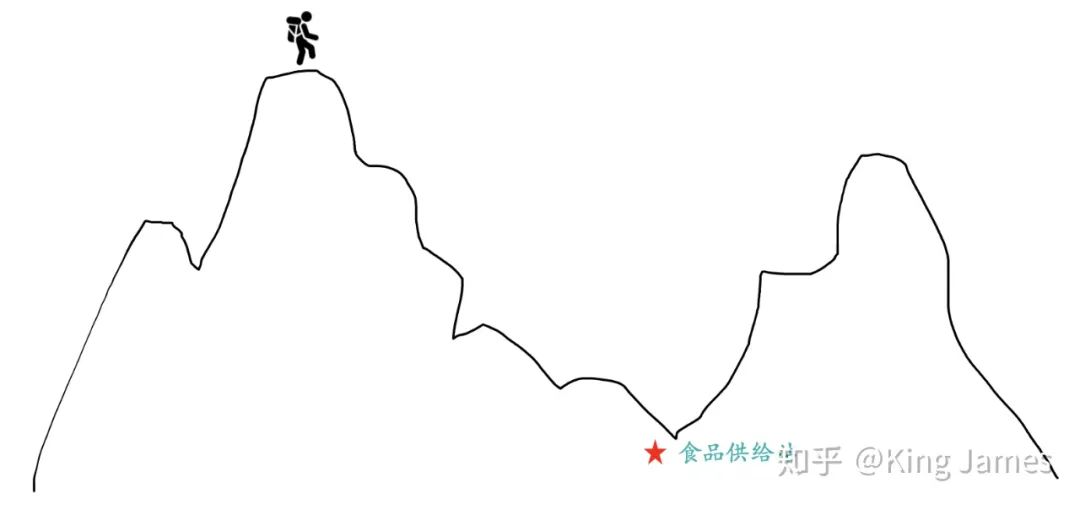
最快的方法就是以当前的位置为基准,寻找该位置最陡峭的地方,然后沿该方向往下走。走一段距离后,再以当前位置为基准,重新寻找最陡峭的地方,一直重复最终我们就可以到达最低点。我们需要不停地去重新定位最陡峭的地方,这样才不会限于局部最优。
那么整个下山过程中我们会面临两个问题:
如何测量山峰的“陡峭”程度;
每一次走多长距离后重新进行陡峭程度测量;走太长,那么整体的测量次数就会比较少,可能会导致走的并不是最佳路线,错过了最低点。走太短,测量次数过于频繁,整体耗时太长,还没有到达食品供给站就已经GG了。这里的步长如何设置?

三种不同步长可能导致的后果
Part1里面介绍了如何从一个开口向上的抛物线高点定位到最低点的问题,这个和下山的场景是完全类似的。
抛物线就相当于一个山峰,我们的目标就是找到抛物线的最低点,也就是山底。最快的下山方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到抛物线中,就是计算给定点的梯度,然后朝着梯度相反的方向( Part 2.3里面会解释为什么是朝着梯度相反的方向),就能让抛物线值下降的最快。同时我们也要和下山一样,不停地定位新位置,再计算新位置的梯度,然后按照新方向下降,最后慢慢定位到抛物线的最低点。
2.2 梯度下降法算法
Part2.1里面已经介绍了梯度下降法的思想,遗留了两个问题。第一就是如何计算“陡峭”程度,我们这里把它叫做梯度,我们用∇J_θ来代替。第二个也就是步长问题,我们用一个α学习率来代表这个步长,α越大代表步长越大。知道了这两个值,我们如何去得到θ参数的更新表达式?
J是关于θ的一个函数,假设初始时我们在θ_1这个位置,要从这个点走到J的最小值点,也就是山底。首先我们先确定前进的方向,也就是梯度的反向“-∇J_θ”,然后走一段距离的步长,也就是α,走完这个段步长,就到达了θ_2这个点了。表达式如下图:

我们按照上述表达式一直不停地更新θ的值,一直到θ收敛不变为止,当我们到达山底,此时函数的梯度就是0了,θ值也就不会再更新了,因为表达式的后半部分一直是0了。
整个下降过程中损失函数的值是一定在减少,但是我们想学习出来的参数值θ不一定一直在减小。因为我们需要找到损失函数最小时的坐标点,这个坐标点的坐标不一定是原点,很可能是(2,3)甚至是(4,6),我们找到的是最合适的θ值使得损失函数最小。下图我们用一个例子来进行说明:
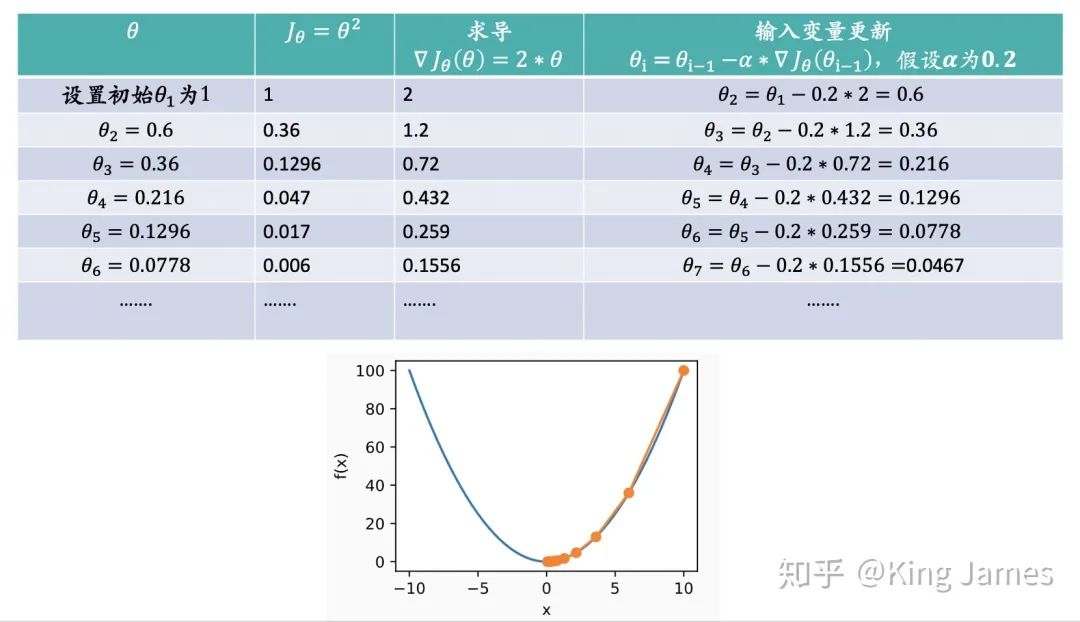
上图的最低点很明显就是原点,我们通过梯度下降法来逼近这个最低点。我们可以看到损失函数的值在一直减少,θ的值也在往0这个值进行收敛。
2.3 梯度下降法数学计算
Part2.1和2.2介绍了梯度下降的思想和θ更新的表达式,现在我们从数学层面进行解释:
为什么是向梯度相反的方向下降:
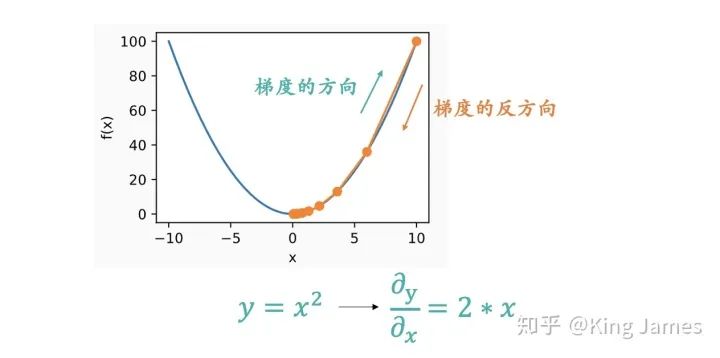
上图应该很形象地显示为什么要朝着梯度的反方向了。梯度是一个向量,梯度的方向是函数在指定点上升最快的方向,那么梯度的反方向自然是下降最快的方向了。
泛化的θ参数更新公式:
Part2.2里面的例子我们选择的是一个最简单的函数表达式,θ参数分为两种,一种是和输入变量x配对的参数θ_i,一种是固定的偏差θ_0。我们用已知的样本数据(x,y)来求解出使得损失函数最小的一组θ参数。下面我们来计算一个通用泛化的θ参数更新表达式。我们只需要用到高中数学中的导数知识即可,朋友们相信我真的很easy。
下图是对和输入变量x配对的参数θ_i更新表达式:

下图是对固定的偏差θ_0的更新表达式:

上面的数学过程也就是高中我们学习导数里面最简单的求导过程了。那么至此我们也就将梯度下降算法的思想和数学解释全部介绍完了。
2.4 梯度下降法分类
Part2.3里面的公式大家也看到了我们要借助样本的(x,y)的数据来进行参数θ的更新,如果现在样本有100条数据,我们如何来更新。正常情况下,我们更新的方式有两种:
随机梯度下降(Stochastic Gradient Descent)
我们每次只使用单个训练样本来更新θ参数,依次遍历训练集,而不是一次更新中考虑所有的样本。就像开头介绍那7条房价数据,我们一个一个来计算,计算一次更新一次θ,直到θ收敛或者达到后期更新幅度已经小于我们设置的阀值。
批量梯度下降(Batch Gradient Descent)
我们每次更新都遍历训练集中所有的样本,以它们的预测误差之和为依据更新。我们会一次性将7条样本数据的预测误差都汇总,然后进行一次更新。更新完以后,继续以7条样本数据的预测误差之和进行汇总,再更新,直到θ收敛或者达到后期更新幅度已经小于我们设置的阀值。
当训练样本数很大时,批量梯度下降的每次更新都会是计算量很大的操作,而随机梯度下降可以利用单个训练样本立即更新,因此随机梯度下降 通常是一个更快的方法。但随机梯度下降也有一个缺点,那就是θ可能不会收敛,而是在最小值附近振荡,但在实际中也都会得到一个足够好的近似。所以实际情况下,我们一般不用固定的学习率,而是让它随着算法的运行逐渐减小到零,也就是在接近“山底”的时候慢慢减小下降的“步幅”,换成用“小碎步”走,这样它就更容易收敛于全局最小值而不是围绕它振荡了。
3. 梯度下降法Python实践
以下代码全部使用Python3环境
3.1 单变量:y = x^2求最低点
import matplotlib.pyplot as plt
import numpy as np
# fx的函数值
def fx(x):
return x**2
#定义梯度下降算法
def gradient_descent():
times = 10 # 迭代次数
alpha = 0.1 # 学习率
x =10# 设定x的初始值
x_axis = np.linspace(-10, 10) #设定x轴的坐标系
fig = plt.figure(1,figsize=(5,5)) #设定画布大小
ax = fig.add_subplot(1,1,1) #设定画布内只有一个图
ax.set_xlabel('X', fontsize=14)
ax.set_ylabel('Y', fontsize=14)
ax.plot(x_axis,fx(x_axis)) #作图
for i in range(times):
x1 = x
y1= fx(x)
print("第%d次迭代:x=%f,y=%f" % (i + 1, x, y1))
x = x - alpha * 2 * x
y = fx(x)
ax.plot([x1,x], [y1,y], 'ko', lw=1, ls='-', color='coral')
plt.show()
if __name__ == "__main__":
gradient_descent()
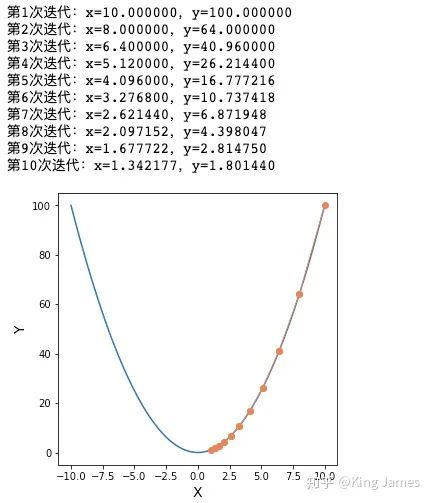
2D梯度下降图示
3.2 多变量求最低点
多变量:z = (x-10)^2 + (y-10)^2
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
#求fx的函数值
def fx(x, y):
return (x - 10) ** 2 + (y - 10) ** 2
def gradient_descent():
times = 100 # 迭代次数
alpha = 0.05 # 学习率
x = 20 # x的初始值
y = 20 # y的初始值
fig = Axes3D(plt.figure()) # 将画布设置为3D
axis_x = np.linspace(0, 20, 100)#设置X轴取值范围
axis_y = np.linspace(0, 20, 100)#设置Y轴取值范围
axis_x, axis_y = np.meshgrid(axis_x, axis_y) #将数据转化为网格数据
z = fx(axis_x,axis_y)#计算Z轴数值
fig.set_xlabel('X', fontsize=14)
fig.set_ylabel('Y', fontsize=14)
fig.set_zlabel('Z', fontsize=14)
fig.view_init(elev=60,azim=300)#设置3D图的俯视角度,方便查看梯度下降曲线
fig.plot_surface(axis_x, axis_y, z, rstride=1, cstride=1, cmap=plt.get_cmap('rainbow')) #作出底图
for i in range(times):
x1 = x
y1 = y
f1 = fx(x, y)
print("第%d次迭代:x=%f,y=%f,fxy=%f" % (i + 1, x, y, f1))
x = x - alpha * 2 * (x - 10)
y = y - alpha * 2 * (y - 10)
f = fx(x, y)
fig.plot([x1, x], [y1, y], [f1, f], 'ko', lw=2, ls='-')
plt.show()
if __name__ == "__main__":
gradient_descent()
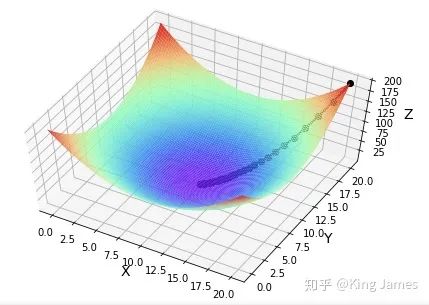
3.3 根据给定样本求解出最佳θ组合
import numpy as np
import matplotlib.pyplot as plt
#样本数据
x = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
y = [3,4,5,5,2,4,7,8,11,8,10,11,13,13,16,17,16,17,18,20]
m = 20 #样本数量
alpha = 0.01#学习率
θ_0 = 1 #初始化θ_0的值
θ_1 = 1 #初始化θ_1的值
#预测目标变量y的值
def predict(θ_0,θ_1, x):
y_predicted = θ_0 + θ_1*x
return y_predicted
#遍历整个样本数据,计算偏差,使用批量梯度下降法
def loop(m,θ_0,θ_1,x,y):
sum1 = 0
sum2 = 0
error = 0
for i in range(m):
a = predict(θ_0,θ_1, x[i]) - y[i]
b = (predict(θ_0,θ_1, x[i]) - y[i])* x[i]
error1 = a*a
sum1 = sum1 + a
sum2 = sum2 + b
error = error + error1
return sum1,sum2,error
#批量梯度下降法进行更新θ的值
def batch_gradient_descent(x, y,θ_0,θ_1, alpha,m):
gradient_1 = (loop(m,θ_0,θ_1,x,y)[1]/m)
while abs(gradient_1) > 0.001:#设定一个阀值,当梯度的绝对值小于0.001时即不再更新了
gradient_0 = (loop(m,θ_0,θ_1,x,y)[0]/m)
gradient_1 = (loop(m,θ_0,θ_1,x,y)[1]/m)
error = (loop(m,θ_0,θ_1,x,y)[2]/m)
θ_0 = θ_0 - alpha*gradient_0
θ_1 = θ_1 - alpha*gradient_1
return(θ_0,θ_1,error)
θ_0 = batch_gradient_descent(x, y,θ_0,θ_1, alpha,m)[0]
θ_1 = batch_gradient_descent(x, y,θ_0,θ_1, alpha,m)[1]
error = batch_gradient_descent(x, y,θ_0,θ_1, alpha,m)[2]
print ("The θ_0 is %f, The θ_1 is %f, The The Mean Squared Error is %f " %(θ_0,θ_1,error))
plt.figure(figsize=(6, 4))# 新建一个画布
plt.scatter(x, y, label='y')# 绘制样本散点图
plt.xlim(0, 21)# x轴范围
plt.ylim(0, 22)# y轴范围
plt.xlabel('x', fontsize=20)# x轴标签
plt.ylabel('y', fontsize=20)# y轴标签
x = np.array(x)
y_predict = np.array(θ_0 + θ_1*x)
plt.plot(x,y_predict,color = 'red')#绘制拟合的函数图
plt.show()
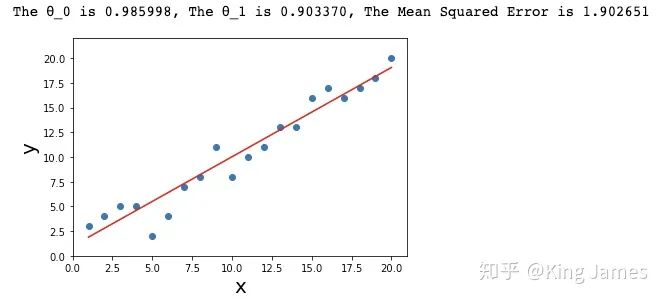
本篇文章前半部分通俗易懂地将整个梯度下降算法全面地讲解了一遍,后半部分通过Python将整个算法实现了一遍,大家可自行下载运行,欢迎大家沟通交流~
参考资料:
https://zhuanlan.zhihu.com/p/107782332 https://www.jianshu.com/p/c7e642877b0e https://www.jiqizhixin.com/articles/2019-04-07-6

King James
伦敦国王学院 数据科学硕士
知乎同名

整理不易,点赞三连↓
以上是关于Mybatis-Plus-通俗易懂全讲解的主要内容,如果未能解决你的问题,请参考以下文章