Intel Code Challenge Final Round (Div. 1 + Div. 2, Combined)题解报告

Posted 2022-07-31 queuelovestack

此文章可以使用目录功能哟↑(点击上方[+])

再一次卡在C题上,考查的居然是初中的科学知识,不过能涨一波分也是蛮开心的...

链接→Intel Code Challenge Final Round (Div. 1 + Div. 2, Combined)

 Problem A-Checking the Calendar

Accept: 0    Submit: 0
Time Limit: 1 second    Memory Limit : 256 megabytes

 Problem Description

You are given names of two days of the week.

Please, determine whether it is possible that during somenon-leap year the first day of some month was equal to the first day of the week you are given, while the first day ofthe next month was equal to the second day of the week you are given.Both months should belong to one year.

In this problem, we consider the Gregorian calendar to be used. The number of months in this calendar is equal to 12. The number of days in months during any non-leap year is: 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31.

Names of the days of the week are given with lowercase English letters: "monday", "tuesday", "wednesday", "thursday", "friday", "saturday", "sunday".

 Input

The input consists of two lines, each of them containing the name of exactly one day of the week. It's guaranteed that each string in the input is from the set "monday", "tuesday", "wednesday", "thursday", "friday", "saturday", "sunday".

 Output

Print "YES" (without quotes) if such situation is possible during some non-leap year. Otherwise, print "NO" (without quotes).

 Sample Input

monday
tuesday
sunday
sunday
saturday
tuesday

 Sample Output

NO
YES
YES

 Hint

In the second sample, one can consider February 1 and March 1 of year 2015. Both these days were Sundays.

In the third sample, one can consider July 1 and August 1 of year 2017. First of these two days is Saturday, while the second one is Tuesday.

 Problem Idea

解题思路:

【题意】

给你两个字符串a和b,分别表示一个星期中的某一天

问是否存在这么一种情况,一个非闰年中某个月的第一天是a,下个月的第一天是b

【类型】
签到题,取模
【分析】

因为是非闰年,一个月的天数只有三种情况:28、30、31

①对于只有28天的一个月,恰好是四周时间,显然该月第一天和下个月第一天是一个星期中的同一天

②对于有30天的一个月,四周多两天,故只要b比a多两天就可以了

③对于有31天的一个月，同理①和②

当然,一开始要先处理星期的问题,出题人比较人性化,给出了星期一到星期日的英文写法,不然英语水平不好的又得苦恼一会儿了

【时间复杂度&&优化】
O(1)

题目链接→Codeforces Problem 724A Checking the Calendar

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 100005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 20160519;
map<string,int> m;
string a,b;
int main()

    int k;
    m["monday"]=1;
    m["tuesday"]=2;
    m["wednesday"]=3;
    m["thursday"]=4;
    m["friday"]=5;
    m["saturday"]=6;
    m["sunday"]=7;//预处理
    cin>>a>>b;
    k=(m[b]-m[a]+7)%7;
    //printf("%d\\n",k);
    if(k==3||k==2||k==0)
        puts("YES");
    else
        puts("NO");
    return 0;

 Problem B-Batch Sort

Accept: 0    Submit: 0
Time Limit: 2 seconds    Memory Limit : 256 megabytes

 Problem Description

You are given a table consisting of n rows and m columns.

Numbers in each row form a permutation of integers from 1 to m.

You are allowed to pick two elements in one row and swap them, butno more than once for each row. Also, no more than once you are allowed to pick two columns and swap them. Thus, you are allowed to perform from 0 to n + 1 actions in total.Operations can be performed in any order.

You have to check whether it's possible to obtain the identity permutation 1, 2, ..., m in each row. In other words, check if one can perform some of the operation following the given rules and make each row sorted in increasing order.

 Input

The first line of the input contains two integers n and m (1 ≤ n, m ≤ 20) — the number of rows and the number of columns in the given table.

Each of next n lines contains m integers — elements of the table. It's guaranteed that numbers in each line form a permutation of integers from 1 to m.

 Output

If there is a way to obtain the identity permutation in each row by following the given rules, print "YES" (without quotes) in the only line of the output. Otherwise, print "NO" (without quotes).

 Sample Input

2 4
1 3 2 4
1 3 4 2
4 4
1 2 3 4
2 3 4 1
3 4 1 2
4 1 2 3
3 6
2 1 3 4 5 6
1 2 4 3 5 6
1 2 3 4 6 5

 Sample Output

YES
NO
YES

 Hint

In the first sample, one can act in the following way:

1.Swap second and third columns. Now the table is

1 2 3 4

1 4 3 2

2.In the second row, swap the second and the fourth elements. Now the table is

1 2 3 4

1 2 3 4

 Problem Idea

解题思路:

【题意】

给你一个n*m的矩阵

每行均是1~m的一个排列

现在规定:

①矩阵的每行最多只能交换一次某两个位置的数

②最多只能交换一次矩形某两列的数

问最终矩形的每一行的数是否都能够递增

【类型】
暴力
【分析】

如果此题没有交换某两列的这种操作,相信会简单得多

因为这样子的话我只要判断第i(1≤i≤n)行是不是最多只有两处s[i][j]!=j的位置就可以判定最终能否使得每一行的数都递增

但是,此题多了交换某两列的操作,当然,因为矩阵的规模比较小,做法还是比较简单的

首先二重循环暴力,交换第i列和第j列(1≤i<j≤m),然后再判断在交换第i列和第j列之后,是否每一行最多只有两处不符合递增的位置

需注意的是,不执行列交换的这种情况也要判一下

【时间复杂度&&优化】
O(N*M*M*M)

题目链接→Codeforces Problem 724B Batch Sort

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 25;
const int M = 100005;
const int inf = 1000000007;
const int mod = 20160519;
int n,m,s[N][N];
bool check()

    int i,j,k;
    for(i=1;i<=n;i++)
    
        for(k=0,j=1;j<=m;j++)
            if(s[i][j]!=j)
                k++;
        if(k>2)
            return false;
    
    return true;

int main()

    int i,j,k;
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
            scanf("%d",&s[i][j]);
    if(check())//不执行列交换的情况
    
        puts("YES");
        return 0;
    
    for(i=1;i<=m;i++)
        for(j=i+1;j<=m;j++)
        
            for(k=1;k<=n;k++)
                swap(s[k][i],s[k][j]);
            if(check())
            
                puts("YES");
                return 0;
            
            for(k=1;k<=n;k++)
                swap(s[k][i],s[k][j]);
        
    puts("NO");
    return 0;

 Problem C-Ray Tracing

Accept: 0    Submit: 0
Time Limit: 2 seconds    Memory Limit : 256 megabytes

 Problem Description

There are k sensors located in the rectangular room of size n × m meters. The i-th sensor is located at point (xi, yi). All sensors are located at distinct points strictly inside the rectangle.

Opposite corners of the room are located at points (0, 0) and (n, m). Walls of the room are parallel to coordinate axes.

At the moment 0, from the point (0, 0) the laser ray is released in the direction of point (1, 1). The ray travels with a speed of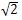meters per second. Thus, the ray will reach the point (1, 1) in exactly one second after the start.

When the ray meets the wall it's reflected by the rule that the angle of incidence is equal to the angle of reflection. If the ray reaches any of the four corners, it immediately stops.

For each sensor you have to determine the first moment of time when the ray will pass through the point where this sensor is located. If the ray will never pass through this point, print  - 1 for such sensors.

 Input

The first line of the input contains three integers n, m and k (2 ≤ n, m ≤ 100 000, 1 ≤ k ≤ 100 000) — lengths of the room's walls and the number of sensors.

Each of the following k lines contains two integers xi and yi (1 ≤ xi ≤ n - 1, 1 ≤ yi ≤ m - 1) — coordinates of the sensors. It's guaranteed that no two sensors are located at the same point.

 Output

Print k integers. The i-th of them should be equal to the number of seconds when the ray first passes through the point where the i-th sensor is located, or  - 1 if this will never happen.

 Sample Input

3 3 4
1 1
1 2
2 1
2 2
3 4 6
1 1
2 1
1 2
2 2
1 3
2 3
7 4 5
1 3
2 2
5 1
5 3
4 3

 Sample Output

1
-1
-1
2
1
-1
-1
2
5
-1
13
2
9
5
-1

 Hint

In the first sample, the ray will consequently pass through the points (0, 0), (1, 1), (2, 2), (3, 3). Thus, it will stop at the point (3, 3) after 3 seconds.

In the second sample, the ray will consequently pass through the following points: (0, 0), (1, 1), (2, 2), (3, 3), (2, 4), (1, 3), (0, 2), (1, 1), (2, 0), (3, 1), (2, 2), (1, 3), (0, 4). The ray will stop at the point (0, 4) after 12 seconds. It will reflect at the points (3, 3), (2, 4), (0, 2), (2, 0) and (3, 1).

 Problem Idea

解题思路:

【题意】

m*n的矩形内部有k个点,一条光线从(0,0)出发，向(1,1)方向以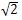米每秒运动

当光线碰到壁时会反射,碰到矩形的四个角时结束运动

问第一次经过那k个点的时间

若一个点不可达,则输出-1

【类型】
镜面反射,循环节
【分析】

刚开始拿到这道题,感觉除了暴力没其他想法,但是矩形规模有点大,暴力应该会超时,所以放弃暴力的想法

那我们尝试找找规律

当n=9,m=8时,光线的运动路线如下

当n=9,m=7时,光线的运动路线如下

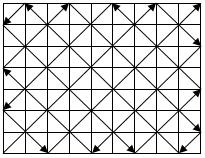
经过几种情况的尝试,也并没有发现有什么窍门

这时,需要从反射这个突破口下功夫

相信大家应该知道镜面反射中虚像的概念:

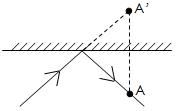
A'即为虚像

此题就可根据虚像的性质进行处理

以样例二为例(n=3,m=4)

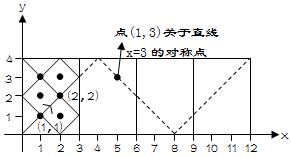
显然,对于点(x,y),关于右壁的对称点有两类:

①(x+2kn,y) k=0,1,2,…

②(2(k+1)n-x,y) k=0,1,2,…

而对称点还要判断是否出现在上升光线上 or 下降光线上

四种情况取时间最少的就是光线到达该点的时间

四种情况分别为:①x+2kn-y②x+2kn+y③2(k+1)n-x-y④2(k+1)n-x+y

那么如何判断点(x+2kn,y)在上升光线上呢?

当且仅当(x+2kn-y)%(2m)==0存在非负整数解时,在上升光线上

同理,当且仅当(x+2kn+y)%(2m)==0存在非负整数解时,在下降光线上

而要求第一次的时间,显然要求满足上式的最小k,那么我们可以通过预处理循环节(2kn)%(2m),以减小时间复杂度

这题的方法解释起来有点难,但理解了就会发现做法很简单

以上提供的是个人的一点看法,方便大家理解,如果还有不明白之处,欢迎提出,博主会尽快予以解答

【时间复杂度&&优化】
O(maxN,M,K)

题目链接→Codeforces Problem 724C Ray Tracing

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
//const int N = 100005;
//const int M = 26;
const __int64 inf = 1e18;
const int mod = 20160519;
int v[200010],N,M;
__int64 solve(int x,int y)

    int k=(M-(x-y+M)%M)%M;
    if(v[k]!=-1)
        return 1ll*v[k]*N+x;
    return inf;

int main()

    int n,m,k,p=0,current=0,i,x,y;
    __int64 ans;
    memset(v,-1,sizeof(v));
    scanf("%d%d%d",&n,&m,&k);
    N=2*n,M=2*m;
    while(v[current]==-1)//预处理循环节
    
        v[current]=p++;
        current=(current+N)%M;
    
    /*for(i=0;i<N;i++)
        printf("%d ",v[i]);
    puts("");*/
    for(i=0;i<k;i++)
    
        scanf("%d%d",&x,&y);
        ans=min(min(solve(x,M-y),solve(x,y)),min(solve(N-x,y),solve(N-x,M-y)));
        if(ans!=inf)
            printf("%I64d\\n",ans);
        else
            puts("-1");
    
    return 0;

 Problem D-Dense Subsequence

Accept: 0    Submit: 0
Time Limit: 2 seconds    Memory Limit : 256 megabytes

 Problem Description

You are given a string s, consisting of lowercase English letters, and the integer m.

One should choose some symbols from the given string so that any contiguous subsegment of length m has at least one selected symbol. Note that here we choose positions of symbols, not the symbols themselves.

Then one uses the chosen symbols to form a new string. All symbols from the chosen position should be used, but we are allowed to rearrange them in any order.

Formally, we choose a subsequence of indices . The selected sequence must meet the following condition: for every j such that 1 ≤ j ≤ |s| - m + 1, there must be at least one selected index that belongs to the segment [j,  j + m - 1], i.e. there should exist a k from 1 to t, such that j ≤ 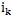 ≤ j + m - 1.

Then we take any permutation p of the selected indices and form a new string.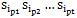

Find the lexicographically smallest string, that can be obtained using this procedure.

 Input

The first line of the input contains a single integer m (1 ≤ m ≤ 100 000).

The second line contains the string s consisting of lowercase English letters. It is guaranteed that this string is non-empty and its length doesn't exceed 100 000. It is also guaranteed that the number m doesn't exceed the length of the string s.

 Output

Print the single line containing the lexicographically smallest string, that can be obtained using the procedure described above.

 Sample Input

3
cbabc
2
abcab
3
bcabcbaccba

 Sample Output

a
aab
aaabb

 Hint

In the first sample, one can choose the subsequence 3 and form a string "a".

In the second sample, one can choose the subsequence 1, 2, 4 (symbols on this positions are 'a', 'b' and 'a') and rearrange the chosen symbols to form a string "aab".

 Problem Idea

解题思路:

【题意】

给你一个整数m和一个字符串s

现在你要从字符串s中选出一些字符

使得字符串s中任意长度为m的连续子序列都至少包含这些字符中的一个

要求选出的这些字符排列后字典序最小

【类型】
贪心+乱搞
【分析】

要使得选出的字符排列后字典序最小,有如下几个策略:

①假设最终选取的一系列字符中字典序最大的为x,那么字符串s中所有的y(字典序:y<x)都要选取

显然 字典序: aaabb < aabb

②在满足①的条件下,选取的字符x应尽可能少

显然 字典序: aaabb < aaabbb

【时间复杂度&&优化】
O(26×100000)

题目链接→Codeforces Problem 724D Dense Subsequence

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 100005;
const int M = 26;
const int inf = 1000000007;
const int mod = 20160519;
char s[N];
int m,v[M];
bool check(int k)//判断字符串s中任意长度为m的连续子序列是否至少包含所选字符中的一个

    int i,p;
    for(i=0;s[i]!='\\0'&&s[i]-'a'>k;i++);
    if(s[i]=='\\0'||i>=m)
        return false;
    for(p=i+m;s[i]!='\\0';i++)
    
        if(s[i]-'a'<=k)
            p=i+m;
        if(i>=p)
            break;
    
    if(s[i]=='\\0')
        return true;
    return false;

int main()

    int i,k,p,c=0,pos;
    scanf("%d",&m);
    scanf("%s",s);
    for(i=0;s[i]!='\\0';i++)
        v[s[i]-'a']++;
    for(i=0;i<26;i++)
    
        if(!v[i])
            continue;
        if(check(i))
            break;
        while(v[i]--)
            printf("%c",i+'a');
    
    //printf("%d\\n",i);
    //printf("%c\\n",i+'a');
    k=i;
    for(i=0;s[i]!='\\0'&&s[i]-'a'>=k;i++)
        if(s[i]-'a'==k&&i<m)
            pos=i;
    if(s[i]=='\\0'||i>=m)
        i=pos,c++,p=pos+m;
    else
        p=i+m;
    for(;s[i]!='\\0';i++)
    
        if(s[i]-'a'<k)
            p=i+m;
        if(s[i]-'a'==k)
            pos=i;
        if(i>=p)
            i=pos,c++,p=pos+m;
    
    while(c--)
        printf("%c",k+'a');
    puts("");
    return 0;

菜鸟成长记