HDU 5894 hannnnah_j’s Biologica(lucas定理求组合数+乘法逆元)——2016 ACM/ICPC Asia Regional Shenyang Online

Posted 2022-07-31 queuelovestack

此文章可以使用目录功能哟↑(点击上方[+])

 HDU 5894 hannnnah_j’s Biologica

Accept: 0    Submit: 0
Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)

 Problem Description

hannnnah_j is a teacher in WL High school who teaches biology.

One day, she wants to test m students, thus she arranges n different seats around a round table.

In order to prevent cheating, she thinks that there should be at least k empty seats between every two students.

hannnnah_j is poor at math, and she wants to know the sum of the solutions.So she turns to you for help.Can you help her? The answer maybe large, and you need to mod 1e9+7.

 Input

First line is an integer T(T≤1000).

The next T lines were given n, m, k, respectively.

0 < m < n < 1e6, 0 < k < 1000

 Output

For each test case the output is only one integer number ans in a line.

 Sample Input

2
4 2 6
5 2 1

 Sample Output

0
5

 Problem Idea

解题思路:

【题意】
n个位置围成环,m个人坐,要求相邻两个人之间必须至少隔k个位置

问有多少种坐法,结果对1e9+7取模

【类型】
lucas定理求组合数+乘法逆元
【分析】
其实此题可以这么理解

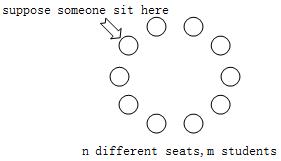
假定一个人已经坐在了某个位置,如图所示

那还剩下n-1个位置,而要求相邻两人之间必须隔k个位置,所以m个人就有m*k个位置不能坐

那剩下的位置数为n-1-m*k,由于一个人已经坐好,那我需要从这些剩下的位置中挑选出m-1个位置供剩下的m-1个人就坐

故组合数为C(n-m*k-1,m-1)

然后因为有n个位置,所以第一个人位置的选法就有n种

再考虑此题中每个人都是一样的,即不同方案仅仅是坐的位置序列不同,那上述做法会重复计算m次

比如有3个人,假设他们坐的位置是(2,4,7),那么,(4,2,7),(7,2,4)是重复计算的

故方案数的最终式子应为[C(n-m*k-1,m-1)*n/m]%1000000007

那求解组合数不用想肯定得用lucas定理,毕竟n和m有点大,直接打表已经存不下结果,且会超时

而除法取模部分,考虑到1000000007是质数,且m<1000000007,所以gcd(m,1000000007)=1,故可以直接采取乘法逆元

【时间复杂度&&优化】

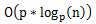
题目链接→HDU 5894 hannnnah_j’s Biologica

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 1000005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
__int64 fac[N];
void init()//预处理阶乘

    fac[0]=1;
    for(int i=1;i<=N;i++)
        fac[i]=i*fac[i-1]%mod;

__int64 pow_mod(__int64 a,__int64 b)

    __int64 s=1;
    a=a%mod;
    while(b)
    
        if(b&1)
            s=s*a%mod;
        a=a*a%mod;
        b>>=1;
    
    return s;

__int64 C(int n,int m)

    if(m>n)
        return 0;
    return  fac[n]*pow_mod(fac[m]*fac[n-m]%mod,mod-2)%mod;

__int64 Lucas(int n,int m)

    if(m==0)
        return 1;
    return C(n%mod,m%mod)*Lucas(n/mod,m/mod)%mod;

__int64 Quick_Mod(int a,int b)//快速幂

    __int64 res = 1,term = a % mod;
    while(b)
    
        if(b & 1) res = (res * term) % mod;
        term = (term * term) % mod;
        b >>= 1;
    
    return res;

int main()

    int t,n,m,k;
    init();
    scanf("%d",&t);
    while(t--)
    
        scanf("%d%d%d",&n,&m,&k);
        printf("%I64d\\n",((Lucas(n-m*k-1,m-1)*n)%mod)*Quick_Mod(m,mod-2)%mod);
    
    return 0;

菜鸟成长记