弗洛伊德的乌龟与兔子
Posted 却把清梅嗅
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了弗洛伊德的乌龟与兔子相关的知识,希望对你有一定的参考价值。

Floyd 判圈算法(Floyd Cycle Detection Algorithm),又称龟兔赛跑算法(Tortoise and Hare Algorithm),是一个可以在有限状态机、迭代函数或者链表上判断是否存在环,以及判断环的起点与长度的算法。
结论
- 1、如果链表上存在环,那么在某个环上以不同速度前进的2个指针必定会在某个时刻相遇;
- 2、根据结论1找到的相遇点可找到环的入口,初始化额外的两个指针:
ptr1,指向链表的头,ptr2指向相遇点。然后,每次将它们往前移动一步,直到它们相遇,它们相遇的点就是环的入口。
结论1是很显然的,结论2似乎有点匪夷所思,下面将针对以上结论分别进行证明。
证明
1.龟兔相遇
一个跑得快的人和一个跑得慢的人在一个圆形的赛道上赛跑,会发生什么?在某一个时刻,跑得快的人一定会从后面赶上跑得慢的人。
下图说明了这个算法的工作方式。
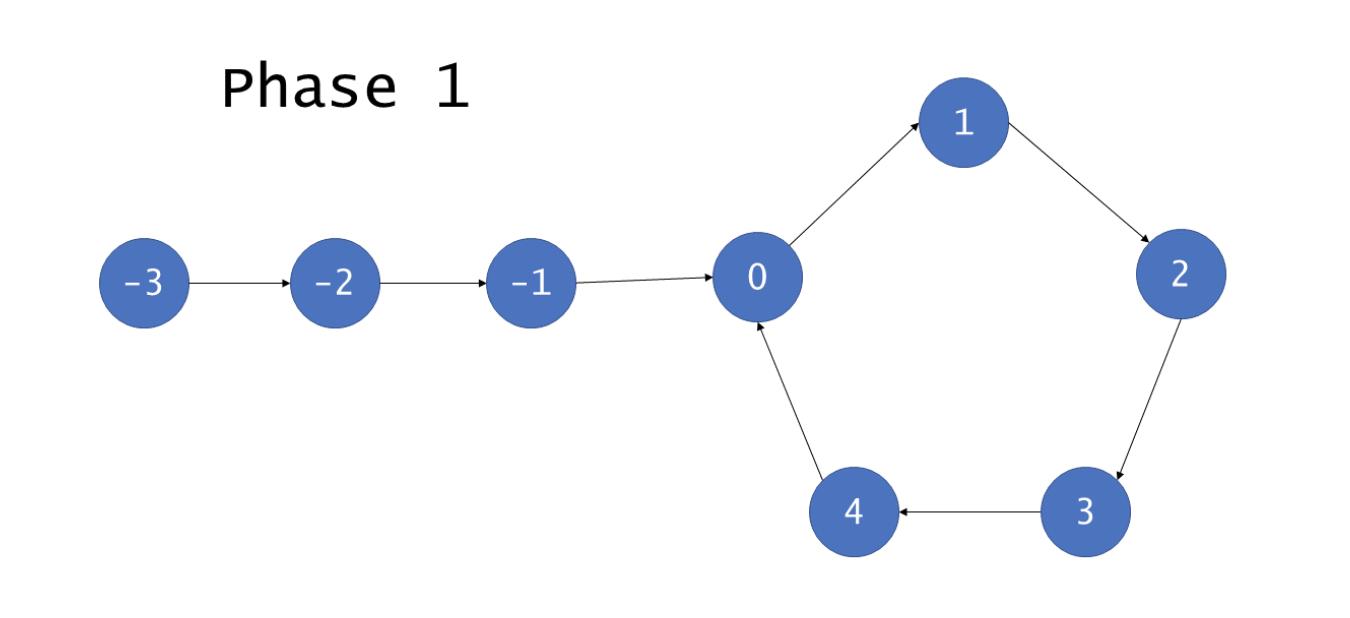
初始状态下,假设已知某个起点节点为节点F。现设两个指针 fast 和 slow,将它们均指向F。
同时让 fast 和 slow 往前推进,fast的速度为 slow 的2倍),直到 fast 无法前进,即到达某个没有后继的节点时,就可以确定从F出发不会遇到环。反之当 fast 和 slow 再次相遇时,就可以确定从F出发一定会进入某个环,设其为环C( fast 和 slow 推进的步数差是环长的倍数)。
2.计算环的入口
如何找到环的入口?
根据结论1找到的相遇点可找到环的入口,初始化额外的两个指针:
ptr1,指向链表的头,ptr2指向相遇点。然后,每次将它们往前移动一步,直到它们相遇,它们相遇的点就是环的入口。
下图对结论2进行证明。
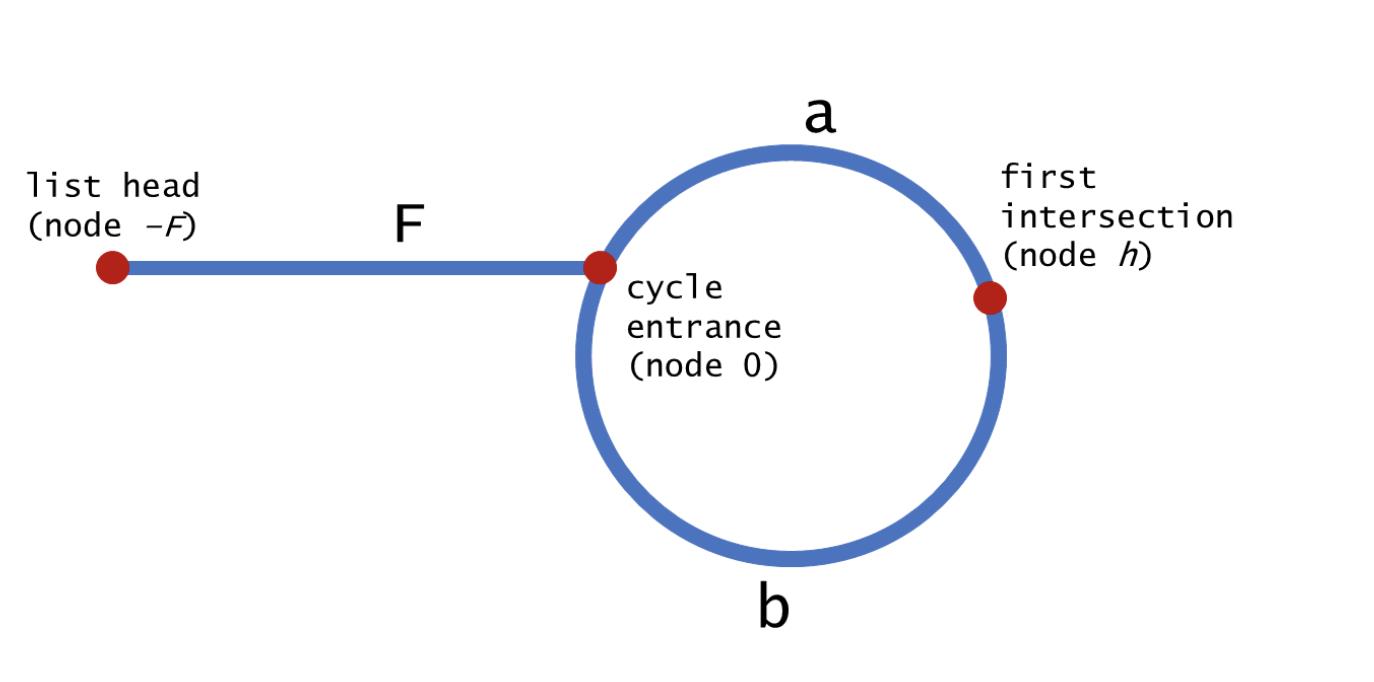
我们利用已知的条件:慢指针移动 1 步,快指针移动 2 步,来说明它们相遇在环的入口处:(下面证明中的 tortoise 表示慢指针,hare 表示快指针)
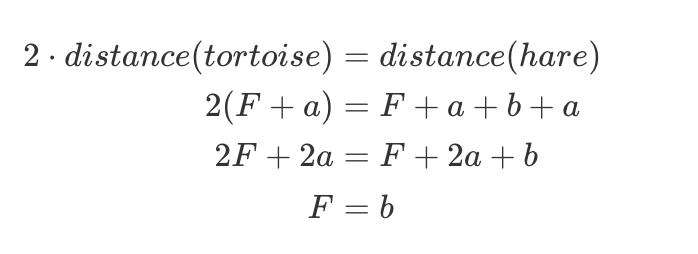
因为 F = b ,指针从 h 点出发和从链表的头出发,最后会遍历相同数目的节点后在环的入口处相遇。
算法描述
public class Solution
private ListNode getIntersect(ListNode head)
ListNode tortoise = head;
ListNode hare = head;
while (hare != null && hare.next != null)
tortoise = tortoise.next;
hare = hare.next.next;
if (tortoise == hare)
return tortoise;
return null;
public ListNode detectCycle(ListNode head)
if (head == null)
return null;
// 通过结论1,找到相遇点
ListNode intersect = getIntersect(head);
// 相遇点为空,则链表为非循环链表
if (intersect == null)
return null;
// 通过结论2,找到环的入口
// 分别定义两个指针,从head和相遇点开始前进,相遇点即为环的入口
ListNode ptr1 = head;
ListNode ptr2 = intersect;
while (ptr1 != ptr2)
ptr1 = ptr1.next;
ptr2 = ptr2.next;
return ptr1;
- 时间复杂度:
O(n) - 空间复杂度:
O(1)
例题
142. 环形链表 II
题目描述
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从0开始)。 如果 pos 是-1,则在该链表中没有环。
说明:不允许修改给定的链表。
- 难度:
Medium
解题思路
经典的 Floyd 算法的应用场景。
public class Solution
public ListNode detectCycle(ListNode head)
if (head == null || head.next == null) return null;
ListNode slow = head;
ListNode fast = head;
while (true)
if (fast == null || fast.next == null)
return null;
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break;
fast = head;
while (fast != slow)
fast = fast.next;
slow = slow.next;
return fast;
287. 寻找重复数 (Medium)
题目描述
给定一个包含 n + 1 个整数的数组 nums,其数字都在 1 到 n 之间( 包括 1 和 n ),可知至少存在一个重复的整数。假设只有一个重复的整数,找出这个重复的数。
- 示例 1:
输入: [1,3,4,2,2]
输出: 2
- 示例 2:
输入: [3,1,3,4,2]
输出: 3
- 难度:
Medium
解题思路
正常的思路是通过 HashSet , 或者通过排序以迅速找到重复数。
前者的时间和空间复杂度为 O(N),后者排序解决方案的时间复杂度为 O(NlogN) 空间复杂度为 O(1)。
可以取巧的是,这道题因为题目的关系,可以将题目中数组视为 索引 与 对应值 的关系视为一个 链表,因为重复数的关系,它还是一个 循环链表,因此依然可以通过 Floyd 算法解决:
class Solution
public int findDuplicate(int[] nums)
int fast = nums[0];
int slow = nums[0];
// 找到相遇节点
while (true)
slow = nums[slow];
fast = nums[nums[fast]];
if (slow == fast)
// 找到重复数
int ptr1 = nums[0];
int ptr2 = fast;
while (ptr1 != ptr2)
ptr1 = nums[ptr1];
ptr2 = nums[ptr2];
return ptr1;
参考&感谢
关于我
Hello,我是 却把清梅嗅 ,如果您觉得文章对您有价值,欢迎 ❤️,也欢迎关注我的 博客 或者 Github。
如果您觉得文章还差了那么点东西,也请通过关注督促我写出更好的文章——万一哪天我进步了呢?
以上是关于弗洛伊德的乌龟与兔子的主要内容,如果未能解决你的问题,请参考以下文章