第二节：层次聚类算法之BIRCH算法

Posted 快乐江湖

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了第二节：层次聚类算法之BIRCH算法相关的知识，希望对你有一定的参考价值。

文章目录

一：BIRCH算法概述

BIRCH算法：该算法于1996年提出，尤其适用于大型数据库。它会增量地对输入数据进行聚类，有时甚至只需对所有数据扫描一遍就可以产生结果，当然额外的扫描肯定可以提升聚类效果，而且还可以有效处理噪声。BIRCH算法需要引入以下两个概念

  • 聚类特征（CF）
  • 聚类特征数（CF树）

聚类特征数类似于平衡B+树，CF树的每个结点是由若干聚类特征CF组成的

（1）聚类特征CF

聚类特征CF：一个聚类特征由一个三元组表示，它给出了一个簇的汇总描述。在大小为 N N N的 d d d维数据集 x 1 , x 2 , . . . , x N \\x_1,x_2,...,x_N\\ x1​,x2​,...,xN​上，定义聚类特征如下

C F = ( N , L S ⃗ , S S ) CF=(N,\\vecLS,SS) CF=(N,LS ,SS)

  • N N N：数据数量
  • L S ⃗ \\vecLS LS ： N N N个数据点的线性和，也即 ∑ i = 1 N x i ⃗ \\sum\\limits_i=1^N \\vecx_i i=1∑N​xi​ ​
  • S S SS SS： N N N个数据点的平方和，也即 ∑ i = 1 N x i 2 ⃗ \\sum\\limits_i=1^N \\vecx_i^2 i=1∑N​xi2​ ​

聚类特征是可以求和的

  • C F 1 = ( N 1 , L S 1 ⃗ , S S 1 ) CF_1=(N_1,\\vecLS_1,SS_1) CF1​=(N1​,LS1​ ​,SS1​)
  • C F 2 = ( N 2 , L S 2 ⃗ , S S 2 ) CF_2=(N_2,\\vecLS_2,SS_2) CF2​=(N2​,LS2​ ​,SS2​)
  • C F 1 + C F 2 = ( N 1 + N 2 , L S 1 ⃗ + L S 2 ⃗ , S S 1 + S S 2 ) CF_1+CF_2=(N_1+N_2,\\vecLS_1+\\vecLS_2,SS_1+SS_2) CF1​+CF2​=(N1​+N2​,LS1​ ​+LS2​ ​,SS1​+SS2​)

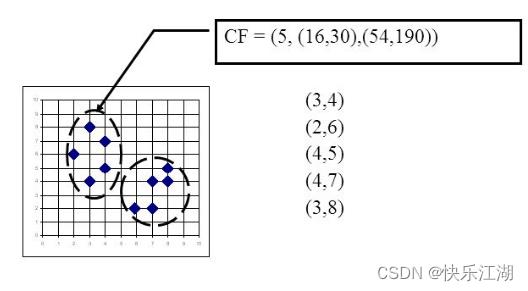
如下图，有5个样本形成的一个簇，分别是 ( 3 , 4 ) , ( 2 , 6 ) , ( 4 , 5 ) , ( 4 , 7 ) , ( 3 , 8 ) (3, 4),(2,6),(4,5),(4,7),(3,8) (3,4),(2,6),(4,5),(4,7),(3,8)，则有

  • N N N：5
  • L S ⃗ \\vecLS LS ： ( 3 + 2 + 4 + 4 + 3 , 4 + 6 + 5 + 7 + 8 ) = ( 16 , 30 ) (3+2+4+4+3, 4+6+5+7+8)=(16, 30) (3+2+4+4+3,4+6+5+7+8)=(16,30)
  • S S SS SS： ( 3 2 + 2 2 + 4 2 + 4 2 + 3 2 + 4 2 + 6 2 + 5 2 + 7 2 + 8 2 ) = 244 (3^2+2^2+4^2+4^2+3^2 +4^2+6^2+5^2+7^2+8^2)=244 (32+22+42+42+32+42+62+52+72+82)=244

（2）聚类特征树

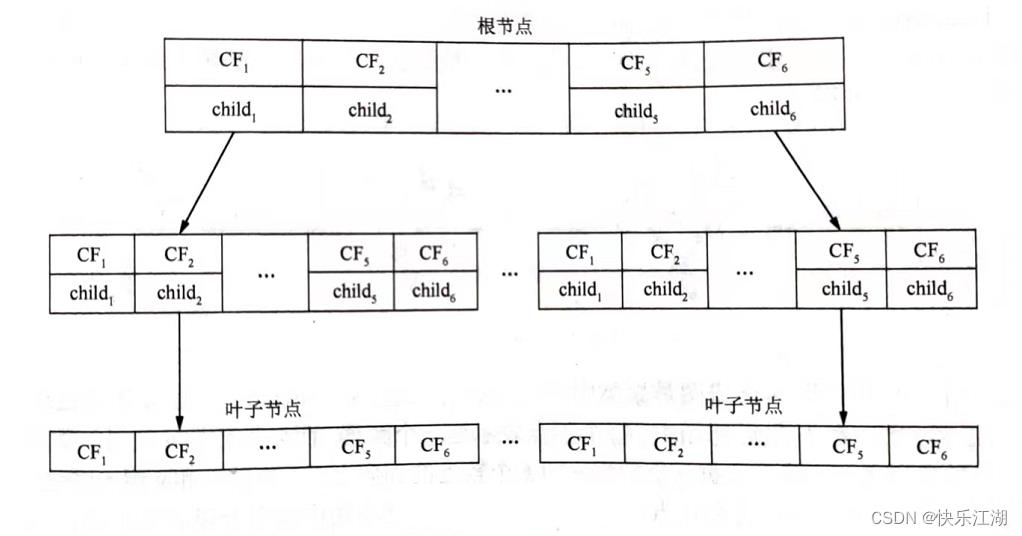
聚类特征树：一个CF树存储了层次聚类的聚类特征。它存储了层次聚类的聚类特征。下图是一个典型的CF树。CF树中每个非叶结点存储的CF是其孩子结点的CF总和，也即父结点存储的信息是其子结点存储信息的汇总。一个叶子结点至多包含 L L L个条目，每个条目是一个聚类特征三元组，每个叶子结点有两个指针，即prev和next，用来把所有的叶子结点连接起来

一个CF树有如下两个参数，当阈值 T T T越大时树就会越小，它们决定了树的大小

  • 分支因子 B B B：表示每个非叶结点最大的孩子数目
  • 阈值 T T T：：表示存储在树的叶子结点中的子聚类的最大半径

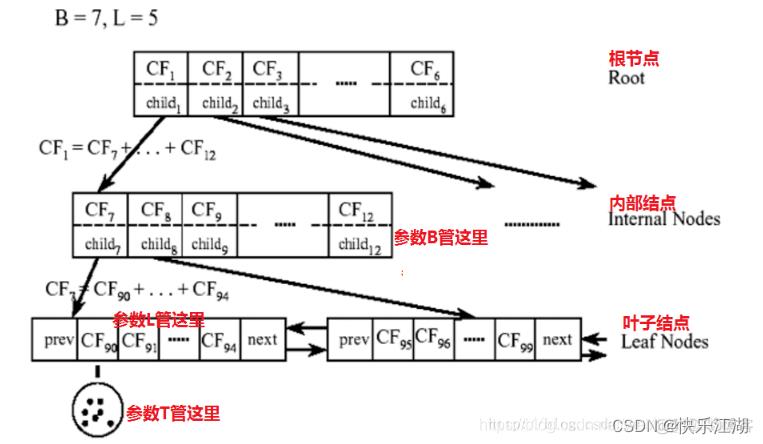
如下图，在CF树中，对于父结点的每个CF结点，它的 ( N , L S ⃗ , S S ) (N,\\vecLS,SS) (N,LS ,SS)三元组的值等于这个CF结点所指向的所有子结点的三元组之和

（3）聚类特征树的生成

A：生成规则

聚类特征树的生成规则：CF树是随数据的输入动态增长的，生成CF树的步骤如下