零知识谜题

Posted 2022-07-20 sCrypt 智能合约

这是我们与 nChain 合作的第三部分。我们要特别感谢 Enrique Larraia 博士撰写本文所依据的白皮书并帮助指导实施。

一个标准的支付交易可以看作是一个公钥迷题。如果他知道给定地址/公钥的相应私钥，他就可以花费硬币。与会透露原像的哈希谜题不同，公钥谜题的解决方案，即私钥，永远不会被透露。这是使用数字签名实现的，这是一种零知识证明：一个人在不公开私钥的情况下证明私钥的知识。

我们使用标准的零知识证明技术来概括私钥的知识证明。因此，我们可以构建任意复杂的谜题，称为零知识 (ZK) 谜题，作为支出条件。一些用例包括：

• 支付给椭圆曲线上的公钥，该椭圆曲线不同于当今比特币中使用的曲线 secp256k1

• 支付给一组公钥，如果一个人知道任何一个公钥的私钥，就可以花费这些硬币，而无需透露是哪一个。

∑ 协议

∑-协议是一种零知识协议，用于在不公开值本身的情况下证明知道某种关系中的值。例如，证明知道离散对数，即给定 g 和 y，证明知道 x 满足 gˣ = y 的而不揭示 x。它由证明者 Peggy 和验证者 Victor 之间的三个步骤组成，称为承诺、挑战和响应，如下图所示（名称 ∑ 来源于形状）。

图 1：∑ 协议

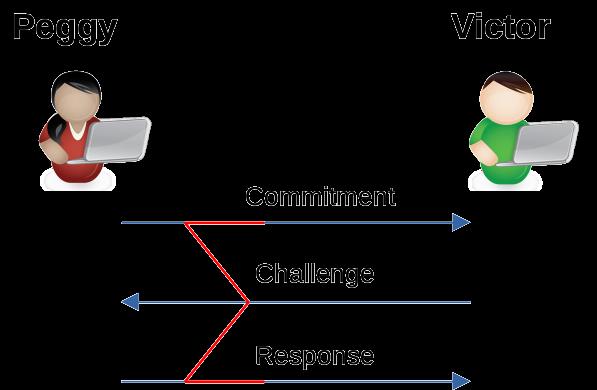
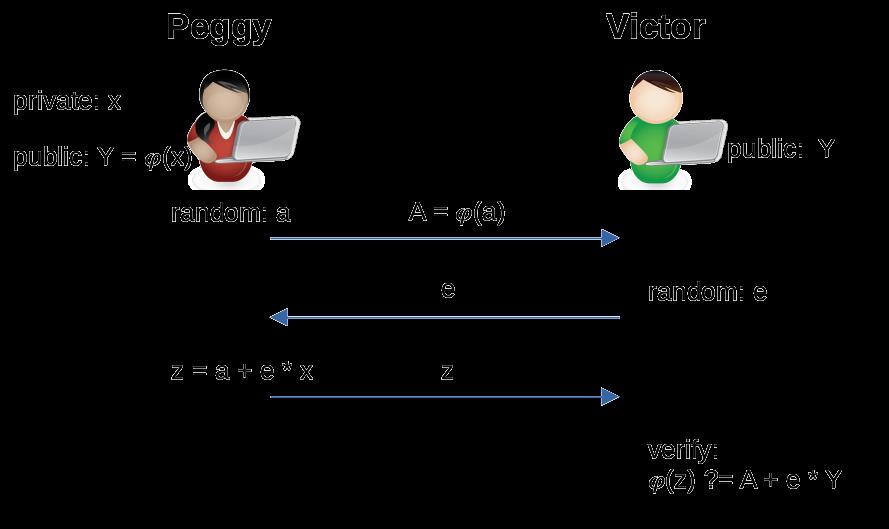
例如，Peggy 想要让 Victor 相信她知道 Y = 𝜑(x) 中的 x 而不透露 x，其中 𝜑 是一个函数¹。双方都接收 Y 作为输入。

1. Peggy 使用随机数 a 计算承诺 A。她与 Victor 共享 A，但没有透露 a。
2. Victor 生成一个随机数 e 作为挑战并与 Peggy 共享。
3. Peggy 使用 a 和 e 计算答案 z 并返​​回给 Victor。

通过检查公共信息 A、Y、z 和 e，Victor 判断 Peggy 知道 x 是否等式成立。

图 2：在 𝜑 下证明知道 x 的 ∑ 协议

Fiat-Shamir 启发式

上面的 ∑ 协议需要 Peggy 和 Victor 之间的交互。我们可以使用标准的 Fiat-Shamir启发式 技术来消除交互。基本思想是使用像 sha256 这样的加密哈希函数 H 来模拟 Victor 的挑战 e。通过散列 Y 和 A，特定于协议执行，e 可以被视为随机²。证明知道 x 的新 ∑ 协议变为：

图 3：在 𝜑 下证明知道 x 的 非交互式 ∑ 协议

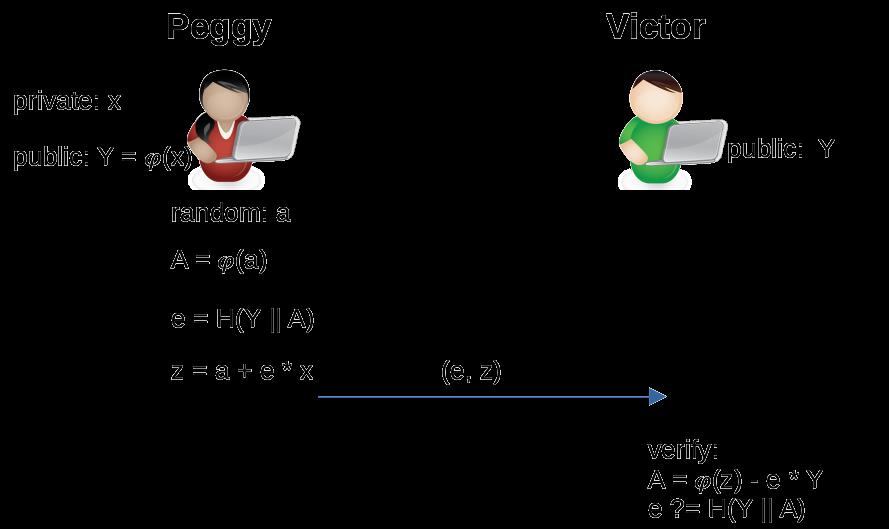
只有一步：Peggy 将证明 (e, z) 发送给 Victor。Victor 使用图 2 中的等式推导出 A 并检查 e == H(Y || A) 是否成立。

零知识谜题示例

我们将非交互式 ∑ 协议应用于比特币，其中 𝜑(x) = x * G，G 是生成点。

支付到通用公钥 (P2GPK)

我们使用∑协议，用证明 (e，z) 替换签名。它是标准 Pay to Public Key (P2PK) 谜题的扩展。
以下代码实现了验证，使用了我们的椭圆曲线库。

// pay to a generic public key
contract P2GPK 
    // public key
    Point pk;

    public function unlock(int e, int z, SigHashPreimage preimage) 
        require(Tx.checkPreimage(preimage));

        // Compute A = z * G - e * PK
        Point zG = EC.multByScalar(EC.G, z);
        Point ePK = EC.multByScalar(this.pk, e);
        Point A = EC.addPoints(zG, EC.negatePoint(ePK));

        // Compute e = H(preimage || PK || A)
        bytes pk_ = EC.point2PubKey(this.pk);
        bytes A_ = EC.point2PubKey(A);
        int e_ = Utils.fromLEUnsigned(sha256(preimage + pk_ + A_));

        require(e == e_);
    

P2GPK 合约

它与图 3 中的验证相同，只是我们还在 H 中添加了 sighash 原像，就像比特币签名当前所做的那样。否则，攻击者可以更改交易并将硬币重定向到他的地址，因为证明在解锁脚本中是公开的，即上述函数 unlock() 的参数。H 在第 17 行被执行 SHA256运算。

与内置签名检查相比，P2GPK 享有多项优势。

• 它可以使用比硬编码曲线 secp256k1 具有更高安全性的曲线，例如 secp521r1。如果数十年来大量比特币由一个密钥控制，这可能是可取的。这也意味着通过使用现有的操作码³，比特币可以升级到更安全的签名方案，而不会破坏更改协议。

• 它可以重用其他地方的兼容密钥。例如，PGP 支持椭圆曲线密钥，比特币可以发送到 PGP 密钥，即使它们基于其他曲线。

总结

到目前为止，我们只将 ∑ 协议应用于单个谜题。∑ 协议是模块化的，并且可以通过使用例如逻辑串联/与 和并联/或 组合在一起。因此，我们可以构建更高级的谜题，例如：

支付到群组密码（P2GP）：任何知道任意群组密码的人都可以通过提供证明来花费资金，而无需透露使用了哪一个群组密码。这是 1-of-n 多重签名的概括，但更私密。例如，Peggy 证明她知道公钥 Y 或 Z 的私钥，即她知道 x 使得：

x * G == Y || x * G == Z

支付到阈值群组密码（P2TGP）:使用 AND 和 OR 组合的证明，一个组中的 n 个成员中的任何 m 个可以集体赎回 UTXO，而无需透露是哪些 m 个成员。这包括了 P2GP 和 m-of-n 多重签名。例如，一个 2-of-3 零知识谜题需要：

x * G == X && y* G == Y || x * G == X && z * G == Z || y * G == Y && z * G == Z

致谢

这是与 nChain 在 1617 号白皮书上的合作：Enrique Larraia 博士的零知识迷题。

---

[1] 𝜑 必须是单向群同态，例如离散对数。

[2] 假设 H 是一个随机预言机。

[3] sha256、ripemd160等哈希函数可以被升级。