第一节：层次聚类算法概述聚合和分裂方法

Posted 2022-07-18 快乐江湖

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了第一节：层次聚类算法概述聚合和分裂方法相关的知识，希望对你有一定的参考价值。

文章目录

一：层次聚类算法概述
二：聚合方法
三：分裂方法

一：层次聚类算法概述

（1）层次聚类

层次聚类：层次聚类算法的出现是为了解决基于划分聚类算法中存在的一些缺陷，主要有

基于划分的聚类算法十分依赖于超参数 $k$ ，并且在很多情况下 $k$ 是无法确定的
基于划分的聚类算法存在初始化的问题，不良的初始化会导致聚类效果低下

层次聚类算法有两种思路，分别是分裂层次聚类算法（DHC）和聚合层次聚类算法（AHC）

分裂层次聚类算法（DHC）：先将所有数据视为一个类，然后基于某种准则在已有类中选择一个类将其分割为两个类，重复分割以达到最终聚类目的
聚合层次聚类算法（AHC）：先将每个数据视为单独的类，然后按某种距离度量方法选择距离最近的两个或者多个类进行合并，重复合并直到最后剩下一个类

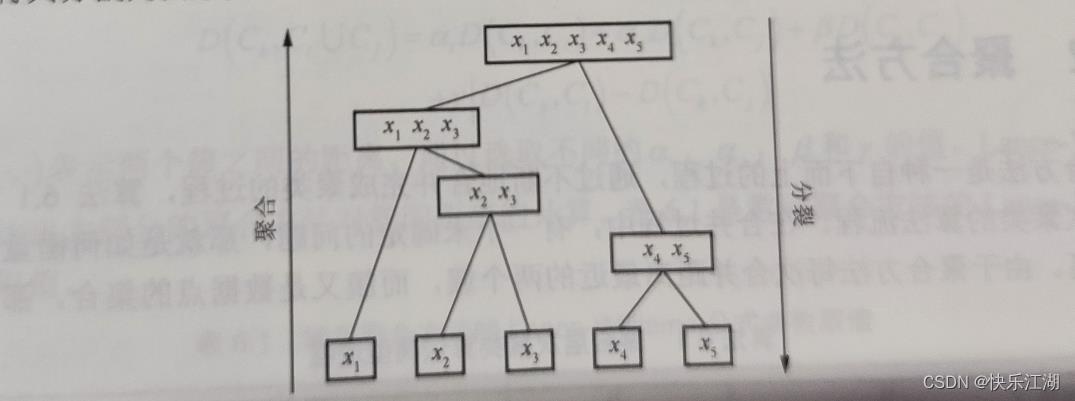
其中，聚合层次聚类算法（AHC）较分裂层次聚类算法（DHC）更多一点，，主要是因为分裂层次聚类算法（DHC）理论复杂度高

（2）聚合和分裂各自研究的重点

聚合层次聚类算法（AHC）：重点研究的是如何衡量两个簇之间的距离。也即，如何在已知集合内元素间距离的情况，计算两个集合之间的距离。例如

Single-link方法：采用两个簇之间距离最短的数据对间距离作为两个簇的距离
Complete-link方法：采用两个簇之间距离最远的数据对间距离作为两个簇的距离

分裂层次聚类算法（DHC）：有如下两个重点研究问题

如何选择下一步要分裂的簇：例如DIANA算法建议选择直径最大的簇、DISMEA算法选择平方距离最大的簇
如何将一个簇中的顶点划分到两个集合中，从而生成两个簇：例如DIANA算法通过定义一个函数来判断并决定簇的分割、DISMEA算法则直接使用 $k$ -均值算法来分割簇

（3）优缺点

优点：

（相较于基于划分的聚类算法）可以实现聚类过程与参数无关以及更加灵活的目的
给出了数据聚类过程中更加全面丰富的描述
层次聚类可以表示为层次图，在层次图中可以看到任意两个样本合并到一个簇中的过程

缺点：

时间复杂度过高，大多都在 $O(n^2)$ 级别
算法没有“回头路”，如果聚类过程中某一步的合并或者分裂是错误的，那么在后续步骤中是没有办法修正的

二：聚合方法

聚合方法：前面说过，这是一个自下而上的过程，通过不断合并完成以完成聚类。在合并过程中最大的问题就是如何衡量两个簇之间的距离，由于聚合方法每次合并距离最近的两个簇，而簇又是数据点的集合，那么问题最后就变成了如何通过簇中的数据点来衡量簇与簇之间的距离。这个问题促成了很多聚合方法的产生，下图展示了两类聚合方法

图方法：一个类可以通过子图或者数据点来表达
几何方法：一个类通过一个原本不存在的中心点来表达

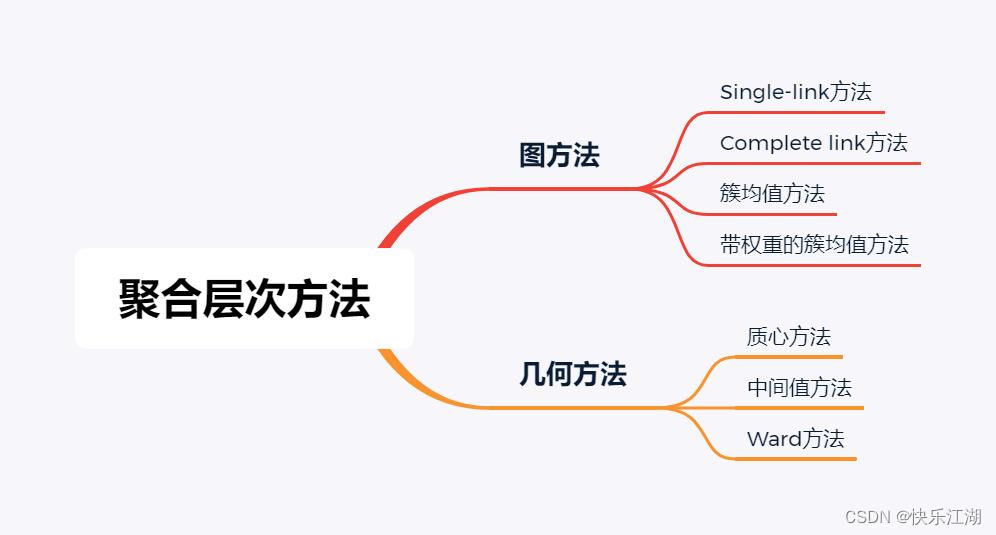
尽管聚合方法有很多种，但所有方法的目标都是计算两个簇之间的距离。Lance-Williams公式将上述方法中涉及的公式做了统一，用于计算两个簇合并后与其他簇之间的距离，如下

$D(C_k,C_i \\cup C_j)=\\alpha_i D(C_k,C_i)+\\alpha_j D(C_k,C_j )+\\beta D(C_i,C_j)+\\gamma|D(C_k,C_i) -D(C_k,C_j)|$

$D (,)$ 表示两个簇之间的距离

通过选取不同的 $\\alpha_i$ , $\\alpha_j$ , $\\beta$ 和 $\\gamma$ ，Lance-Williams公式可以表达出大部分的聚合方法对簇间距离的计算，如下表

	$\\alpha_i$	$\\alpha_j$	$\\beta$	$\\gamma$
Single-link方法	$\\frac12$	$\\frac12$	0	- $\\frac12$
Complete-link方法	$\\frac12$	$\\frac12$	0	$\\frac12$
簇均值方法	$\\fracn_in_i+nj$	$\\fracn_jn_i+nj$	0	0
带权重簇均值方法	$\\frac12$	$\\frac12$	0	0
质心方法	$\\fracn_in_i+nj$	$\\fracn_jn_i+nj$	- $\\fracn_in_j(n_i+nj)^2$	0
中间值方法	$\\frac12$	$\\frac12$	- $\\frac14$	0
Ward方法	$\\fracn_i+n_j\\sum ijk$