HashMap源码解读(中篇)
Posted Killing Vibe
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了HashMap源码解读(中篇)相关的知识,希望对你有一定的参考价值。
文章目录
前言
上一篇博主写了一些关于HashMap的前置知识,简单易懂:
下面将深入HashMap源码,进行解读。
看源码不是盲目看书,要有的放矢,带着疑问去看。
本文章将围绕这几个疑问展开:
- HashMap的哈希函数是如何设计的?
- put方法的逻辑是什么?到底是如何存储元素的?
- 当发生冲突时,是如何解决的?
- 哈希表冲突比较严重时,如何扩容resize?
一、进入JDK中的源码(InteliJ IDEA为例)
有两种快捷方式:
-
双击shift,输入HashMap类名即可。

-
直接在使用的类上,ctrl+鼠标左键点进去即可
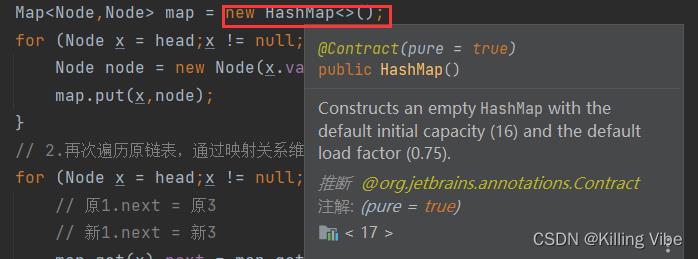
二、HashMap的结构
JDK8之后HashMap的结构图如下:(可先看下面再回来看这个结构图)
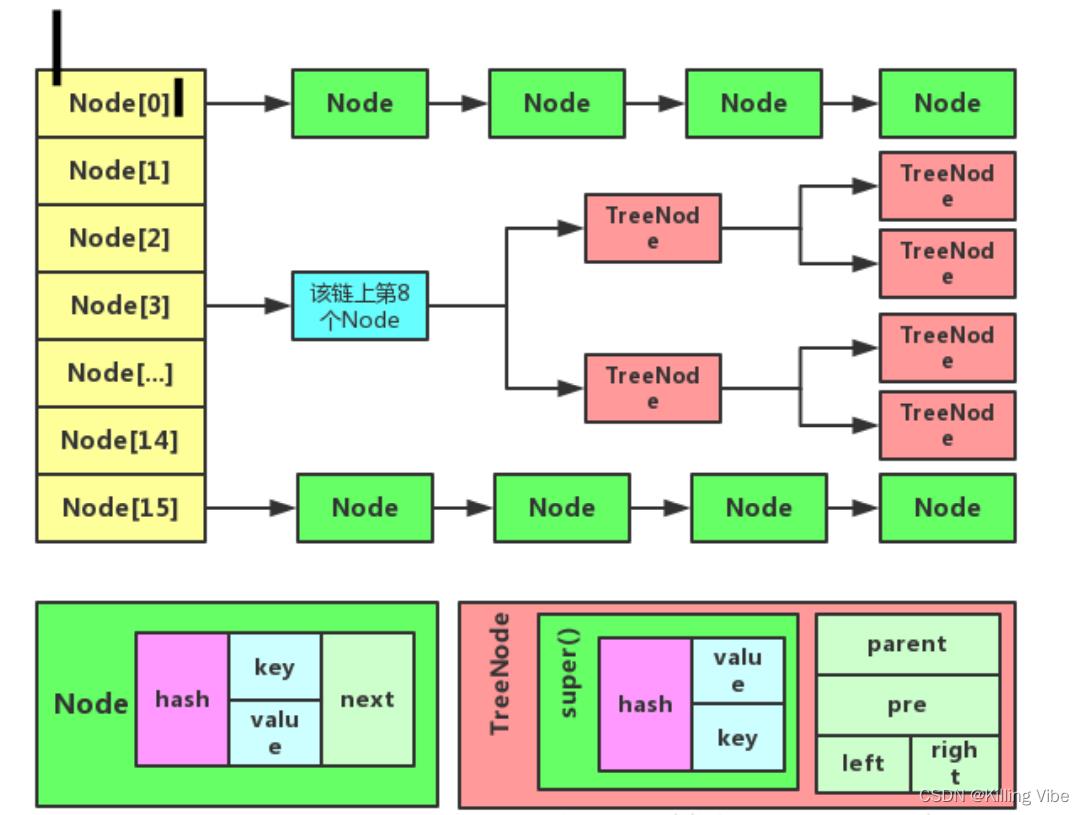
JDK8之前的HashMap就是数组+链表,JDK8之后采用数组+链表+红黑树
冲突严重的链表会被“树化”,将链表转为红黑树,提高冲突严重的链表的查询效率。
三、源码解读
3.1 属性解读
如图所示:
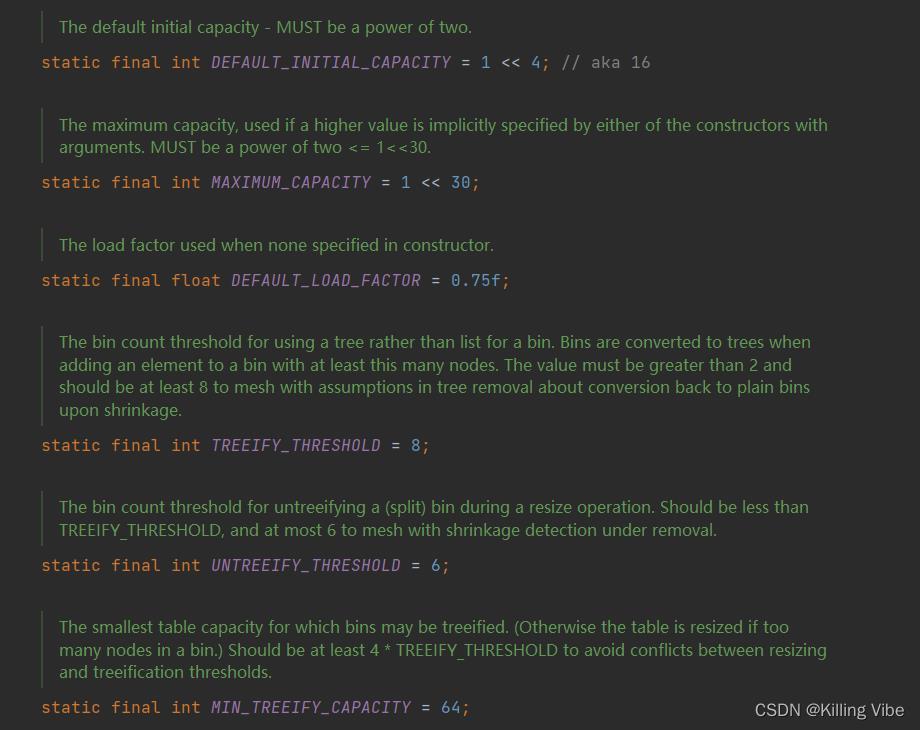
图中有六条属性,下面逐一解释:
1. static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
默认初始化的数组大小 (默认的哈希桶数量) : 16
注:哈希桶就是哈希表中一个个的数组元素,不包括链表元素
2.static final int MAXIMUM_CAPACITY = 1 << 30;
最大的数组容量:
2
30
2^30
230
3.static final float DEFAULT_LOAD_FACTOR = 0.75f;
默认负载因子,默认时开始保存的元素个数最多为 16 * loadFactor = 12 个
4.static final int TREEIFY_THRESHOLD = 8;
树化阈值。某个哈希桶中的链表长度超过8才会触发“树化”操作
5.static final int UNTREEIFY_THRESHOLD = 6;
“解树化” 当某个哈希桶中的红黑树结点个数过小,< = 6时,就会将红黑树还原为链表。
6.static final int MIN_TREEIFY_CAPACITY = 64;
树化有两个条件:
- 此时哈希表的哈希桶个数 >= 64
- 单个链表的结点个数 >= 8
若某个链表长度 >= 8 ,但此时哈希桶的数量不足64,则只是简单的哈希表扩容而已。
3.2 put方法解读
如图所示:

内部存储调用的是putVal方法,方法里面参数主要是hash值和key,value值。
3.2.1 HashMap中的hash方法
源码如下:
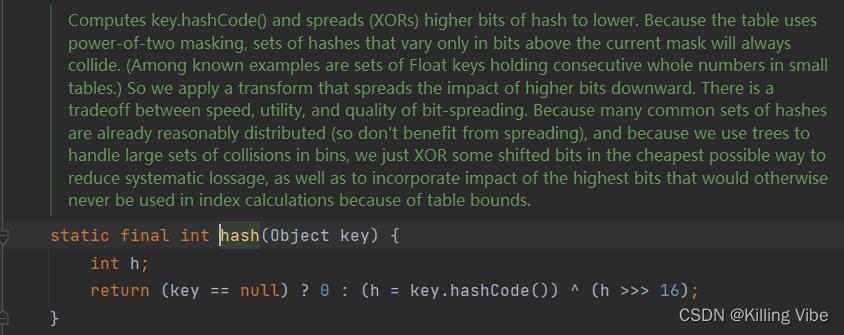
1.首先判断传入的Key值是否为null? 如果为null,直接放入数组索引为0的哈希桶中。
2.如果传入的Key值不为null,则将key的hashCode 无符号右移16位,保留高16位 然后和 原hashCode作 异或运算,求得数组索引。
注意:Key对象所在类的hashCode方法若没有覆写,则默认调用Object提供的hashCode方法。
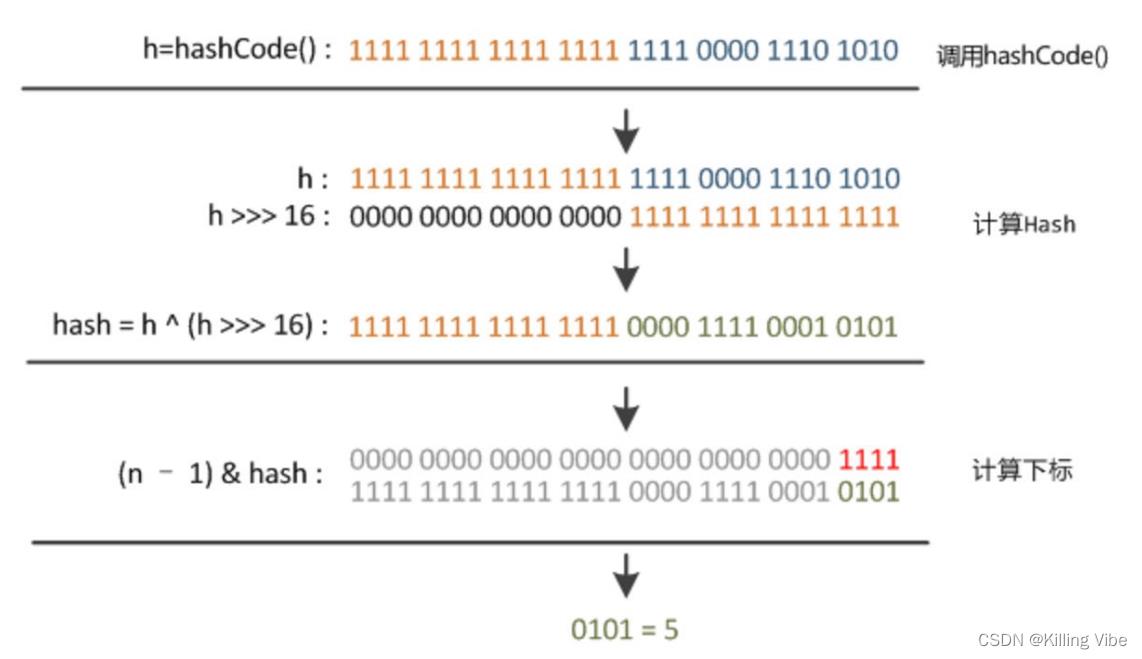
- 高低16位都参与哈希函数的运算,尽可能保证不同key映射到比较均衡的状态。
- 原32位的hashCode和只保留高16的数字做异或运算
- 高低位树都参与hash运算得到的值更加平均
- 哈希函数设计理念:经过hash运算得到的值尽可能地平均
此时求出地hash值还不是当前数组的索引,只是经过hash运算得到的一个比较均衡的值,hash值还要经过如下红框的位运算,得到数组索引值:

上一步得到的key的hash值和当前哈希表的长度-1 进行 & 运算就可以得到索引值。(位运算的效率是最高的)
- 相当于hash % 数组长度取模(n)
- 前提是n必须为 2^n (初始化的哈希桶数量必须为2 ^ n)。
- 将任意的正整数转为哈希桶数量之内的小整数 => i 就是当前key求的哈希桶的编号
3.2.2 HashMap中的putVal方法
JDK中源码如下
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict)
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else
for (int binCount = 0; ; ++binCount)
if ((e = p.next) == null)
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
if (e != null) // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
代码解读:
1.首先判断当前哈希表是否为空,若为空,进行默认初始化操作(resize()函数里面包括了扩容、数据搬移和初始化操作)
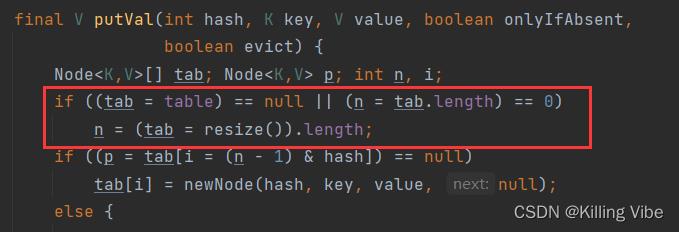
2.tab[i] = 这个哈希桶的头结点元素,当这个键值对计算出的哈希桶链表为空,直接将当前新元素放入链表的头部。
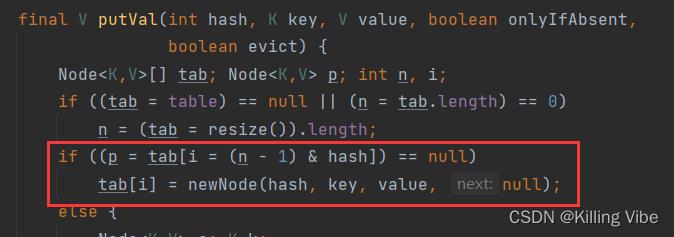
- 此时哈希表不为空且对应链表头部已经有元素了

4.链表不为空但是链表的头部元素key和新键值对的key相同(equals相同),hash值也相同,认为是同一个元素,替换头结点。

5.此时这个哈希桶对应的链表已经树化,调用RB的逻辑进行红黑树上的结点插入处理。
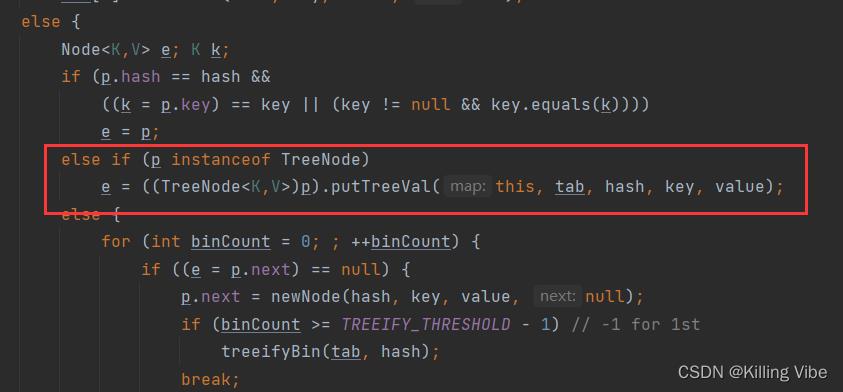
6. 链表的插入逻辑,新节点尾插入链表尾部,如果此时链表长度大于树化阈值,则执行treeifyBin()树化处理,注意此时哈希桶对应的还是链表,若哈希桶数量小于64,只是扩容,并不树化。

treeifyBin函数:若哈希桶数量小于64,只是扩容,并不树化。

7.新插入的元素的Key已经存在了,只是更新Value值即可。

8.判断添加元素之后整个的哈希表大小是否超过threshold,若超过则执行resize()扩容
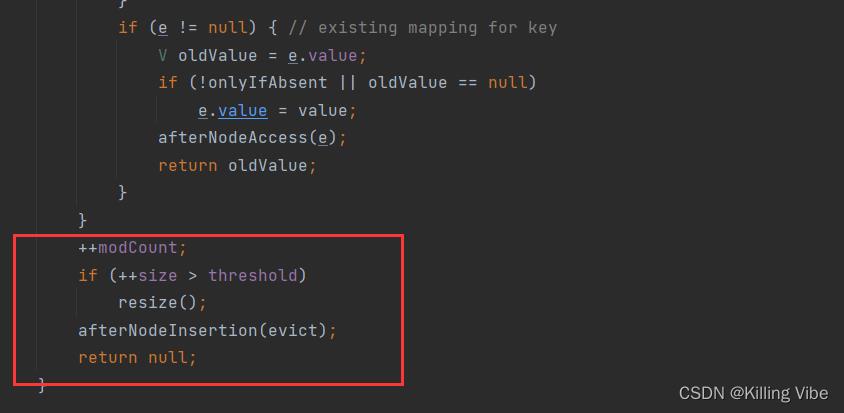
未完待续
本文解读了HashMap中的属性 以及 Put方法 ,对hashCode和equals 方法进行了一个扩展,以及对HashMap的Key唯一性进行了解释,后篇文章博主将会更新resize方法的解读以及 HashMap的构造方法懒加载等,感谢各位继续关注博主更新~~😀
HashMap 源码解读
HashMap 源码解读
在很多面试中,都会涉及到HashMap的问题,比如说问你HashMap存储结构,get、put的时间复杂度,或者扩容机制等等,这次我们来通过对源码的阅读,来实现对HashMap的理解!(大量源码源码警告!!!)
先看类的继承结构:
public class HashMap<K,V> extends AbstractMap<K,V>
implements Map<K,V>, Cloneable, Serializable {
...
}
可以看到HashMap继承了抽象类AbstractMap,实现了Map、Cloneable、Serializable接口。
这边有点奇怪,明明抽象类AbstractMap已经实现了Map接口,为什么HashMap又要实现一下?可能的原因:1、为了使用getInterfaces可以获取到Map,因为这样子没法获取到父类的接口;2、笔误(据说是作者 Jpsh Bloch自己说的。。。)
对于这些接口中的方法就不单独解释了,下面一起来看源码就好。
首先是一些常量属性:
// 默认初始化容量,16。必须是 2 的幂次。
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
// 最大容量 2^30,在构造函数中可以设置,必须是 2 的幂次。
static final int MAXIMUM_CAPACITY = 1 << 30;
// 默认装载因子 0.75,构造函数中可以自己设置
static final float DEFAULT_LOAD_FACTOR = 0.75f;
// 变成红黑树结构的容量,大于等于 8 就从表结构变成了红黑树结构
static final int TREEIFY_THRESHOLD = 8;
// 变成表结构的容量,小于等于 6 就从红黑树结构变成了表结构
static final int UNTREEIFY_THRESHOLD = 6;
// 红黑树结构的最小容量,最少是 4 * TREEIFY_THRESHOLD 以避免重构时的冲突
static final int MIN_TREEIFY_CAPACITY = 64;
然后是一个静态内部类Node<K,V>:
// 实现了 Entry 接口可用于 AbstractMap 中的方法
static class Node<K,V> implements Map.Entry<K,V> {
// hash 值
final int hash;
// 键
final K key;
// 值
V value;
// 下一个节点
Node<K,V> next;
Node(int hash, K key, V value, Node<K,V> next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
// Node 的 get、set 方法,用于被外部类方法调用
public final K getKey() { return key; }
public final V getValue() { return value; }
public final String toString() { return key + "=" + value; }
// 键的 hash 值 ^ 值的 hash 值
// 这边我们其他的可以不了解,但是 String 的 hash 算法必须了解。
public final int hashCode() {
return Objects.hashCode(key) ^ Objects.hashCode(value);
}
public final V setValue(V newValue) {
V oldValue = value;
value = newValue;
return oldValue;
}
// 两个节点的比较,先比较地址,否则如果是 Map.Entry 则分别比较键和值
public final boolean equals(Object o) {
if (o == this)
return true;
if (o instanceof Map.Entry) {
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
if (Objects.equals(key, e.getKey()) &&
Objects.equals(value, e.getValue()))
return true;
}
return false;
}
}
看完了内部存储键值对的静态内部类,接下来看静态方法:
// 查看某个键的 hash 值,在基础的 hashCode() 方法后又对其进行了处理
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
// x 如果直接实现了 comparable 接口,就返回 x 的 Class,否则返回 Null
static Class<?> comparableClassFor(Object x) {
...
}
// 如果 x 是 kc 类型,返回 k.compareTo(x) 的结果,否则返回 0
static int compareComparables(Class<?> kc, Object k, Object x) {
return (x == null || x.getClass() != kc ? 0 :
((Comparable)k).compareTo(x));
}
// 这边是返回最小的大于 cap 的 2 的幂次,比如说 cap 为 3 则结果是 4, cap 为 5 则结果是 8 。|= 就是按位或后赋值。
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
接下来是一些变量属性:
// 表结构是存储的内容
transient Node<K,V>[] table;
//
transient Set<Map.Entry<K,V>> entrySet;
// 键值对数量
transient int size;
// 当发生结构性变化时增加,用于表面遍历时对HashMap进行修改操作
transient int modCount;
// 下一次 resize 的值
int threshold;
// hash table 的装载因子
final float loadFactor;
再下面是 public 的操作:
/**
* 构造函数们
*/
// 传入初始容量和装载因子的构造函数,这里可以看到,initialCapacity 并不是直接去创建这个大小的数组,而是使用 tableSizeFor 函数后传递给了 threshold 属性
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
// 传入初始容量,并使用默认的装载因子调用上面的构造函数
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
// 无参的构造函数,默认调用
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
// 将 m 的节点放入表或者树中
public HashMap(Map<? extends K, ? extends V> m) {
this.loadFactor = DEFAULT_LOAD_FACTOR;
putMapEntries(m, false);
}
// 实现了 Map 接口中的 putAll 方法
final void putMapEntries(Map<? extends K, ? extends V> m, boolean evict) {
// 获取 m 的大小
int s = m.size();
if (s > 0) {
// 当 HashMap 为空时,也就是没有内容时,计算 t 和 threshhold进行比较
if (table == null) { // pre-size
float ft = ((float)s / loadFactor) + 1.0F;
int t = ((ft < (float)MAXIMUM_CAPACITY) ?
(int)ft : MAXIMUM_CAPACITY);
if (t > threshold)
threshold = tableSizeFor(t);
}
// 如果 m 的大小比下一次 resize 的值要大,直接 resize
else if (s > threshold)
resize();
// 遍历 m 将节点进行保存
for (Map.Entry<? extends K, ? extends V> e : m.entrySet()) {
K key = e.getKey();
V value = e.getValue();
putVal(hash(key), key, value, false, evict);
}
}
}
// 返回键值对数量
public int size() {
return size;
}
// 返回键值对数量是否为0(即 HashMap 是否还没有键值对)
public boolean isEmpty() {
return size == 0;
}
// 通过 getNode 的方法获取对应 key 的节点的 value
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
// 利用 key 的 hash 值以及 key 获取对应 key 的 Node
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
// 这个判断有三部分,第一部分判断存储数组是否为空,第二部分判断数组长度是否为0,第三部分判断 (n-1) & hash 值的位置是否存在该 key 对应的节点(这样主要是因为 put 的时候就是这么存的)
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
// 如果 key 的 hash 值和对应节点 key 的 hash 值相等并且 key 相等或者 equals 之后相等且不为 null,则返回该节点
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
// 如果上面的不成立,并且 first 节点上有 next(next 应该是解决 hash 冲突的解决方案)
if ((e = first.next) != null) {
// 如果是 TreeNode(表明是红黑树的结构),那么利用 hash 值和 key 找到红黑树中的节点
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
// 否则,不断的找冲突解决方案中的 next 直到找到对应节点或者找完
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
// 利用 key 和 getNode 方法找到节点,没找到就没有该 key 对应的节点
public boolean containsKey(Object key) {
return getNode(hash(key), key) != null;
}
// 插入键值对
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
// 插入键值对的实际方法
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
// 如果存储数组为 null 或者数组长度为0,那么将存储从结构 resize 一下后赋值给数组并将长度赋值给 n
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// 如果对应的地方没有节点,那么新建节点并赋值到数组的对应位置
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
// 如果对应地方有节点,那么只可能有两种情况:1、对应的键存在,那么修改值;2、表结构起冲突了不够存了,要么在该节点的位置增加 next 冲突节点,或者转换成树结构的 putval 方法
else {
Node<K,V> e; K k;
// 表结构对应位置存在对应的 key 的节点,那么将 e 赋值成为该节点
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
// 如果表结构对应位置的 key 跟说好的不一样,并且该位置是个 TreeNode,那么调用树结构的 putVal 操作
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
// 如果是该位置不是树结构的节点并且跟说好的不一样,那么在
else {
for (int binCount = 0; ; ++binCount) {
// 本身该位置的节点没有冲突节点,那么加冲突节点
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
// 找到该位置冲突节点中需要的值了,赋值给 e
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
// 对已经有的对应 key 的键值对,进行值的替换并返回旧的值
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
// 这边是一个回调函数,对节点进行修改后会调用这个函数,HashMap中没有定义具体方法
afterNodeAccess(e);
return oldValue;
}
}
// 新增节点后的处理工作:增加修改次数、增加键值对数量并决定要不要 resize、增加节点后的方法(同样是回调函数,HashMap中没定义)
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
// resize 方法是将数组进行扩容,不是将表结构转换成树结构
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
// 如果原本的长度大于等于最大值,就把 threshold设置成最大值
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// 否则将新长度变成旧长度 * 2, 将 threshold * 2
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
// 如果原来容量为0,那么把原来的 threshold 赋值给新的容量
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
// 如果原来的 threshold 为0,那么使用默认值进行赋值
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
// 如果新的 threshold 为0,就使用默认值计算出新的 threshold
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
// 创建一个新的容量的数组
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
// 下面循环做的就是将旧的数组中的节点全部放到新的数组中去
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
// 如果原来的数组长度小于最小变成树的值,那么 resize,否则把指定 hash 位置的普通的 Node 转化成 TreeNode(TreeNode也是个静态内部类,是红黑树的节点)
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
else if ((e = tab[index = (n - 1) & hash]) != null) {
TreeNode<K,V> hd = null, tl = null;
do {
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
// 把这个节点和其相关节点变成树
hd.treeify(tab);
}
}
// 就调用了前面的方法,目的是把 m 的值放到当前 map 中
public void putAll(Map<? extends K, ? extends V> m) {
putMapEntries(m, true);
}
// 删除这个 key 对应的节点,调用了后面的 removeNode 方法
public V remove(Object key) {
Node<K,V> e;
return (e = removeNode(hash(key), key, null, false, true)) == null ?
null : e.value;
}
// 删除对应 key,value 的节点
final Node<K,V> removeNode(int hash, Object key, Object value,
boolean matchValue, boolean movable) {
Node<K,V>[] tab; Node<K,V> p; int n, index;
if ((tab = table) != null && (n = tab.length) > 0 &&
(p = tab[index = (n - 1) & hash]) != null) {
Node<K,V> node = null, e; K k; V v;
// 如果这个 hash 位置的第一个节点就是对应 key 的节点
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
node = p;
// 找这个 hash 位置其他的节点
else if ((e = p.next) != null) {
// 如果是树节点,用 getTreeNode 获取到节点
if (p instanceof TreeNode)
node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
// 如果是普通节点,那么遍历下去
else {
do {
if (e.hash == hash &&
((k = e.key) == key ||
(key != null && key.equals(k)))) {
node = e;
break;
}
p = e;
} while ((e = e.next) != null);
}
}
// 删除节点的逻辑,这边有个标志位 matchValue,用于判断需不需要考虑 value 的对应
if (node != null && (!matchValue || (v = node.value) == value ||
(value != null && value.equals(v)))) {
// 考虑到树节点删除对于树的结构性改变,使用 removeTreeNode方法
if (node instanceof TreeNode)
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
// 当前 hash 位置只有一个节点,直接把要删除节点的 next 放到数组的这个 hash 位置
else if (node == p)
tab[index] = node.next;
// 当前 hash 位置不止一个节点,直接使用链表中删除节点的方法
else
p.next = node.next;
++modCount;
--size;
afterNodeRemoval(node);
return node;
}
}
return null;
}
// 清空所有节点,但是数组的长度没变
public void clear() {
Node<K,V>[] tab;
modCount++;
if ((tab = table) != null && size > 0) {
size = 0;
for (int i = 0; i < tab.length; ++i)
tab[i] = null;
}
}
// 遍历所有节点查看是否存在 value 的节点
public boolean containsValue(Object value) {
Node<K,V>[] tab; V v;
if ((tab = table) != null && size > 0) {
for (int i = 0; i < tab.length; ++i) {
for (Node<K,V> e = tab[i]; e != null; e = e.next) {
if ((v = e.value) == value ||
(value != null && value.equals(v)))
return true;
}
}
}
return false;
}
// 返回 KeySet
public Set<K> keySet() {
Set<K> ks = keySet;
if (ks == null) {
ks = new KeySet();
keySet = ks;
}
return ks;
}
// 内部类 KeySet,提供了一些集合常用的方法。因为是继承了 AbstractSet 因此键唯一
final class KeySet extends AbstractSet<K> {
public final int size() { return size; }
public final void clear() { HashMap.this.clear(); }
public final Iterator<K> iterator() { return new KeyIterator(); }
public final boolean contains(Object o) { return containsKey(o); }
public final boolean remove(Object key) {
return removeNode(hash(key), key, null, false, true) != null;
}
public final Spliterator<K> spliterator() {
return new KeySpliterator<>(HashMap.this, 0, -1, 0, 0);
}
public final void forEach(Consumer<? super K> action) {
Node<K,V>[] tab;
if (action == null)
throw new NullPointerException();
if (size > 0 && (tab = table) != null) {
int mc = modCount;
for (int i = 0; i < tab.length; ++i) {
for (Node<K,V> e = tab[i]; e != null; e = e.next)
action.accept(e.key);
}
if (modCount != mc)
throw new ConcurrentModificationException();
}
}
}
// 和上面 KeySet 相对应,返回 value 的集合
public Collection<V> values() {
Collection<V> vs = values;
if (vs == null) {
vs = new Values();
values = vs;
}
return vs;
}
// 内部类 Values,提供了 value 的集合
final class Values extends AbstractCollection<V> {
public final int size() { return size; }
public final void clear() { HashMap.this.clear(); }
public final Iterator<V> iterator() { return new ValueIterator(); }
public final boolean contains(Object o) { return containsValue(o); }
public final Spliterator<V> spliterator() {
return new ValueSpliterator<>(HashMap.this, 0, -1, 0, 0);
}
public final void forEach(Consumer<? super V> action) {
Node<K,V>[] tab;
if (action == null)
throw new NullPointerException();
if (size > 0 && (tab = table) != null) {
int mc = modCount;
for (int i = 0; i < tab.length; ++i) {
for (Node<K,V> e = tab[i]; e != null; e = e.next)
action.accept(e.value);
}
if (modCount != mc)
throw new ConcurrentModificationException();
}
}
}
// 返回一个键值对的 set
public Set<Map.Entry<K,V>> entrySet() {
Set<Map.Entry<K,V>> es;
return (es = entrySet) == null ? (entrySet = new EntrySet()) : es;
}
// 内部类 EntrySet,用于记录 map 中的节点
final class EntrySet extends AbstractSet<Map.Entry<K,V>> {
public final int size() { return size; }
public final void clear() { HashMap.this.clear(); }
public final Iterator<Map.Entry<K,V>> iterator() {
return new EntryIterator();
}
public final boolean contains(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry<?,?> e = (Map.Entry<?,?>) o;
Object key = e.getKey();
Node<K,V> candidate = getNode(hash(key), key);
return candidate != null && candidate.equals(e);
}
public final boolean remove(Object o) {
if (o instanceof Map.Entry) {
Map.Entry<?,?> e = (Map.Entry<?,?>) o;
Object key = e.getKey();
Object value = e.getValue();
return removeNode(hash(key), key, value, true, true) != null;
}
return false;
}
public final Spliterator<Map.Entry<K,V>> spliterator() {
return new EntrySpliterator<>(HashMap.this, 0, -1, 0, 0);
}
public final void forEach(Consumer<? super Map.Entry<K,V>> action) {
Node<K,V>[] tab;
if (action == null)
throw new NullPointerException();
if (size > 0 && (tab = table) != null) {
int mc = modCount;
for (int i = 0; i < tab.length; ++i) {
for (Node<K,V> e = tab[i]; e != null; e = e.next)
action.accept(e);
}
if (modCount != mc)
throw new ConcurrentModificationException();
}
}
}
// 返回指定 key 的 value,如果没有则返回默认值 defaultValue
public V getOrDefault(Object key, V defaultValue) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? defaultValue : e.value;
}
// 对应 key 没有 value 时更新,否则返回已有的 value
@Override
public V putIfAbsent(K key, V value) {
return putVal(hash(key), key, value, true, true);
}
// 删除节点,成功返回 true,没有返回 false
@Override
public boolean remove(Object key, Object value) {
return removeNode(hash(key), key, value, true, true) != null;
}
// 将对应键值对的 node 更改 value
@Override
public boolean replace(K key, V oldValue, V newValue) {
Node<K,V> e; V v;
if ((e = getNode(hash(key), key)) != null &&
((v = e.value) == oldValue || (v != null && v.equals(oldValue)))) {
e.value = newValue;
afterNodeAccess(e);
return true;
}
return false;
}
// 对应键的 node 更改 value
@Override
public V replace(K key, V value) {
Node<K,V> e;
if ((e = getNode(hash(key), key)) != null) {
V oldValue = e.value;
e.value = value;
afterNodeAccess(e);
return oldValue;
}
return null;
}
// 传入一个 Function,对应 key 的值如果没有则更新为对 key 进行 Function 运算的结果,否则返回原来的 value
@Override
public V computeIfAbsent(K key,
Function<? super K, ? extends V> mappingFunction) {
if (mappingFunction == null)
throw new NullPointerException();
int hash = hash(key);
Node<K,V>[] tab; Node<K,V> first; int n, i;
int binCount = 0;
TreeNode<K,V> t = null;
Node<K,V> old = null;
// 下面是先找到对应 key 的节点
if (size > threshold || (tab = table) == null ||
(n = tab.length) == 0)
n = (tab = resize()).length;
if ((first = tab[i = (n - 1) & hash]) != null) {
if (first instanceof TreeNode)
old = (t = (TreeNode<K,V>)first).getTreeNode(hash, key);
else {
Node<K,V> e = first; K k;
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k)))) {
old = e;
break;
}
++binCount;
} while ((e = e.next) != null);
}
V oldValue;
if (old != null && (oldValue = old.value) != null) {
afterNodeAccess(old);
return oldValue;
}
}
// value 是对 key 进行 Function 中的运算后的结果
V v = mappingFunction.apply(key);
if (v == null) {
return null;
} else if (old != null) {
old.value = v;
afterNodeAccess(old);
return v;
}
else if (t != null)
t.putTreeVal(this, tab, hash, key, v);
else {
tab[i] = newNode(hash, key, v, first);
if (binCount >= TREEIFY_THRESHOLD - 1)
treeifyBin(tab, hash);
}
++modCount;
++size;
afterNodeInsertion(true);
return v;
}
// 当对应 key 的 node 存在,进行传入的 BitFunction
public V computeIfPresent(K key,
BiFunction<? super K, ? super V, ? extends V> remappingFunction) {
if (remappingFunction == null)
throw new NullPointerException();
Node<K,V> e; V oldValue;
int hash = hash(key);
if ((e = getNode(hash, key)) != null &&
(oldValue = e.value) != null) {
V v = remappingFunction.apply(key, oldValue);
if (v != null) {
e.value = v;
afterNodeAccess(e);
return v;
}
else
// 如果运算结果是 null,删除节点
removeNode(hash, key, null, false, true);
}
}
//
public V compute(K key,
BiFunction<? super K, ? super V, ? extends V> remappingFunction) {
if (remappingFunction == null)
throw new NullPointerException();
int hash = hash(key);
Node<K,V>[] tab; Node<K,V> first; int n, i;
int binCount = 0;
TreeNode<K,V> t = null;
Node<K,V> old = null;
// 找到对应 key 的节点
if (size > threshold || (tab = table) == null ||
(n = tab.length) == 0)
n = (tab = resize()).length;
if ((first = tab[i = (n - 1) & hash]) != null) {
if (first instanceof TreeNode)
old = (t = (TreeNode<K,V>)first).getTreeNode(hash, key);
else {
Node<K,V> e = first; K k;
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k)))) {
old = e;
break;
}
++binCount;
} while ((e = e.next) != null);
}
}
V oldValue = (old == null) ? null : old.value;
// 如果找到了节点,用 key 和 value 进行计算并赋值给 value 或者 v 为 null时删除节点
// 没找到节点但是计算的 v 不为null,那么更新树节点???
V v = remappingFunction.apply(key, oldValue);
if (old != null) {
if (v != null) {
old.value = v;
afterNodeAccess(old);
}
else
// 如果运算结果是 null,删除节点
removeNode(hash, key, null, false, true);
}
else if (v != null) {
if (t != null)
t.putTreeVal(this, tab, hash, key, v);
else {
tab[i] = newNode(hash, key, v, first);
if (binCount >= TREEIFY_THRESHOLD - 1)
treeifyBin(tab, hash);
}
++modCount;
++size;
afterNodeInsertion(true);
}
return v;
}
// 找到对应 key 的节点,将节点的值 oldValue 和参数 value 进行运算,并赋值给节点的值。
@Override
public V merge(K key, V value,
BiFunction<? super V, ? super V, ? extends V> remappingFunction) {
if (value == null)
throw new NullPointerException();
if (remappingFunction == null)
throw new NullPointerException();
int hash = hash(key);
Node<K,V>[] tab; Node<K,V> first; int n, i;
int binCount = 0;
TreeNode<K,V> t = null;
Node<K,V> old = null;
// 找到节点(ps:每个函数都用,为啥不干脆抽出来?)
if (size > threshold || (tab = table) == null ||
(n = tab.length) == 0)
n = (tab = resize()).length;
if ((first = tab[i = (n - 1) & hash]) != null) {
if (first instanceof TreeNode)
old = (t = (TreeNode<K,V>)first).getTreeNode(hash, key);
else {
Node<K,V> e = first; K k;
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k)))) {
old = e;
break;
}
++binCount;
} while ((e = e.next) != null);
}
}
if (old != null) {
V v;
// 将节点的 value 和输入的参数 value 进行计算
if (old.value != null)
v = remappingFunction.apply(old.value, value);
else
v = value;
// 如果计算结果不为 null,赋值给该节点
if (v != null) {
old.value = v;
afterNodeAccess(old);
}
else
// 否则删除节点
removeNode(hash, key, null, false, true);
return v;
}
// 这边通过 putVal 去赋值?为什么?
if (value != null) {
if (t != null)
t.putTreeVal(this, tab, hash, key, value);
else {
tab[i] = newNode(hash, key, value, first);
if (binCount >= TREEIFY_THRESHOLD - 1)
treeifyBin(tab, hash);
}
++modCount;
++size;
afterNodeInsertion(true);
}
return value;
}
// 遍历每个节点并对其进行 action.accept 的操作
@Override
public void forEach(BiConsumer<? super K, ? super V> action) {
Node<K,V>[] tab;
if (action == null)
throw new NullPointerException();
if (size > 0 && (tab = table) != null) {
int mc = modCount;
for (int i = 0; i < tab.length; ++i) {
for (Node<K,V> e = tab[i]; e != null; e = e.next)
action.accept(e.key, e.value);
}
if (modCount != mc)
throw new ConcurrentModificationException();
}
}
// 遍历每个节点,将 value 转化成 function.apply 操作的结果
@Override
public void replaceAll(BiFunction<? super K, ? super V, ? extends V> function) {
Node<K,V>[] tab;
if (function == null)
throw new NullPointerException();
if (size > 0 && (tab = table) != null) {
int mc = modCount;
for (int i = 0; i < tab.length; ++i) {
for (Node<K,V> e = tab[i]; e != null; e = e.next) {
e.value = function.apply(e.key, e.value);
}
}
if (modCount != mc)
throw new ConcurrentModificationException();
}
}
下面是实现另外两个接口中的方法,即Cloneable和Serializable的方法:
// clone 函数
@Override
public Object clone() {
HashMap<K,V> result;
try {
result = (HashMap<K,V>)super.clone();
} catch (CloneNotSupportedException e) {
// this shouldn‘t happen, since we are Cloneable
throw new InternalError(e);
}
result.reinitialize();
result.putMapEntries(this, false);
return result;
}
// 返回装载因子和容量(数组非空则返回数组长度,否则返回 threshold 或者默认初始化容量)
final float loadFactor() { return loadFactor; }
final int capacity() {
return (table != null) ? table.length :
(threshold > 0) ? threshold :
DEFAULT_INITIAL_CAPACITY;
}
// 前面存储的 table 使用 transient 修饰的,因此没法持久化,这边自己实现了 writeObject 和 readObject 方法来完成持久化和反持久化
private void writeObject(java.io.ObjectOutputStream s)
throws IOException {
...
}
private void readObject(java.io.ObjectInputStream s)
throws IOException, ClassNotFoundException {
...
}
下面是几个迭代器类,用于键啊、值、节点的迭代:
// 抽象类,用于下面被继承
abstract class HashIterator {
Node<K,V> next; // next entry to return
Node<K,V> current; // current entry
int expectedModCount; // for fast-fail
int index; // current slot
// 构造函数
HashIterator() {
// 将外部类(HashMap)的修改次数赋值给 expectedModCount
expectedModCount = modCount;
Node<K,V>[] t = table;
current = next = null;
index = 0;
if (t != null && size > 0) { // advance to first entry
do {} while (index < t.length && (next = t[index++]) == null);
}
}
public final boolean hasNext() {
return next != null;
}
final Node<K,V> nextNode() {
Node<K,V>[] t;
Node<K,V> e = next;
if (modCount != expectedModCount)
throw new ConcurrentModificationException();
if (e == null)
throw new NoSuchElementException();
// 如果当前表索引的节点遍历完了,取下一个索引的节点作为 next
if ((next = (current = e).next) == null && (t = table) != null) {
do {} while (index < t.length && (next = t[index++]) == null);
}
return e;
}
public final void remove() {
Node<K,V> p = current;
if (p == null)
throw new IllegalStateException();
if (modCount != expectedModCount)
throw new ConcurrentModificationException();
current = null;
K key = p.key;
// 在迭代器中将节点 remove 掉了,那么外部类中也会 remove
removeNode(hash(key), key, null, false, false);
expectedModCount = modCount;
}
}
// 下面是三个实现,区别只在于 next 函数返回的内容
final class KeyIterator extends HashIterator
implements Iterator<K> {
public final K next() { return nextNode().key; }
}
final class ValueIterator extends HashIterator
implements Iterator<V> {
public final V next() { return nextNode().value; }
}
final class EntryIterator extends HashIterator
implements Iterator<Map.Entry<K,V>> {
public final Map.Entry<K,V> next() { return nextNode(); }
}
下面是几个 spliterator 类(可拆分迭代器):
一个博客介绍了可拆分迭代器是啥。
// 所有 Spliterator 的父类,这边没什么特别的,关键方法都在 Spliterator 接口中,实现子类可以自己重写
static class HashMapSpliterator<K,V> {
final HashMap<K,V> map;
Node<K,V> current; // current node
int index; // current index, modified on advance/split
int fence; // one past last index
int est; // size estimate
int expectedModCount; // for comodification checks
HashMapSpliterator(HashMap<K,V> m, int origin,
int fence, int est,
int expectedModCount) {
this.map = m;
this.index = origin;
this.fence = fence;
this.est = est;
this.expectedModCount = expectedModCount;
}
// 获取 fence,如果小于 0 则返回外部 tab 数组的长度,否则返回 fence
final int getFence() { // initialize fence and size on first use
int hi;
if ((hi = fence) < 0) {
HashMap<K,V> m = map;
est = m.size;
expectedModCount = m.modCount;
Node<K,V>[] tab = m.table;
hi = fence = (tab == null) ? 0 : tab.length;
}
return hi;
}
// 强制初始化并返回 est
public final long estimateSize() {
getFence(); // force init
return (long) est;
}
}
// 键的 Spliterator, 实现了 Spliterator 接口(该接口中说明用于分治遍历元素,元素可以通过 tryAdvance() 方法独立的遍历或者 forEachRemaining() 方法各个分块按顺序遍历)。
static final class KeySpliterator<K,V>
extends HashMapSpliterator<K,V>
implements Spliterator<K> {
KeySpliterator(HashMap<K,V> m, int origin, int fence, int est,
int expectedModCount) {
super(m, origin, fence, est, expectedModCount);
}
// 尝试拆分成出一个新的迭代器
public KeySpliterator<K,V> trySplit() {
int hi = getFence(), lo = index, mid = (lo + hi) >>> 1;
return (lo >= mid || current != null) ? null :
new KeySpliterator<>(map, lo, index = mid, est >>>= 1,
expectedModCount);
}
// 从 current 开始遍历,对节点进行 action.accept 操作,直到没有节点或者 table 的 index 改变了 fence 次(可以认为是经历了 fence 的 bucket)
public void forEachRemaining(Consumer<? super K> action) {
int i, hi, mc;
if (action == null)
throw new NullPointerException();
HashMap<K,V> m = map;
Node<K,V>[] tab = m.table;
if ((hi = fence) < 0) {
mc = expectedModCount = m.modCount;
hi = fence = (tab == null) ? 0 : tab.length;
}
else
mc = expectedModCount;
if (tab != null && tab.length >= hi &&
(i = index) >= 0 && (i < (index = hi) || current != null)) {
Node<K,V> p = current;
current = null;
do {
if (p == null)
p = tab[i++];
else {
action.accept(p.key);
p = p.next;
}
} while (p != null || i < hi);
if (m.modCount != mc)
throw new ConcurrentModificationException();
}
}
// 如果存在剩余元素,则对其执行给定操作,返回true(怎么感觉跟上面一样???)
public boolean tryAdvance(Consumer<? super K> action) {
int hi;
if (action == null)
throw new NullPointerException();
Node<K,V>[] tab = map.table;
if (tab != null && tab.length >= (hi = getFence()) && index >= 0) {
while (current != null || index < hi) {
if (current == null)
current = tab[index++];
else {
K k = current.key;
current = current.next;
action.accept(k);
if (map.modCount != expectedModCount)
throw new ConcurrentModificationException();
return true;
}
}
}
return false;
}
// 返回此 Spliterator 及其元素的一组特性
public int characteristics() {
return (fence < 0 || est == map.size ? Spliterator.SIZED : 0) |
Spliterator.DISTINCT;
}
}
// 各个环节跟 KeySpliterator 类似
static final class ValueSpliterator<K,V>
extends HashMapSpliterator<K,V>
implements Spliterator<V> {
ValueSpliterator(HashMap<K,V> m, int origin, int fence, int est,
int expectedModCount) {
super(m, origin, fence, est, expectedModCount);
}
public ValueSpliterator<K,V> trySplit() {
int hi = getFence(), lo = index, mid = (lo + hi) >>> 1;
return (lo >= mid || current != null) ? null :
new ValueSpliterator<>(map, lo, index = mid, est >>>= 1,
expectedModCount);
}
public void forEachRemaining(Consumer<? super V> action) {
int i, hi, mc;
if (action == null)
throw new NullPointerException();
HashMap<K,V> m = map;
Node<K,V>[] tab = m.table;
if ((hi = fence) < 0) {
mc = expectedModCount = m.modCount;
hi = fence = (tab == null) ? 0 : tab.length;
}
else
mc = expectedModCount;
if (tab != null && tab.length >= hi &&
(i = index) >= 0 && (i < (index = hi) || current != null)) {
Node<K,V> p = current;
current = null;
do {
if (p == null)
p = tab[i++];
else {
action.accept(p.value);
p = p.next;
}
} while (p != null || i < hi);
if (m.modCount != mc)
throw new ConcurrentModificationException();
}
}
public boolean tryAdvance(Consumer<? super V> action) {
int hi;
if (action == null)
throw new NullPointerException();
Node<K,V>[] tab = map.table;
if (tab != null && tab.length >= (hi = getFence()) && index >= 0) {
while (current != null || index < hi) {
if (current == null)
current = tab[index++];
else {
V v = current.value;
current = current.next;
action.accept(v);
if (map.modCount != expectedModCount)
throw new ConcurrentModificationException();
return true;
}
}
}
return false;
}
public int characteristics() {
return (fence < 0 || est == map.size ? Spliterator.SIZED : 0);
}
}
// 同上
static final class EntrySpliterator<K,V>
extends HashMapSpliterator<K,V>
implements Spliterator<Map.Entry<K,V>> {
EntrySpliterator(HashMap<K,V> m, int origin, int fence, int est,
int expectedModCount) {
super(m, origin, fence, est, expectedModCount);
}
public EntrySpliterator<K,V> trySplit() {
int hi = getFence(), lo = index, mid = (lo + hi) >>> 1;
return (lo >= mid || current != null) ? null :
new EntrySpliterator<>(map, lo, index = mid, est >>>= 1,
expectedModCount);
}
public void forEachRemaining(Consumer<? super Map.Entry<K,V>> action) {
int i, hi, mc;
if (action == null)
throw new NullPointerException();
HashMap<K,V> m = map;
Node<K,V>[] tab = m.table;
if ((hi = fence) < 0) {
mc = expectedModCount = m.modCount;
hi = fence = (tab == null) ? 0 : tab.length;
}
else
mc = expectedModCount;
if (tab != null && tab.length >= hi &&
(i = index) >= 0 && (i < (index = hi) || current != null)) {
Node<K,V> p = current;
current = null;
do {
if (p == null)
p = tab[i++];
else {
action.accept(p);
p = p.next;
}
} while (p != null || i < hi);
if (m.modCount != mc)
throw new ConcurrentModificationException();
}
}
public boolean tryAdvance(Consumer<? super Map.Entry<K,V>> action) {
int hi;
if (action == null)
throw new NullPointerException();
Node<K,V>[] tab = map.table;
if (tab != null && tab.length >= (hi = getFence()) && index >= 0) {
while (current != null || index < hi) {
if (current == null)
current = tab[index++];
else {
Node<K,V> e = current;
current = current.next;
action.accept(e);
if (map.modCount != expectedModCount)
throw new ConcurrentModificationException();
return true;
}
}
}
return false;
}
public int characteristics() {
return (fence < 0 || est == map.size ? Spliterator.SIZED : 0) |
Spliterator.DISTINCT;
}
}
下面是针对LinkedHashMap需要重写的方法:
// 创建一个非树节点
Node<K,V> newNode(int hash, K key, V value, Node<K,V> next) {
return new Node<>(hash, key, value, next);
}
// 将一个非树节点转化成树节点
Node<K,V> replacementNode(Node<K,V> p, Node<K,V> next) {
return new Node<>(p.hash, p.key, p.value, next);
}
// 创建一个树节点
TreeNode<K,V> newTreeNode(int hash, K key, V value, Node<K,V> next) {
return new TreeNode<>(hash, key, value, next);
}
// 将一个节点下的节点转换成树形结构
TreeNode<K,V> replacementTreeNode(Node<K,V> p, Node<K,V> next) {
return new TreeNode<>(p.hash, p.key, p.value, next);
}
// 重置默认状态,被 clone() 和 readObject() 调用
void reinitialize() {
table = null;
entrySet = null;
keySet = null;
values = null;
modCount = 0;
threshold = 0;
size = 0;
}
// 回调函数,需要 LinkedHashMap 自己重写
void afterNodeAccess(Node<K,V> p) { }
void afterNodeInsertion(boolean evict) { }
void afterNodeRemoval(Node<K,V> p) { }
// 只被 writeObject() 方法调用,保证顺序
void internalWriteEntries(java.io.ObjectOutputStream s) throws IOException {
Node<K,V>[] tab;
if (size > 0 && (tab = table) != null) {
for (int i = 0; i < tab.length; ++i) {
for (Node<K,V> e = tab[i]; e != null; e = e.next) {
s.writeObject(e.key);
s.writeObject(e.value);
}
}
}
}
后面是树形结构的类和方法:
emmmmmm......由于红黑树不是很懂,这部分就先不看了
/**
* Entry for Tree bins. Extends LinkedHashMap.Entry (which in turn
* extends Node) so can be used as extension of either regular or
* linked node.
*/
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
TreeNode<K,V> parent; // red-black tree links
TreeNode<K,V> left;
TreeNode<K,V> right;
TreeNode<K,V> prev; // needed to unlink next upon deletion
boolean red;
TreeNode(int hash, K key, V val, Node<K,V> next) {
super(hash, key, val, next);
}
/**
* Returns root of tree containing this node.
*/
final TreeNode<K,V> root() {
for (TreeNode<K,V> r = this, p;;) {
if ((p = r.parent) == null)
return r;
r = p;
}
}
/**
* Ensures that the given root is the first node of its bin.
*/
static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {
int n;
if (root != null && tab != null && (n = tab.length) > 0) {
int index = (n - 1) & root.hash;
TreeNode<K,V> first = (TreeNode<K,V>)tab[index];
if (root != first) {
Node<K,V> rn;
tab[index] = root;
TreeNode<K,V> rp = root.prev;
if ((rn = root.next) != null)
((TreeNode<K,V>)rn).prev = rp;
if (rp != null)
rp.next = rn;
if (first != null)
first.prev = root;
root.next = first;
root.prev = null;
}
assert checkInvariants(root);
}
}
/**
* Finds the node starting at root p with the given hash and key.
* The kc argument caches comparableClassFor(key) upon first use
* comparing keys.
*/
final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
TreeNode<K,V> p = this;
do {
int ph, dir; K pk;
TreeNode<K,V> pl = p.left, pr = p.right, q;
if ((ph = p.hash) > h)
p = pl;
else if (ph < h)
p = pr;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
else if (pl == null)
p = pr;
else if (pr == null)
p = pl;
else if ((kc != null ||
(kc = comparableClassFor(k)) != null) &&
(dir = compareComparables(kc, k, pk)) != 0)
p = (dir < 0) ? pl : pr;
else if ((q = pr.find(h, k, kc)) != null)
return q;
else
p = pl;
} while (p != null);
return null;
}
/**
* Calls find for root node.
*/
final TreeNode<K,V> getTreeNode(int h, Object k) {
return ((parent != null) ? root() : this).find(h, k, null);
}
/**
* Tie-breaking utility for ordering insertions when equal
* hashCodes and non-comparable. We don‘t require a total
* order, just a consistent insertion rule to maintain
* equivalence across rebalancings. Tie-breaking further than
* necessary simplifies testing a bit.
*/
static int tieBreakOrder(Object a, Object b) {
int d;
if (a == null || b == null ||
(d = a.getClass().getName().
compareTo(b.getClass().getName())) == 0)
d = (System.identityHashCode(a) <= System.identityHashCode(b) ?
-1 : 1);
return d;
}
/**
* Forms tree of the nodes linked from this node.
* @return root of tree
*/
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
for (TreeNode<K,V> x = this, next; x != null; x = next) {
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
if (root == null) {
x.parent = null;
x.red = false;
root = x;
}
else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
for (TreeNode<K,V> p = root;;) {
int dir, ph;
K pk = p.key;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp;
if (dir <= 0)
xp.left = x;
else
xp.right = x;
root = balanceInsertion(root, x);
break;
}
}
}
}
moveRootToFront(tab, root);
}
/**
* Returns a list of non-TreeNodes replacing those linked from
* this node.
*/
final Node<K,V> untreeify(HashMap<K,V> map) {
Node<K,V> hd = null, tl = null;
for (Node<K,V> q = this; q != null; q = q.next) {
Node<K,V> p = map.replacementNode(q, null);
if (tl == null)
hd = p;
else
tl.next = p;
tl = p;
}
return hd;
}
/**
* Tree version of putVal.
*/
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {
Class<?> kc = null;
boolean searched = false;
TreeNode<K,V> root = (parent != null) ? root() : this;
for (TreeNode<K,V> p = root;;) {
int dir, ph; K pk;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
if (!searched) {
TreeNode<K,V> q, ch;
searched = true;
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
dir = tieBreakOrder(k, pk);
}
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
Node<K,V> xpn = xp.next;
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
if (dir <= 0)
xp.left = x;
else
xp.right = x;
xp.next = x;
x.parent = x.prev = xp;
if (xpn != null)
((TreeNode<K,V>)xpn).prev = x;
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}
/**
* Removes the given node, that must be present before this call.
* This is messier than typical red-black deletion code because we
* cannot swap the contents of an interior node with a leaf
* successor that is pinned by "next" pointers that are accessible
* independently during traversal. So instead we swap the tree
* linkages. If the current tree appears to have too few nodes,
* the bin is converted back to a plain bin. (The test triggers
* somewhere between 2 and 6 nodes, depending on tree structure).
*/
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,
boolean movable) {
int n;
if (tab == null || (n = tab.length) == 0)
return;
int index = (n - 1) & hash;
TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;
TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;
if (pred == null)
tab[index] = first = succ;
else
pred.next = succ;
if (succ != null)
succ.prev = pred;
if (first == null)
return;
if (root.parent != null)
root = root.root();
if (root == null || root.right == null ||
(rl = root.left) == null || rl.left == null) {
tab[index] = first.untreeify(map); // too small
return;
}
TreeNode<K,V> p = this, pl = left, pr = right, replacement;
if (pl != null && pr != null) {
TreeNode<K,V> s = pr, sl;
while ((sl = s.left) != null) // find successor
s = sl;
boolean c = s.red; s.red = p.red; p.red = c; // swap colors
TreeNode<K,V> sr = s.right;
TreeNode<K,V> pp = p.parent;
if (s == pr) { // p was s‘s direct parent
p.parent = s;
s.right = p;
}
else {
TreeNode<K,V> sp = s.parent;
if ((p.parent = sp) != null) {
if (s == sp.left)
sp.left = p;
else
sp.right = p;
}
if ((s.right = pr) != null)
pr.parent = s;
}
p.left = null;
if ((p.right = sr) != null)
sr.parent = p;
if ((s.left = pl) != null)
pl.parent = s;
if ((s.parent = pp) == null)
root = s;
else if (p == pp.left)
pp.left = s;
else
pp.right = s;
if (sr != null)
replacement = sr;
else
replacement = p;
}
else if (pl != null)
replacement = pl;
else if (pr != null)
replacement = pr;
else
replacement = p;
if (replacement != p) {
TreeNode<K,V> pp = replacement.parent = p.parent;
if (pp == null)
root = replacement;
else if (p == pp.left)
pp.left = replacement;
else
pp.right = replacement;
p.left = p.right = p.parent = null;
}
TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);
if (replacement == p) { // detach
TreeNode<K,V> pp = p.parent;
p.parent = null;
if (pp != null) {
if (p == pp.left)
pp.left = null;
else if (p == pp.right)
pp.right = null;
}
}
if (movable)
moveRootToFront(tab, r);
}
/**
* Splits nodes in a tree bin into lower and upper tree bins,
* or untreeifies if now too small. Called only from resize;
* see above discussion about split bits and indices.
*
* @param map the map
* @param tab the table for recording bin heads
* @param index the index of the table being split
* @param bit the bit of hash to split on
*/
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
TreeNode<K,V> b = this;
// Relink into lo and hi lists, preserving order
TreeNode<K,V> loHead = null, loTail = null;
TreeNode<K,V> hiHead = null, hiTail = null;
int lc = 0, hc = 0;
for (TreeNode<K,V> e = b, next; e != null; e = next) {
next = (TreeNode<K,V>)e.next;
e.next = null;
if ((e.hash & bit) == 0) {
if ((e.prev = loTail) == null)
loHead = e;
else
loTail.next = e;
loTail = e;
++lc;
}
else {
if ((e.prev = hiTail) == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
++hc;
}
}
if (loHead != null) {
if (lc <= UNTREEIFY_THRESHOLD)
tab[index] = loHead.untreeify(map);
else {
tab[index] = loHead;
if (hiHead != null) // (else is already treeified)
loHead.treeify(tab);
}
}
if (hiHead != null) {
if (hc <= UNTREEIFY_THRESHOLD)
tab[index + bit] = hiHead.untreeify(map);
else {
tab[index + bit] = hiHead;
if (loHead != null)
hiHead.treeify(tab);
}
}
}
/* ------------------------------------------------------------ */
// Red-black tree methods, all adapted from CLR
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> r, pp, rl;
if (p != null && (r = p.right) != null) {
if ((rl = p.right = r.left) != null)
rl.parent = p;
if ((pp = r.parent = p.parent) == null)
(root = r).red = false;
else if (pp.left == p)
pp.left = r;
else
pp.right = r;
r.left = p;
p.parent = r;
}
return root;
}
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> l, pp, lr;
if (p != null && (l = p.left) != null) {
if ((lr = p.left = l.right) != null)
lr.parent = p;
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
l.right = p;
p.parent = l;
}
return root;
}
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
x.red = true;
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
else if (!xp.red || (xpp = xp.parent) == null)
return root;
if (xp == (xppl = xpp.left)) {
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
if (x == xp.right) {
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateRight(root, xpp);
}
}
}
}
else {
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root,
TreeNode<K,V> x) {
for (TreeNode<K,V> xp, xpl, xpr;;) {
if (x == null || x == root)
return root;
else if ((xp = x.parent) == null) {
x.red = false;
return x;
}
else if (x.red) {
x.red = false;
return root;
}
else if ((xpl = xp.left) == x) {
if ((xpr = xp.right) != null && xpr.red) {
xpr.red = false;
xp.red = true;
root = rotateLeft(root, xp);
xpr = (xp = x.parent) == null ? null : xp.right;
}
if (xpr == null)
x = xp;
else {
TreeNode<K,V> sl = xpr.left, sr = xpr.right;
if ((sr == null || !sr.red) &&
(sl == null || !sl.red)) {
xpr.red = true;
x = xp;
}
else {
if (sr == null || !sr.red) {
if (sl != null)
sl.red = false;
xpr.red = true;
root = rotateRight(root, xpr);
xpr = (xp = x.parent) == null ?
null : xp.right;
}
if (xpr != null) {
xpr.red = (xp == null) ? false : xp.red;
if ((sr = xpr.right) != null)
sr.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateLeft(root, xp);
}
x = root;
}
}
}
else { // symmetric
if (xpl != null && xpl.red) {
xpl.red = false;
xp.red = true;
root = rotateRight(root, xp);
xpl = (xp = x.parent) == null ? null : xp.left;
}
if (xpl == null)
x = xp;
else {
TreeNode<K,V> sl = xpl.left, sr = xpl.right;
if ((sl == null || !sl.red) &&
(sr == null || !sr.red)) {
xpl.red = true;
x = xp;
}
else {
if (sl == null || !sl.red) {
if (sr != null)
sr.red = false;
xpl.red = true;
root = rotateLeft(root, xpl);
xpl = (xp = x.parent) == null ?
null : xp.left;
}
if (xpl != null) {
xpl.red = (xp == null) ? false : xp.red;
if ((sl = xpl.left) != null)
sl.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateRight(root, xp);
}
x = root;
}
}
}
}
}
/**
* Recursive invariant check
*/
static <K,V> boolean checkInvariants(TreeNode<K,V> t) {
TreeNode<K,V> tp = t.parent, tl = t.left, tr = t.right,
tb = t.prev, tn = (TreeNode<K,V>)t.next;
if (tb != null && tb.next != t)
return false;
if (tn != null && tn.prev != t)
return false;
if (tp != null && t != tp.left && t != tp.right)
return false;
if (tl != null && (tl.parent != t || tl.hash > t.hash))
return false;
if (tr != null && (tr.parent != t || tr.hash < t.hash))
return false;
if (t.red && tl != null && tl.red && tr != null && tr.red)
return false;
if (tl != null && !checkInvariants(tl))
return false;
if (tr != null && !checkInvariants(tr))
return false;
return true;
}
}
以上是关于HashMap源码解读(中篇)的主要内容,如果未能解决你的问题,请参考以下文章