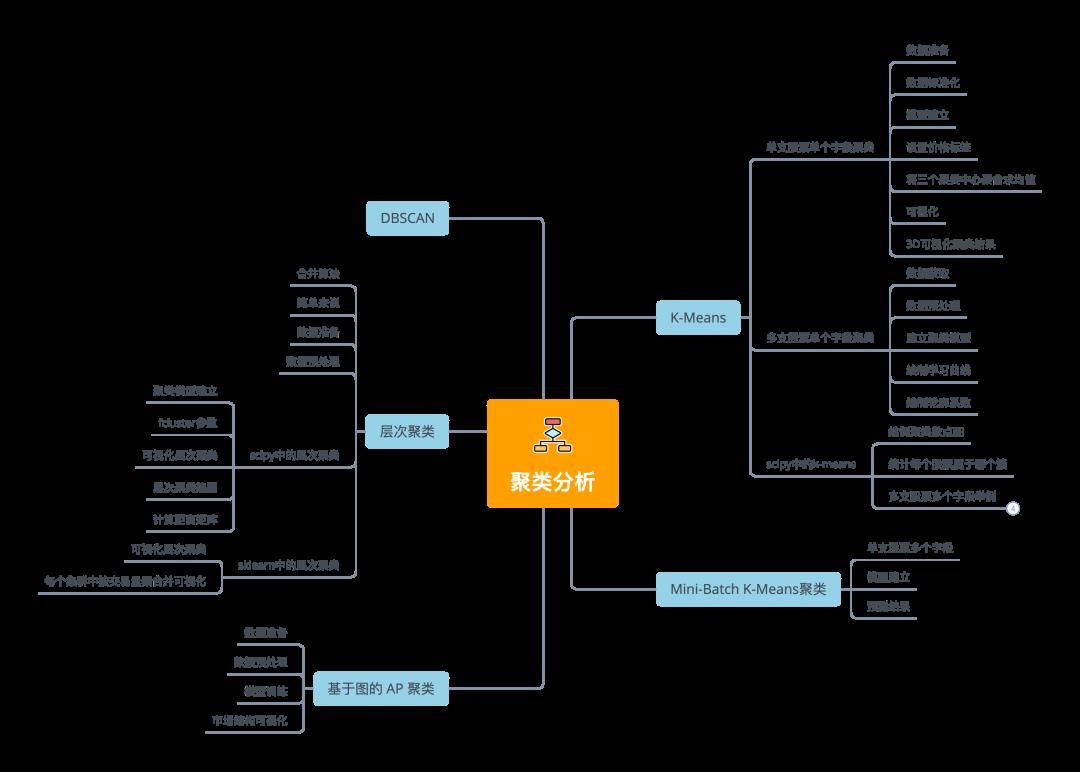
我总结了五种常用聚类分析算法，推荐收藏

Posted 2022-07-15 我爱Python数据挖掘

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了我总结了五种常用聚类分析算法，推荐收藏相关的知识，希望对你有一定的参考价值。

大量数据中具有"相似"特征的数据点或样本划分为一个类别。聚类分析提供了样本集在非监督模式下的类别划分。

基本思想

物以类聚、人以群分

常用于数据探索或挖掘前期

没有先验经验做探索性分析
样本量较大时做预处理

解决问题

数据集可以分几类
每个类别有多少样本量
不同类别中各个变量的强弱关系如何
不同类型的典型特征是什么

应用

群类别间的差异性特征分析
群类别内的关键特征提取
图像压缩、分割、图像理解
异常检测
数据离散化

缺点: 无法提供明确的行动指向; 数据异常对结果有影响。

限于篇幅，完整源码、技术交流，文末获取

K-Means 聚类

K-Means算法的思想简单，对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大。

均值聚类是一种矢量量化方法，起源于信号处理，是数据挖掘中流行的聚类分析方法。

算法原理

随机K个质心；
开始循环，计算每个样本点到那个质心到距离，样本离哪个近就将该样本分给哪个质心，得到K个簇；
对于每个簇，计算所有被分到该簇的样本点的平均距离作为新的质心；
直到所有簇不再发生变化。

衡量指标

组内平方和：Total_Inertia
轮廓系数：组内差异，组间差异取值范围越大越好

优化目标

内差异小，簇间差异大；其中差异由样本点到其所在簇的质心的距离衡量

应用

客户分群、用户画像、精确营销、基于聚类的推荐系统

K-Means算法的优点

k-means算法是解决聚类问题的一种经典算法，算法简单、快速。
算法尝试找出使平方误差函数值最小的k个划分。当簇是密集的、球状或团状的，且簇与簇之间区别明显时，聚类效果较好。

缺点

k-means方法只有在簇的平均值被定义的情况下才能使用，且对有些分类属性的数据不适合。
要求用户必须事先给出要生成的簇的数目k。
对初值敏感，对于不同的初始值，可能会导致不同的聚类结果。
不适合于发现非凸面形状的簇，或者大小差别很大的簇。
对于"噪声"和孤立点数据敏感，少量的该类数据能够对平均值产生极大影响。

单支股票单个字段聚类

仍然以股市数据为例，根据每支股票整个时间段内的股价特征，将相似的那些交易日打上标签，并通过可视化方式将整个时间段内的交易日开盘价与收盘价展现出来。

数据准备

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
import yfinance as yf
yf.pdr_override()

symbol = 'TCEHY'
start = '2020-01-01'
end = '2021-01-01'

dataset = yf.download(symbol,start,end)
dataset.head()

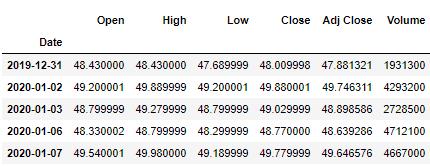
数据标准化

X = dataset[['Open','High','Low','Close','Adj Close','Volume']]
from sklearn.preprocessing import StandardScaler
X = dataset.values[:,1:]
X = np.nan_to_num(X)
Clus_dataSet = StandardScaler().fit_transform(X)
Clus_dataSet

array([[-1.33493398, -1.31490333, -1.33543485, 
        -1.33612775, -0.95734284],
       [-1.19325204, -1.16643501, -1.15260357, 
        -1.15474442,  0.23740018],
       ...,
       [ 0.99796748,  1.03600566,  0.98270623,  
         0.98235044, -0.41634718],
       [ 1.0222281 ,  0.97701185,  0.99932706,  
         0.99888395, -0.63830968]])

模型建立

from sklearn.cluster import KMeans 
# 设置簇中心个数
clusterNum = 3
k_means = KMeans(init = "k-means++", 
                 n_clusters = clusterNum,
                 n_init = 12)
k_means.fit(X)
labels = k_means.labels_
print(labels)

[1 0 1 0 0 1 1 0...1 1]

设置价格标签

dataset["Prices"] = labels
dataset.head(5)

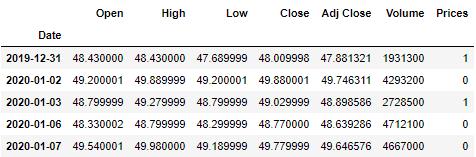
将三个聚类中心聚合求均值

dataset.groupby('Prices').mean()

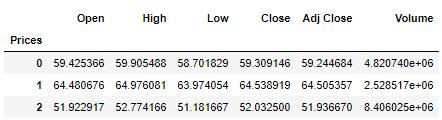
可视化

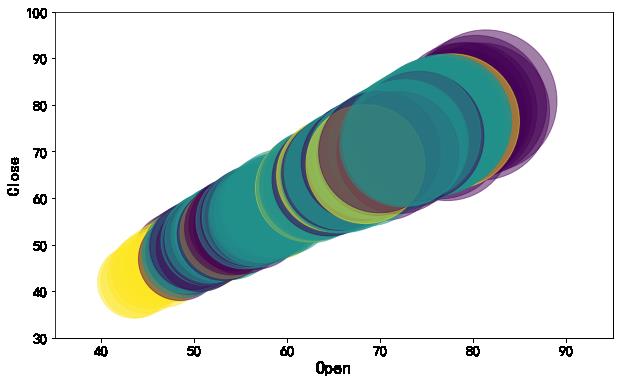
以类别为颜色，开盘价为散点的面积绘制开盘价和收盘价的气泡图。

area = np.pi * ( X[:, 1])**2  
plt.figure(figsize=(10,6))
plt.scatter(X[:, 0], X[:, 3], s=area, 
            c=labels.astype(np.float), 
            alpha=0.5)
plt.xlabel('Open', fontsize=18)
plt.ylabel('Close', fontsize=16)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.xlim([35,95])
plt.ylim([30,100])
plt.show()

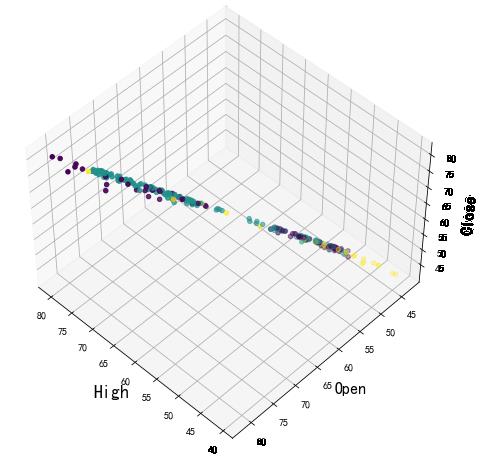
3D可视化聚类结果

from mpl_toolkits.mplot3d import Axes3D 
fig = plt.figure(1, figsize=(8, 6))
plt.clf() # Clear figure
# 设置3d画布
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
plt.cla() # Clear axis
ax.set_xlabel('High', fontsize=18)
ax.set_ylabel('Open', fontsize=16)
ax.set_zlabel('Close', fontsize=16)
# 绘制散点图
ax.scatter(X[:, 1], X[:, 0], X[:, 3], c= labels.astype(np.float))

多支股票单个字段聚类

数据获取

从维基百科中获取股票符号、行业和子行业。

# 美股
wiki_table = pd.read_html('https://en.wikipedia.org/wiki/List_of_S%26P_500_companies',header=0)[0]
symbols = list(wiki_table['Ticker symbol'])
# A股
import urllib
word = '深圳证券交易所主板上市公司列表'
word = urllib.parse.quote(word)
wiki_table = pd.read_html(f'https://zh.wikipedia.org/wiki/word',header=0)[0]
symbols = list(wiki_table['公司代码'])

或直接在深圳证券交易所下载A股列表。

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd 
import baostock as bs
# 从下载下来的A股列上获取上市公司名称及代码
zero = '000000'
A_table = pd.read_excel('./A股列表.xlsx')
A_codes = A_table['A股代码'].map(lambda x: zero[0: 6 - len(str(x))] + str(x))[0: 200].values
A_names = A_table['A股简称'][0: 200].values
print(A_codes)

['000001' '000002' '000004' '000005' '000006' '000007' '000008' '000009'
 '000010' '000011' '000012' '000014' '000016' '000017' '000019' '000020'
  ...
 '000611' '000612' '000613' '000615' '000616' '000617' '000619' '000620'
 '000622' '000623' '000625' '000626' '000627' '000628' '000629' '000630']

根据上面获得的股票代码下载相应日k线图。

bs.login()
dataset = pd.DataFrame()
for num, A_code in enumerate(A_codes):
    print(A_code)
    result = bs.query_history_k_data(A_code, fields = 'date,close',
                                    start_date = '2020-01-01',
                                    end_date = '2021-01-01',
                                    frequency='d')
    df_result = result.get_data().rename(columns='close':A_names[num])
    
    if num == 0:
        dataset = df_result
    else:
        dataset = dataset.merge(df_result, on=['date'])
bs.logout()
dataset = dataset.set_index('date').applymap(lambda x: float(x))

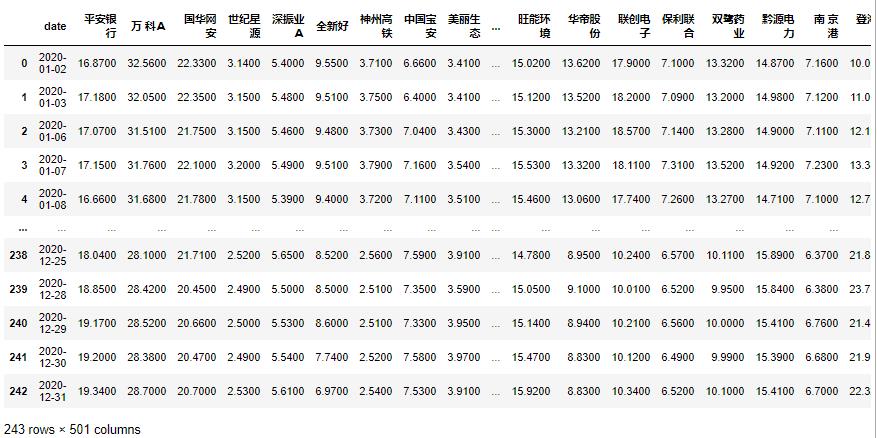
数据预处理

import math
# 计算一个理论一年的平均年收益率Returns和波动率Volatility
returns = dataset.pct_change().mean() * 252
returns = pd.DataFrame(returns)
# print(returns)
returns.columns = ['Returns']
returns['Volatility'] = dataset.pct_change(
                    ).std() * math.sqrt(252)
# print(returns['Volatility'])
# 将数据格式化为numpy数组以提供给K-Means算法
data = np.asarray(
          [np.asarray(returns['Returns']),
           np.asarray(returns['Volatility'])]
           ).T
# 删除NaN值，将其替换为0
cleaned_data = np.where(np.isnan(data), 0, data)
X = cleaned_data

建立聚类模型

from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler

# 在变量“n_clusters”中定义集群数量
n_clusters = 12

# 数据聚类
kmeans = KMeans(n_clusters)
kmeans.fit(X)

KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
    n_clusters=12, n_init=10, n_jobs=None, precompute_distances='auto',
    random_state=None, tol=0.0001, verbose=0)

绘制学习曲线

from sklearn.cluster import KMeans

min_clusters = 1
max_clusters = 20
distortions = []
for i in range(min_clusters, max_clusters+1):
    km = KMeans(n_clusters=i,
                init='k-means++',
                n_init=10,
                max_iter=300,
                random_state=0)
    km.fit(X)
    distortions.append(km.inertia_)
    
# 绘图
plt.figure(figsize=(14,6))
plt.plot(range(min_clusters, max_clusters+1), distortions, marker='o')
plt.xlabel("Number of clusters", fontsize=18)
plt.ylabel("Distortion", fontsize=16)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.show()

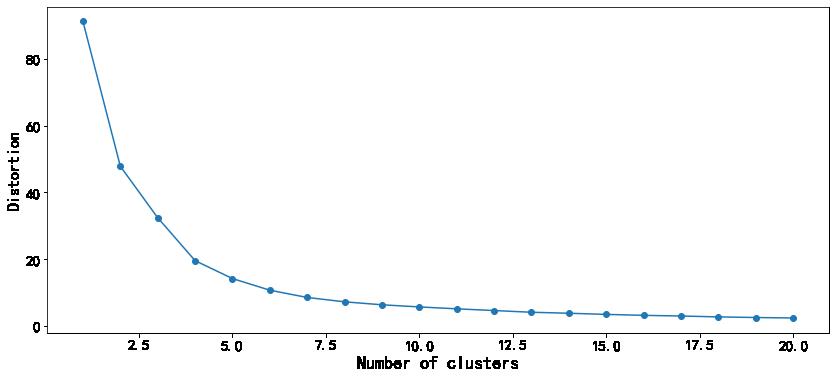
绘制轮廓系数

wcss = []
from sklearn.metrics import silhouette_score
for k in range(2, 20):
    k_means = KMeans(n_clusters=k)
    k_means.fit(X)
    wcss.append(silhouette_score(X, k_means.labels_))
fig = plt.figure(figsize=(15, 5))
plt.plot(range(2, 20), wcss)
plt.grid(True)
plt.xticks(fontsize=15)
plt.xlabel("Number of clusters", fontsize=18)
plt.ylabel('Silhouette_score', fontsize=15)
plt.title('Silhouette_score curve', fontsize=18)
plt.show()

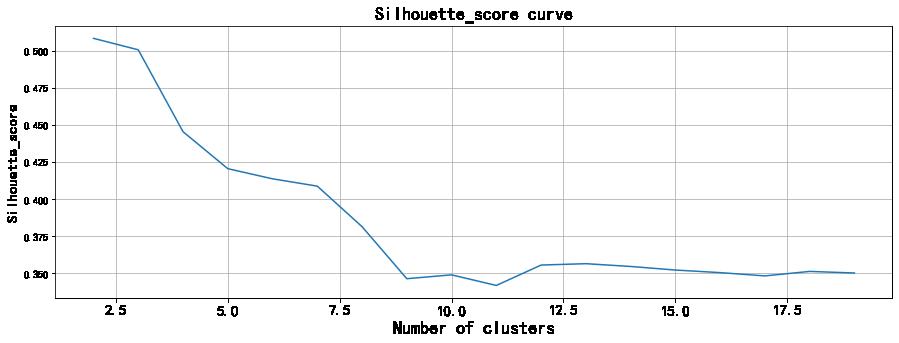
简单判断下，图中拐点位置大致在聚类中心个数为9时，此时轮廓系数最小。则n_clusters可以选择等于9.

scipy中的k-means

from scipy.cluster.vq import kmeans, vq
# 计算 K = 5 的K均值(5个簇)
centroids,_ = kmeans(cleaned_data,5)
# 将每个样本分配给一个簇
idx,_ = vq(cleaned_data,centroids)
data = cleaned_data

绘制聚类散点图

将每种簇按照不同的颜色区分绘制，同时绘制出簇中心。

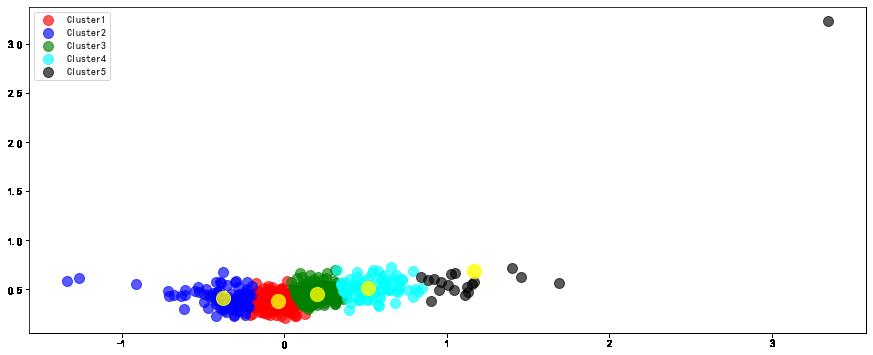
统计每个股票属于哪个簇

details = [(name,cluster) for name, 
          cluster in zip(returns.index,idx)]
labels =['A股简称', 'Cluster']
df = pd.DataFrame.from_records(details, 
                               columns=labels)
df.head(n=10)

|
| A股简称 | Cluster |
| — | — | — |
| 0 | 平安银行 | 3 |
| 1 | 万科Ａ | 1 |
| 2 | 国华网安 | 3 |
| 3 | 世纪星源 | 1 |
| 4 | 深振业Ａ | 3 |
| 5 | 全新好 | 2 |
| 6 | 神州高铁 | 2 |
| 7 | 中国宝安 | 3 |
| 8 | 美丽生态 | 3 |
| 9 | 深物业A | 0 |

多支股票多个字段举例

stocks_dict = dict(zip(A_names,A_codes))
bs.login()
dataset = []
for names, A_code in stocks_dict.items():
    print(A_code)
    result = bs.query_history_k_data(A_code, fields = 'date,open,high,low,close,volume',
                                    start_date = '2020-01-01',
                                    end_date = '2021-01-01',
                                    frequency='d')
    df_result = result.get_data()
    dataset.append(df_result)
bs.logout()

# 获取开盘价
open_price = np.array([p["open"] for p in dataset]).astype(np.float)

# 获取收盘价
close_price = np.array([p["close"] for p in dataset]).astype(np.float)
# 计算变化率
X = (close_price - open_price) / open_price

建模

from sklearn.cluster import KMeans
# 定义聚类中心个数
n_clusters = 12
kmeans = KMeans(n_clusters)
kmeans.fit(X)
# 输出结果
labels = kmeans.labels_
for i in range(n_clusters):
    print('Cluster %i: %s' % ((i + 1), 
          ', '.join(A_names[labels == i])))

使用管道链接归一化和聚类模型

from sklearn.pipeline import make_pipeline
from sklearn.cluster import KMeans
from sklearn.preprocessing import Normalizer

normalizer = Normalizer()
kmeans = KMeans(n_clusters=10, max_iter = 1000)
# 制作一个管道链接归一化和kmeans
pipeline = make_pipeline(normalizer, kmeans)
pipeline.fit(X)
labels = pipeline.predict(X)
df = pd.DataFrame('labels':labels,
                   'companies':A_names)
print(df.sort_values('labels'))

     labels companies
434       0      华铁股份
472       0      协鑫能科
419       0      首钢股份
417       0      中通客车
194       0      长安汽车
..      ...       ...
266       9      鲁  泰Ａ
268       9      国元证券
467       9      传化智联
234       9      中山公用
0         9      平安银行

[500 rows x 2 columns]

使用PCA降维

如果用于聚类的数据维度很高，在使用聚类分析时通常会占用过程的计算时间。此时运用PCAj降维方法。

from sklearn.preprocessing import Normalizer
from sklearn.decomposition import PCA
normalizer = Normalizer()
new_X = normalizer.fit_transform(X)
# 使用PCA降维
reduced_data = PCA(n_components = 2).fit_transform(new_X)
#对降维后的数据训练kmeans
kmeans = KMeans(n_clusters =10)
kmeans.fit(reduced_data)
labels = kmeans.predict(reduced_data)
# print(kmeans.inertia_)
# 创建DataFrame
df = pd.DataFrame('labels':labels,
                   'companies':A_names)
# 根据标签排序
print(df.sort_values('labels'))

3.2745576650179067
     labels companies
339       0      *ST长动
445       0      诚志股份
37        0      德赛电池
244       0      模塑科技
41        0      深 赛 格
..      ...       ...
275       9      南风化工
108       9      国际医学
22        9      深深房Ａ
444       9      九 芝 堂
164       9      *ST金洲

[500 rows x 2 columns]

可视化簇及簇中心

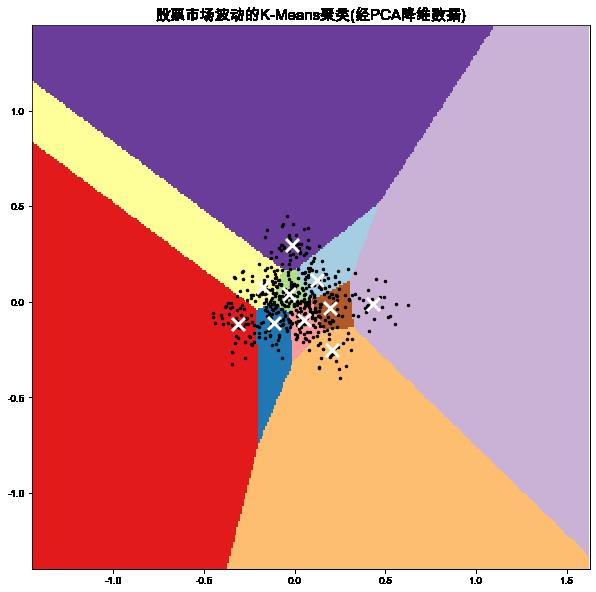
Min
以上是关于我总结了五种常用聚类分析算法，推荐收藏的主要内容，如果未能解决你的问题，请参考以下文章

资源|常用聚类算法学习推荐

聚类五种主要聚类算法

推荐｜数据科学家需要了解的5大聚类算法

空间聚类算法简述

基于K-Means聚类算法的主颜色提取

K-Means(K均值)GMM(高斯混合模型)，通俗易懂，先收藏了！