第三节：密度峰值聚类及其Python实现

Posted 2022-07-15 快乐江湖

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了第三节：密度峰值聚类及其Python实现相关的知识，希望对你有一定的参考价值。

文章目录

一：论文研读
二：算法思想
三：算法流程
四：Python实现
五：效果展示
六：算法优缺点

一：论文研读

2014年，Science上发表了一篇名为基于快速搜索和发现密度峰值的聚类方法，该算法能够自动发现簇中心，实现任意形状数据的高效聚类。所有这里有必要去研读一下这篇论文

Python代码

该算法思想：簇中心的密度比它们的邻居高，并且与高密度点的距离相对较大
该算法不管聚类的形状和嵌入的空间的维数如何，聚类都会被识别出来

关于簇的定义尚未达成共识，每种算法有各自的定义
重点讲了K-Means这类算法的缺点

重点说明了基于密度的DBSCAN算法的缺点

本文算法和K-medoids算法类似，它的基础仅是数据点之间的距离，和DBSCAN算法一样，它可以检测非凸数据也可以自动找到正确的簇类数目
本算法聚类中心被定义为数据点密度的局部极大值
本算法和mean-shift有所区别，并不要求在向量空间中嵌入数据并显示地最大化每个数据点的密度场

本算法基础：假设簇中心被局部密度较低的邻域包围，并且它们与任何局部密度较高的点之间的距离相对较大
每个点需要计算两个量：局部密 $p_i$ 和与高密度点的距离 $\\sigma_i$
一般来说， $p_i$ 等于比 $d_c$ 更接近点 $i$ 的点的数量，且对于大数据分析结果十分健硕的
$\\sigma_i$ 通过计算点 $i$ 和任何其他密度更高的点之间的最小距离来测量
聚类中心被认为是 $\\sigma$ 值异常大的点

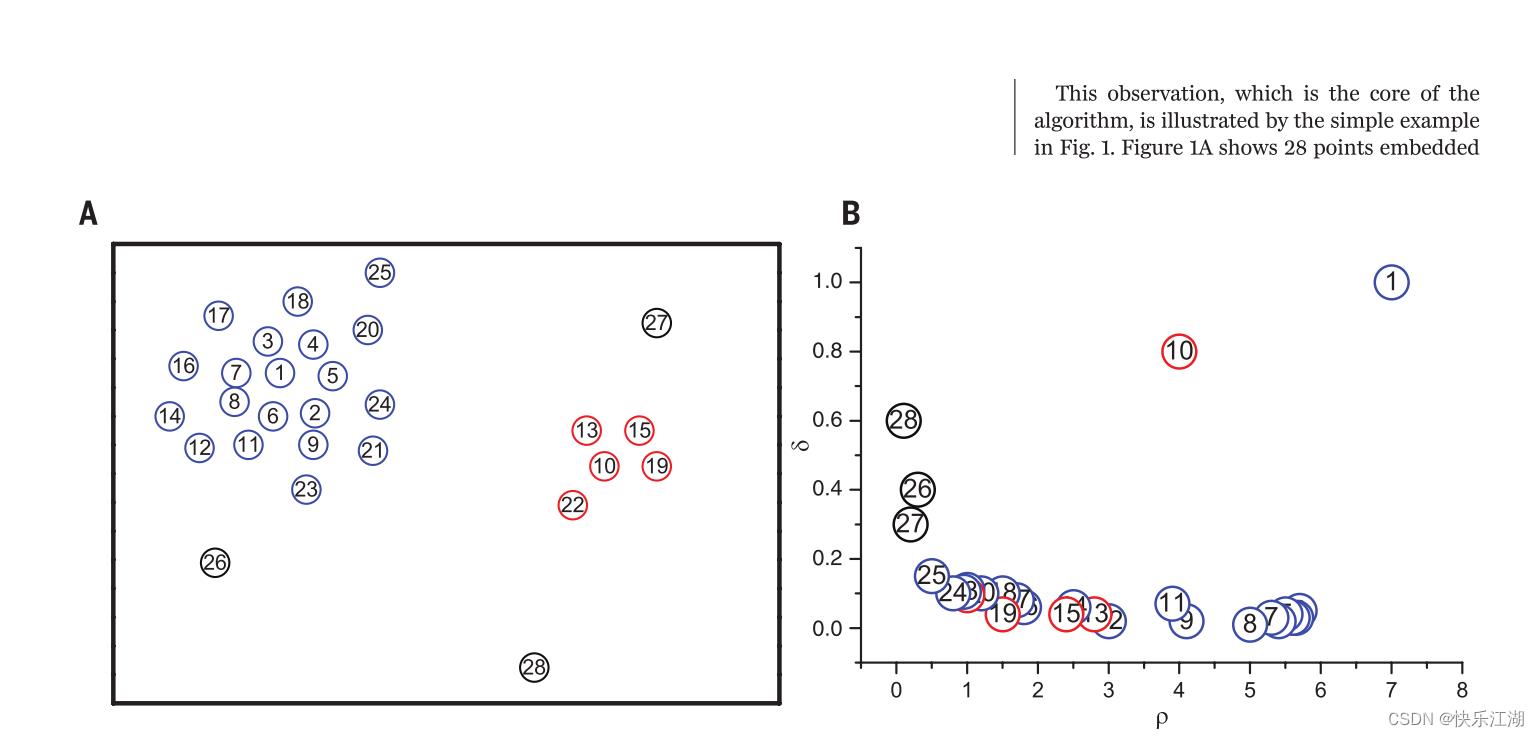
图1A展示的是二维空间中28个点，肉眼可见密度最大的便是1号点和10号点
图1B展示的是这28个点的 $p_i$ 和 $\\sigma_i$ 之间关系
本算法中这两张图称之为决策图
从图1B中可以看出，9号点和10号点 $p$ 值相同但 $\\sigma$ 不同：9号点处在1号点的簇中，其他有着高密度的点和其十分接近，然而10号点虽然和9号点密度相仿，但最近的高密度却属于其他簇（距离）
像点27、27、28由于 $p$ 很小、 $\\sigma$ 很大所以就是噪声点
聚类中心找到后，每个剩余的点被分配到同一个簇中，作为其密度较高的最近邻

然后，我们为每个簇找到一个边界区域，定义为分配给该簇但与属于簇的数据点的距离为 $d_c$ 的点集，接着为每个簇找到其边界区域内密度最高的点，用 $p_b$ 表示。之后，该簇中只要高于 $p_b$ 的点就会被考虑为核心点，其余点则适合作为噪声点

二：算法思想

（1）聚类中心的刻画

聚类算法有很多种，他们对聚类中心的描述也各有自己的特点。简单来说，本算法对聚类中心的刻画如下

自身的密度大，即它会被密度均不超过它的邻居包围——（即局部密度 $p_i$ ）
与其他密度更大的数据点之间的“距离”相对更大（即距离 $\\sigma_i$ ）

因此，考虑待聚类的数据集 $S=\\x_i\\^N_i=1$

$I_s=\\1, 2, 3, ... , N\\$ 为相应指标集
$d_ij=dist(x_i, x_j)$ 表示数据点 $x_i$ 和 $x_j$ 之间的某种距离
对于 $S$ 中的任何数据点 $x_i$ ，可以为其定义 $p_i$ 和 $\\sigma_i$ 用于刻画聚类中心

A：局部密度 $p_i$

①：使用Cut-of kernel计算，公式如下

该式表示的是： $S$ 中与 $x_i$ 之间距离小于 $d_c$ 的数据点的个数（不考虑 $x_i$ 本身）
参数 $d_c>0$ 表示 截断距离，需要用户事先指定
注意Cut-of kernel是 离散值

$p_i=\\sum_j\\chi(d_ij-d_c)$

其中函数
$\\chi(x)=\\begincases 1，x < 0\\\\ 0，x \\geq 0 \\endcases$

对于 $d_c$ 的确定，文章指出：As a rule of thumb, one can choose $d_c$ so that the average number of neighbors is around 1 to 2% of the total number of points in the data set（选取一个 $d_c$ ，使得每个数据点的平均邻居个数为数据点总数的1%~2%，这里的邻居是指与之距离不超过 $d_c$ 的数据点）