【统计与检验-3】p-value,q-value and FDR

Posted 2023-04-01

参考技术A 最近数据分析，涉及到了fdr的筛选，参考文章时，文章中选择了fdr 0.1作为cutoff，但是数据离谱，0.1 作为阈值对于我的数据毫无意义，一个significant 的基因都没有。这时候我们就开始讨论是否可以提高cutoff，这样做是否正确，多大时能够使用，最后我们开始想是否可以用p-value 进行筛选，于是我们开始对这些概念进行讨论，到底什么是p-value,fdr和qvalue,怎么计算得到。参考各种资料，和实验室大牛的讨论。慢慢的开始有了模糊理解，这里写写自己的理解，方便以后自己忘记的时候，查阅。
p-value:p-value是在假设检验中产生出来的概念，比如t-test,f-test,z-test等检验方法都会产生p-value 值。(我还记得年轻时提出了和别人讨论了一个问题，这些pvalue是不是都是一个概念。其实他们周围的人都说不是一个概念，但是我想说的是其实它就是一个概念) 。如图所示，p-value表示支持原假设的程度，取值范围是［0-1］，值越大，说明原假设成立的可能性越高，当它足够小时，我们认为原假设不成立，比如0.01，亦或者是0.05。

线性回归--假设检验（F统计量P-value）

 一、F检验解释

 F检验（F-test），最常用的别名叫做联合假设检验（英语：joint hypotheses test），此外也称方差比率检验、方差齐性检验。它是一种在原假设（null hypothesis, H0）之下，统计值服从F-分布的检验。

二、线性回归基础：

通常对于一组特征数据和其标记值：(x1,y1)，(x2,y2)......(xn,yn)在使用特征值对进行预测时，根据习惯，如果是连续的，则称这种操作或者技术为回归；如果是离散的，则通常称为分类。 

线性回归模型可以描述为：。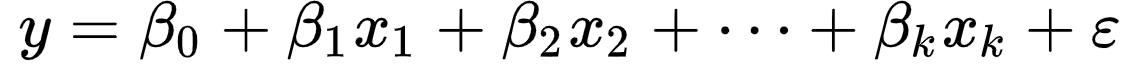

 三、模型假设检验：

H0 :β1 =β2 =...=βk =0。

H1: 至少有一个 βi 不等于 0, i = 1,2,...,k。

Test statistics, F0 =（SSR/k）/ [SSE/(n-k-1)] ∼ F(k,n − k − 1)。

拒绝H0假设的条件α,如果|F|>F(1−α,1,n−k-1)。

四、举例：

根据数值SST = 3650.8，SSR = 1755.9，n=15，k =1，α = 0.05，求统计量F，判断是否可以拒绝0假设。

F0 = （SSR/k）/ [SSE/(n-k-1)] =  = [(1755.9) / 1] / [(3650.8 - 1755.9) / (15 - 1- 1)] = 12.04

查表得到Fc = 4.667

F0 > Fc,拒绝假设

p-value < α,拒绝假设