Tree-LSTM的一些理解以及DGL代码实现

Posted 2022-07-12 Icy Hunter

文章目录

• 前言
• Tree-LSTM
• • LSTM
  • N-ary Tree-LSTM
  • Child-sum Tree-LSTM
• DGL代码实现
• • N-ary Tree-LSTM
  • Child-sum Tree-LSTM
• 参考

前言

Tree-LSTM其实在好久之前就研究过了，那也应该是我第一次学DGL的时候。因为树就是一种特殊的图，也算是我入门图神经网络的基础操作，依稀记得当时搞着模型也是弄了蛮久的…

Tree-LSTM

Tree-LSTM是一种树形结构的LSTM，能够提高LSTM计算的并行速度，同时能够融入依存树或者句法树的相关信息，从而达到比较好的句子建模的效果。

Tree-LSTM有两种形式，一种是N-ary Tree-LSTM还有一种是Child-sum Tree-LSTM，前者能够记录时序信息但对孩子节点的个数有特点限制，后者会失去位置信息，但是对孩子节点的个数没有要求。

LSTM

在理解两种Tree-LSTM前，可以回顾一下我们经典的LSTM:

其中：
σ（）、tanh（）是激活函数
i_t是输入们得到的信息，x^t 是输入的特征，W⁽ⁱ⁾ 是对应输入门输入特征的变换矩阵，h_t-1是前一个状态的隐藏层 U⁽ⁱ⁾ 是输入门隐藏层的变换矩阵，b⁽ⁱ⁾ 为输入门的偏置

f_t是遗忘门得到的信息，x^t 是输入的特征，W^(f) 是对应遗忘门输入特征的变换矩阵，h_t-1是前一个状态的隐藏层 U^(f) 是遗忘门隐藏层的变换矩阵，b^(f) 为遗忘门的偏置

o_t是输出门得到的信息，x^t 是输入的特征，W^(o) 是对应输出门输入特征的变换矩阵，h_t-1是前一个状态的隐藏层 U^(o) 是输出门隐藏层的变换矩阵，b^(o) 为遗忘门的偏置

c_t为当前的细胞状态，⨀代表点积，即矩阵对应元素相乘

h_t则是更新后的隐藏层

总的来说，公式还是比较简单的，因为没有Σ求和符号什么的，读懂公式的计算过程还是很容易的。

N-ary Tree-LSTM

N-ary Tree-LSTM即有N个孩子节点的Tree-LSTM，特点是能够较好的保留时序信息，不过对孩子节点的个数有限制要求，因此这种一般都为二叉树结构的输入，因为计算起来比较简单。

N-ary Tree-LSTM和经典的LSTM就是多了几个Σ求和符号。

如果N=2，那么意味着每个父节点的孩子节点数都为2，那么输入门、输出门、遗忘门中各自有两个U来对前一时刻对应两个孩子节点的隐藏层进行线性变换，然后求和，因为这操作分别对应左右两个孩子，因此是能够记录时序信息的。因为N=2是事先设定的，如果你的数据里出现了三个孩子节点的情况，那么就要报错了。

还是举个例子比较形象

例如N=2，0为父节点，那么N-ary Tree-LSTM会在子节点1和2的位置中的三种门中分别设置一个隐藏层变换矩阵U1和U2，左节点就和U1计算，右节点就和U2计算，这样就保证位置信息能够得以保留，但是不能够解决数据中含有三叉及以上的情况。

Child-sum Tree-LSTM

Child-sum Tree-LSTM就比较简单了，顾名思义，他就是将子节点的隐藏层都求和然后再去更新父节点的隐藏层。

对比N-ary Tree-LSTM可以发现三个门中的Σ求和符号没了，因为（2）中将孩子节点的隐藏层直接求和，记为$\tilde{h}$_j，然后用它进去三门进行计算即可。因为这里是求和操作，那么孩子节点的个数就不受限制了，因为求和之后就相当于只有一个了，三门中只需要设置一个对应的U即可，但是缺点就是，求和之后，孩子节点的位置信息就失去了。

以及这里遗忘门是对每个孩子节点各自求一个遗忘信息，不过是共享参数U^(f)

同样可以举个例子，例如此时N=3
如果是N-ary Tree-LSTM:

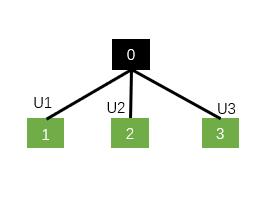
就要对应分别三组。
如果是Child-sum Tree-LSTM:

只需要一个就可以了，因为子节点都求和了。

DGL代码实现

N-ary Tree-LSTM

这个代码完全来自DGL官网。这里是一个对每个节点做预测的情感分类任务。

from collections import namedtuple

import dgl
from dgl.data.tree import SSTDataset


SSTBatch = namedtuple('SSTBatch', ['graph', 'mask', 'wordid', 'label'])

# Each sample in the dataset is a constituency tree. The leaf nodes
# represent words. The word is an int value stored in the "x" field.
# The non-leaf nodes have a special word PAD_WORD. The sentiment
# label is stored in the "y" feature field.
trainset = SSTDataset(mode='tiny')  # the "tiny" set has only five trees
tiny_sst = trainset.trees
num_vocabs = trainset.num_vocabs
num_classes = trainset.num_classes

vocab = trainset.vocab # vocabulary dict: key -> id
inv_vocab = v: k for k, v in vocab.items() # inverted vocabulary dict: id -> word

a_tree = tiny_sst[0]
for token in a_tree.ndata['x'].tolist():
    if token != trainset.PAD_WORD:
        print(inv_vocab[token], end=" ")

import torch as th
import torch.nn as nn

class TreeLSTMCell(nn.Module):
    def __init__(self, x_size, h_size):
        super(TreeLSTMCell, self).__init__()
        self.W_iou = nn.Linear(x_size, 3 * h_size, bias=False)
        self.U_iou = nn.Linear(2 * h_size, 3 * h_size, bias=False)
        self.b_iou = nn.Parameter(th.zeros(1, 3 * h_size))
        self.U_f = nn.Linear(2 * h_size, 2 * h_size)

    def message_func(self, edges):
        return 'h': edges.src['h'], 'c': edges.src['c']

    def reduce_func(self, nodes):
        # concatenate h_jl for equation (1), (2), (3), (4)
        h_cat = nodes.mailbox['h'].view(nodes.mailbox['h'].size(0), -1)
        # equation (2)
        f = th.sigmoid(self.U_f(h_cat)).view(*nodes.mailbox['h'].size())
        # second term of equation (5)
        c = th.sum(f * nodes.mailbox['c'], 1)
        return 'iou': self.U_iou(h_cat), 'c': c

    def apply_node_func(self, nodes):
        # equation (1), (3), (4)
        iou = nodes.data['iou'] + self.b_iou
        i, o, u = th.chunk(iou, 3, 1)
        i, o, u = th.sigmoid(i), th.sigmoid(o), th.tanh(u)
        # equation (5)
        c = i * u + nodes.data['c']
        # equation (6)
        h = o * th.tanh(c)
        return 'h' : h, 'c' : c


class TreeLSTM(nn.Module):
    def __init__(self,
                 num_vocabs,
                 x_size,
                 h_size,
                 num_classes,
                 dropout,
                 pretrained_emb=None):
        super(TreeLSTM, self).__init__()
        self.x_size = x_size
        self.embedding = nn.Embedding(num_vocabs, x_size)
        if pretrained_emb is not None:
            print('Using glove')
            self.embedding.weight.data.copy_(pretrained_emb)
            self.embedding.weight.requires_grad = True
        self.dropout = nn.Dropout(dropout)
        self.linear = nn.Linear(h_size, num_classes)
        self.cell = TreeLSTMCell(x_size, h_size)

    def forward(self, batch, h, c):
        """Compute tree-lstm prediction given a batch.

        Parameters
        ----------
        batch : dgl.data.SSTBatch
            The data batch.
        h : Tensor
            Initial hidden state.
        c : Tensor
            Initial cell state.

        Returns
        -------
        logits : Tensor
            The prediction of each node.
        """
        g = batch.graph
        # to heterogenous graph
        g = dgl.graph(g.edges())
        # feed embedding
        embeds = self.embedding(batch.wordid * batch.mask)
        g.ndata['iou'] = self.cell.W_iou(self.dropout(embeds)) * batch.mask.float().unsqueeze(-1)
        g.ndata['h'] = h
        g.ndata['c'] = c
        # propagate
        dgl.prop_nodes_topo(g,
                            message_func=self.cell.message_func,
                            reduce_func=self.cell.reduce_func,
                            apply_node_func=self.cell.apply_node_func)
        # compute logits
        h = self.dropout(g.ndata.pop('h'))
        logits = self.linear(h)
        return logits


from torch.utils.data import DataLoader
import torch.nn.functional as F

device = th.device('cpu')
# hyper parameters
x_size = 256
h_size = 256
dropout = 0.5
lr = 0.05
weight_decay = 1e-4
epochs = 10

# create the model
model = TreeLSTM(trainset.num_vocabs,
                 x_size,
                 h_size,
                 trainset.num_classes,
                 dropout)
print(model)

# create the optimizer
optimizer = th.optim.Adagrad(model.parameters(),
                          lr=lr,
                          weight_decay=weight_decay)

def batcher(dev):
    def batcher_dev(batch):
        batch_trees = dgl.batch(batch)
        return SSTBatch(graph=batch_trees,
                        mask=batch_trees.ndata['mask'].to(device),
                        wordid=batch_trees.ndata['x'].to(device),
                        label=batch_trees.ndata['y'].to(device))
    return batcher_dev

train_loader = DataLoader(dataset=tiny_sst,
                          batch_size=5,
                          collate_fn=batcher(device),
                          shuffle=False,
                          num_workers=0)

# training loop
for epoch in range(epochs):
    for step, batch in enumerate(train_loader):
        g = batch.graph
        n = g.number_of_nodes()
        h = th.zeros((n, h_size))
        c = th.zeros((n, h_size))
        logits = model(batch, h, c)
        logp = F.log_softmax(logits, 1)
        loss = F.nll_loss(logp, batch.label, reduction='sum')
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        pred = th.argmax(logits, 1)
        acc = float(th.sum(th.eq(batch.label, pred))) / len(batch.label)
        print("Epoch :05d | Step :05d | Loss :.4f | Acc :.4f |".format(
            epoch, step, loss.item(), acc))

Child-sum Tree-LSTM

可以看懂了N-ary再来看Child-sum的，差不太多。

import torch as th
import torch.nn as nn
class ChildSumTreeLSTMCell(nn.Module):
    def __init__(self, x_size, h_size):
        super(ChildSumTreeLSTMCell, self).__init__()
        self.W_iou = nn.Linear(x_size, 3 * h_size, bias=False)
        self.U_iou = nn.Linear(h_size, 3 * h_size, bias=False)
        self.b_iou = nn.Parameter(th.zeros(1, 3 * h_size))
        self.U_f = nn.Linear(h_size, h_size)

    def message_func(self, edges):
        return 'h': edges.src['h'], 'c': edges.src['c']

    def reduce_func(self, nodes):
        h_tild = th.sum(nodes.mailbox['h'], 1)
        f = th.sigmoid(self.U_f(nodes.mailbox['h']))
        c = th.sum(f * nodes.mailbox['c'], 1)
        return 'iou': self.U_iou(h_tild), 'c': c

    def apply_node_func(self, nodes):
        iou = nodes.data['iou'] + self.b_iou
        i, o, u = th.chunk(iou, 3, 1)
        i, o, u = th.sigmoid(i), th.sigmoid(o), th.tanh(u)
        c = i * u + nodes.data['c']
        h = o * th.tanh(c)
        return 'h': h, 'c': c



class TreeLSTM(nn.Module):
    def __init__(self,
                 num_vocabs,
                 x_size,
                 h_size,
                 num_classes,
                 dropout,
                 pretrained_emb=None):
        super(TreeLSTM, self).__init__()
        self.x_size = x_size
        self.embedding = nn.Embedding(num_vocabs, x_size)
        if pretrained_emb is not None:#这里可以使用预训练词向量
            print('Using glove')
            self.embedding.weight.data.copy_(pretrained_emb)
            self.embedding.weight.requires_grad = True
        self.dropout = nn.Dropout(dropout)
        self.linear = nn.Linear(h_size, num_classes)
        self.cell = ChildSumTreeLSTMCell(x_size, h_size)

    def forward(self, batch, h, c):
        """Compute tree-lstm prediction given a batch.

        Parameters
        ----------
        batch : dgl.data.SSTBatch
            The data batch.
        h : Tensor
            Initial hidden state.
        c : Tensor
            Initial cell state.

        Returns
        -------
        logits : Tensor
            The prediction of each node.
        """
        # print("batch", batch)
        g = batch.graph
        # print("g", g)
        # to heterogenous graph
        g = dgl.graph(g.edges())
        # feed embedding
        embeds = self.embedding(batch.wordid * batch.mask)
        #叶子节点没有入度，因此message_func和reduce_func都可以忽略，直接apply_node_func

        g.ndata['iou'] = self.cell.W_iou(self.dropout(embeds)) * batch.mask.float().unsqueeze(-1)
        g.ndata['h'] = h
        g.ndata['c'] = c
        g.ndata['node_pos'] = batch.node_pos
        # print(type(batch.wordid))
        # prop_nodes_topo是根据我们指定的拓扑顺序来进行消息传递
        dgl.prop_nodes_topo(g,
                            message_func=self.cell.message_func,
                            reduce_func=self.cell.reduce_func,
                            apply_node_func=self.cell.apply_node_func)
        # compute logits
        # print("after_prop_nodes_topo", g)
        h = self.dropout(g.ndata.pop('h'))
        pos = g.ndata["node_pos"]
        pos_sen = torch.nonzero(pos==0).squeeze()  # 0的位置为根节点
        sen_hidden = h[pos_sen]

        logits = self.linear(sen_hidden)
        return logits

child_sum_Tree_LSTM = TreeLSTM(100, 50, 50, 2, 0.2)
print(child_sum_Tree_LSTM)

参考

2015-Tree-LSTM-Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks
https://docs.dgl.ai/tutorials/models/2_small_graph/3_tree-lstm.html#sphx-glr-tutorials-models-2-small-graph-3-tree-lstm-py