Java解决约瑟夫环问题（通俗易懂版）

Posted 2023-04-01 LCW0102

约瑟夫环问题：
         约瑟夫环(约瑟夫问题)是一个数学的应用问题:已知n个人(以编号1，2，3…n分别表示)围坐在一张圆桌周围。从编号为k的人开始报数，数到m的那个人出列;他的下一个人又从1开始报数，数到m的那个人又出列;依此规律重复下去，直到圆桌周围的人全部出列。通常解决这类问题时我们把编号从0~n-1，最后 结果+1即为原问题的解。
解法一：利用链表
         我们可以把每一个人变成一个链表，然后不断地循环这个链表。每次删除一个结点，直到最终只剩下一个结点的时候就表示我们找到个！

	//设计一个结点类
	class Node
        int val;
        Node next;
        public Node(int val)
            this.val = val;
        
    
    /**
     * 循环链表
     * @param n 一共有n个人（每个人的编号从0开始到-1）
     * @param m 每次出去第m个人（每次报数也是从0开始到m-1）
     * @return
     */
    public int LastRemaining_Solution3(int n, int m) 
    	//这里表示没有人的情况
        if(n == 0 || m == 0)
            return -1;
        
        //创建一个头结点（将第一个人设置为头）
        Node head = new Node(0);
        //把头结点保存一妇女进行循环~
        Node temp = head;
        //然后我们从第二个人开始，不穿创建结点并和之前的节点进行连接
        for(int i = 1 ; i < n ; i++)
            temp.next = new Node(i);
            temp = temp.next;
        
        //让最后一个人和我们的第一个人也连在一起，这样就可以循环起来了~
        temp.next = head;
        //因为我们设计的是从0开始
        int index = 0;
        //当链表不止一个结点的时候才需要循环了
        while(head.next != head)
        	//这里还是我们停在需要删除的节点的前一个
            if(index == m-2)
            	//删除该节点
                head.next = head.next.next;
                //同时我们的报数需要清0，重新开始报数
                index = 0;
            
            //如果不是要删除的节点那就正常报数
            else
                index++;
            
            //每次向后移动一个
            head = head.next;
        
        //最终返回剩下的那一个节点的值就好啦~
        return head.val;
    

解法二：迭代
         我们先举个例子~假设一共有5个人（n = 5），然后从0开始编号，从0开始报数，报到第2个出列（m = 3），我们来模拟一下这个过程。

0 1 2 3 4 （第一次出队的是2）
3 4 0 1 （第二次出队的是0）
1 3 4 （第三次出队的是4）
1 3 [ 1 3 ]（第四次出队的是1）
3（最终剩余的是3）

         我们做这个题的时候只知道最后剩下的一定是一个数，他的下标是0，那我们可以从下往上看，根据下标找到最终的那个数。
         所以我们需要看怎么从下面这一层的下标找到这个数在上一层的下标，我们发现当前下标加上m就是我们再上一层的下标，但是这个不一定是真实的下标，因为有可能我们当前的人数是小于m的，所以得到的下标就是一个将人数复制了之后的下标，那么想要得到真实的下标就是进行一个%操作就好，我们知道每次只出队1 个人，那么从后往前的人数分别是0，1，2…所以我们%一下这个人数就得到了真实的下标，然后再一样的办法，得到上一次循环该数的下标，直到到了最开始就知道我们这个最终剩下的人的下标，因为我们最开始的编号是从0开始的，所以回到最初的时候，下标就是编号，直接返回就好了！

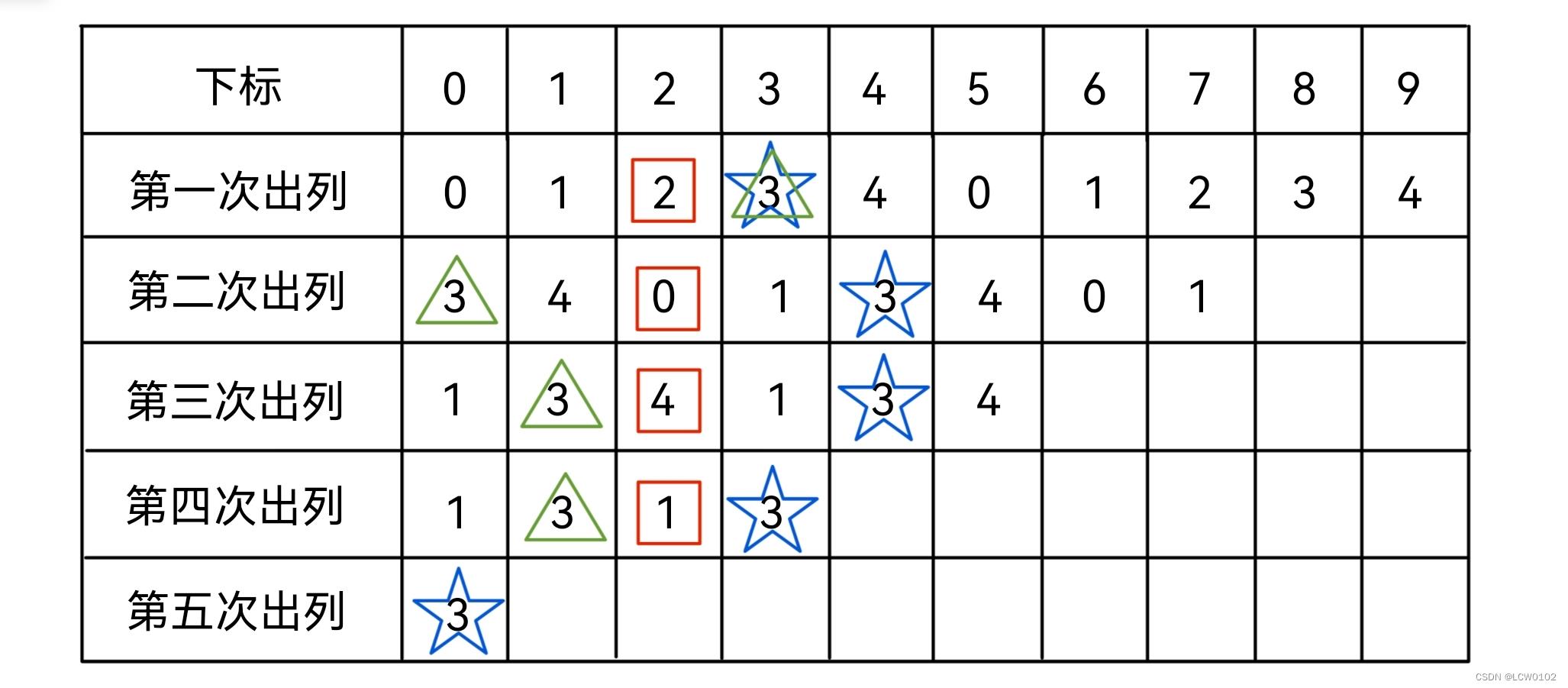
         我们看这个图，红色的是每次要删除的数据，蓝色的是我们的到的下标，绿色的是真实的下标。我们最开始只知道最后一个3的下标是0，然后不断往上一层找，拿到3的下标。
代码：

	public int LastRemaining_Solution(int n, int m) 
		//先判断没有人的状况
        if(n == 0 || m == 0)
            return -1;
        
        //我们知道最后的下标是0
        int index = 0;
        //从下往上找最初的下标
        for(int i = 2 ; i <= n ; i++)
        	//当前下标加上m是蓝色的那个下标
        	//再模一下当前的人数就是真实的下标~
            index = (index + m) % i;
        
        //最终直接返回下标~
        return index;
    

还有的时候我们的是从1开始编号报数的，那么具体的代码是

public int LastRemaining_Solution2(int n, int m) 
        if(n == 0 || m == 0)
            return -1;
        
        int index = 1;
        for(int i = 2 ; i <= n ; i++)
            index = (index + m) % i;
            if(index == 0)
                index += i;
            
        
        return index;
    

         会比0开始的多一个步骤，但是思路完全一样~

约瑟夫环的java解决

总共3中解决方法，1、数学推导，2、使用ArrayList递归解决，3、使用首位相连的LinkedList解决

import java.util.ArrayList;

/**
* 约瑟夫环问题
* 需求：n个人围成一圈，从第一个人开始报数，数到K的人出局，然后从下一个人接着报数，直到最后一个人，求最后一个人的编号
* @author Miao
*
*/
public class Josephus {
public static void main(String[] args) {
int n = 13;
int k = 3;
int last;
// last =getLast(n,k); //使用数学推导求结果
/* 使用递归求结果
* ArrayList<Integer> list = new ArrayList<Integer>();
for (int i = 1; i <= n; i++) {
list.add(i);
}
last = getLast(list, k,0); //从下标为0开始报数，
*/
// System.out.println(last);
/**
* 使用链表方式求结果，链表为头尾相接的环形链表
*/

MyLinkedList list = new MyLinkedList();
for (int i = 1; i <= n; i++) {
list.add(i);
}
//只要链表中元素个数大于1个，则指向下面步骤
while(list.length>1){
Node temp = list.first; //获得头节点
//将temp节点从头节点向后挪k个位置
for (int i = 1; i < k; i++) {
temp = temp.next;
}

System.out.println("被移除的编号为："+temp.value);
list.remove(temp); //移除当前temp位置的节点
System.out.println("剩余元素为："+list.toString()+",长度为"+list.length);
}
//当上面循环结束时，链表内只剩1个元素
last = list.first.value;
System.out.println(last);
}
/**
* 数学推导，已知圈内只有一个人时候，剩余的是编号1，根据推导，如果当圈内有n-1个人时剩余的人编号为last，
* 那么当圈内有n人时，剩余的人的编号是last+k，因为可能last+k以后大于了当前圈内人数，所以剩余的
* 人的编号为(last+k)%n，但这时就会出现如果last+k后指向最后一个人，这时得到的编号为0，不符合要
* 求，所以用((last+k-1)%n)+1，这样最后一个人报的数也是自己了，而其他位置的人报数不变。
*
* @param n 圈内人数
* @param k 数到该数字的人出局
* @return 剩余人的编号
*/
public static int getLast(int n , int k){

int last = 1; //这是初始值，即环内为1个人时剩余的人的编号，必然为1，也是后面推导的基础
//System.out.println("当环内有1个人时，剩余的是:1");
for (int i = 2; i <= n; i++) { //当圈内为i个人时，结果是圈内为i-1个人的结果加K后对i求余
last = ((last + k - 1) % i) + 1; //为避免出现结果为0，让i-1的结果先减1，求余后再加1
//System.out.println("当环内有" + i + "个人时，剩余的是:" + last);
}
return last;
}

/**
* 递归方式：第一轮根据传入的集合、开始下标和间隔求出第一轮出局的人的下标，然后将该人移出集合，
* 并求出下一轮的开始下标，然后迭代调用本方法，将剩余集合元素和新的开始下标传入计算，
* 直至剩余最后一个元素，就是最后存货的元素
* @param list 传入的集合
* @param k 报数到K的人出局
* @param m 从下标为m的人开始报数
* @return 剩余最后一个人的编号
*/
public static int getLast(ArrayList<Integer> list, int k , int m){
int last = -1; //用来放置最后一个人的编号
int index = -1; //用来放置当前一轮被移除的人的下标
if (list.size() == 1) { // 如果集合内只剩一个元素，则直接返回该元素作为结果
last = list.get(0);
} else {
index = (m + k - 1) % list.size(); // 求出当前一轮被移除的人的下标
/* System.out.println("当前集合内的元素为：" + list.toString());
System.out.println("从" + list.get(m) + "开始报数,被移除的是:"
+ list.get(index));*/
list.remove(index); // 将该人移除
m = index % list.size(); // 求出新一轮报数时开始的人在新集合里的下标
last = getLast(list, k, m); // 使用剩余的集合和m的位置重新开始下一轮计算
}
return last;
}

}

/**
* 定义一个双向节点类，用作实现链表功能
* @author Miao
*
*/
class Node{
Integer value;
Node next;
Node prev;
public Node(){
value = null;
prev=null;
next = null;
}
public Node(Integer value){
this.value = value;
next = null;
prev = null;
}
public String toString(){
return this.prev.value+"<"+this.value+">"+this.next.value;
}
}
/**
* 定义自己的双向链表类，用来放置数据
* @author Miao
*
*/
class MyLinkedList{
public Node first;
public Node last;
public int length;
public MyLinkedList(){
first = new Node();
last = first;
length = 0;
}
//在链表结尾增加元素的方法
public void add(Integer i){
if(length == 0){
first.value = i; //添加第一个元素，只需要设置该元素的value
}else{
Node temp = new Node(); //添加元素时，1、新建一个元素，
temp.value = i;
temp.prev = last; //2、然后先与last节点建立双向关系，
last.next = temp;
first.prev = temp; //3、再与first节点建立双向关系，
temp.next = first;
last = temp; //4、最后让last指向该节点，3、4步可颠倒
}

length++;
}
//从链表中删除指定节点的方法
public void remove(Node node){
node.prev.next = node.next; //将前节点的next跳过本节点，指向下个节点
node.next.prev = node.prev; //将后节点的prev跳过本节点，指向前节点 ，此时该节点已经从链表中移除了
this.first = node.next; //指定后节点为头节点
this.last = node.prev; //指定前节点为尾节点
node = null;
length--;
}

public String toString(){
String str ="[";
Node temp = first;
for (int i = 1 ; i < length; i++ ) {
str += temp.value+",";
temp = temp.next;
}
str += (temp.value+"]");
return str;
}


}