高等数学——二重积分

Posted 2023-04-01 超级种码

文章目录

• 版权声明
• 概念
• 性质
• 计算
• • 利用直角坐标计算
  • 利用极坐标计算
  • 利用函数的奇偶性计算
  • 利用变量的轮换对称性计算

版权声明

本文大部分内容皆来自武忠祥老师考研教材和视频课。

概念

• 定义：设函数$z=f(x,y)$在有界区域$D$上有定义，将区域$D$任意分成$n$个小区域$\Delta {\sigma }_1,\Delta {\sigma }_2,...,\Delta {\sigma }_n$，其中$\Delta {\sigma }_i$代表第$i$个小区域，也表示它的面积，在每个$\Delta {\sigma }_i$上任取一点$({\xi }_i,{\eta }_i)$，做乘积$f({\xi }_i,{\eta }_i)\Delta {\sigma }_i$，并求和${\sum }_{i=1}^{n}f({\xi }_i,{\eta }_i)\Delta {\sigma }_i$，记$\lambda$为$n$个小区域$\Delta {\sigma }_1,\Delta {\sigma }_2,...,\Delta {\sigma }_n$中最大直径，如果${\sum }_{i=1}^{n}f({\xi }_i,{\eta }_i)\Delta {\sigma }_i$存在，则称$f(x,y)$在区域$D$上的二重积分，记为${\iint }_{D}f(x,y)d\sigma =\underset{\lambda \to 0}{\lim }{\sum }_{i=1}^{n}f({\xi }_i,{\eta }_i)\Delta {\sigma }_i$。
• 几何意义：二重积分${\iint }_{D}f(x,y)d\sigma$是一个数，当$f(x,y)\ge 0$时，其值等于以区域$D$为底，以曲面$z=f(x,y)$为曲顶柱体的体积，当$f(x,y)\le 0$时，二重积分的值为负数，其绝对值等于上述曲顶柱体的体积。

性质

• 不等式性质：
  • 若在$D$上$f(x,y)\le g(x,y)$，则${\iint }_{D}f(x,y)d\sigma \le {\iint }_{D}g(x,y)d\sigma$；
  • 若在$D$上$m\le f(x,y)\le M$，则$m\sigma \le {\iint }_{D}f(x,y)d\sigma \le M\sigma$（其中$\sigma$为区域$D$的面积）；
  • $|{\iint }_{D}f(x,y)d\sigma |\le {\iint }_D|f(x,y)|d\sigma$。
• 中值定理：设函数$f(x,y)$在闭区域$D$上连续，$\sigma$为区域$D$的面积，则在$D$上至少存在一点$(\xi ,\eta )$，使得${\iint }_{D}f(x,y)d\sigma =f(\xi ,\eta )\sigma$。

计算

利用直角坐标计算

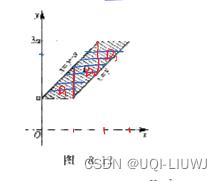
• 先$y$后$x$，积分区域$D$可以用$a\le x\le b$， φ 1 ( x ) ≤ y ≤ φ 2 ( x ) \\varphi_1(x)≤y≤\\varphi_2(x) φ1​(x)≤y≤φ

  数学知识整理：二重积分

  1 二重积分的性质

  1.1 f(x,y)在有界闭区域上可积的充分条件&必要条件

  • 在有界闭区域D上可积的函数f(x,y)必然是D上的有界函数
  • 有界闭区域D上的连续函数或者分片连续函数f(x,y)在D上可积

  1.2 线性性质

  

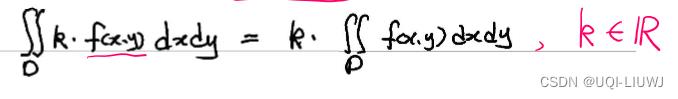
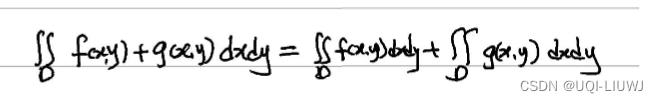
  1.3 积分区域可加

  （换言之，区域D被一条曲线分成两个部分区域D1和D2）

  1.4 积分不等式

  

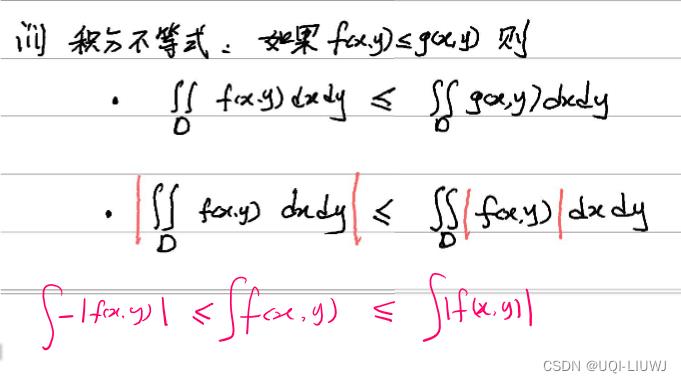
  1.5 中值定理

  如果函数f(x,y)在有界闭区域D上连续，那么在D上至少存在一点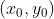，使得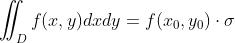，其中σ为区域D的面积

  2 二重积分的计算方法

  二重积分的计算总是化成累次积分来进行，也就是做一次定积分，再做一次定积分来进行计算。

  

   

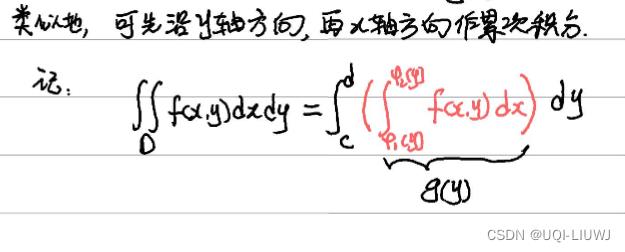
  2.1 按区域和形状分类

   

  2.2 二重积分简化计算

  • 当区域D关于x轴对称时
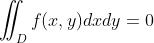    • · ,f(x,y)是奇函数
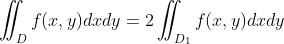    • ，f(x,y)是偶函数，且D1是D的上半平面或者下半平面
  • 当区域D关于y轴对称时
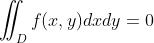    • · ,f(x,y)是奇函数
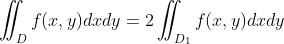    • ，f(x,y)是偶函数，且D1是D的左半平面或者右半平面
  • 当区域D关于x轴，y轴都对称时
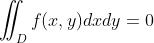    •  · ,f(x,y)是奇函数
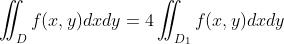    • ，f(x,y)是偶函数，且D1是D在任一象限中的部分

  1.2.3 举例

  

   

   

  3 二重积分<——>极坐标二重积分

  

  

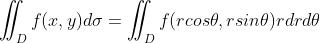
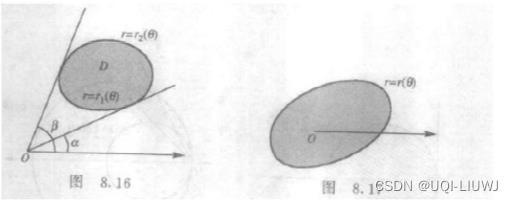
  • 对于左边的情况， 
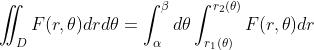
  • 对于右边的情况，

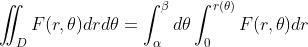
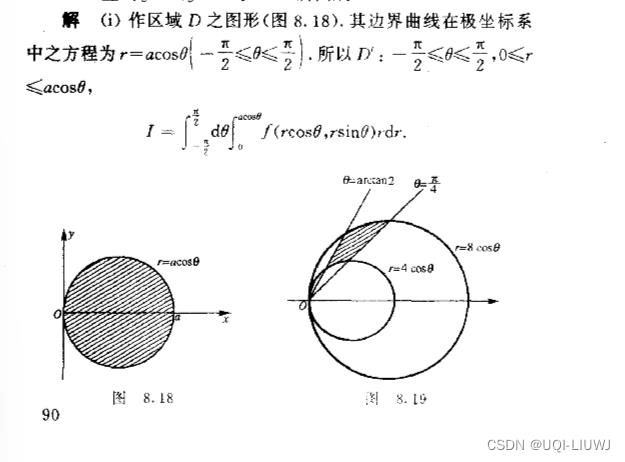
  3.1 举例

  

  

   

   

   4  二重积分的换元

  设函数f(x,y)在有界闭区域D上连续，如果变换 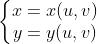满足以下三个条件

  • 将uv平面上区域D'一一对应到xy平面上的D
  • 变换函数x(u,v),y(u,v)在D'上连续，且有连续的一阶偏微商
  • 雅可比行列式 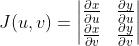在D'上不取零值

  则有换元公式

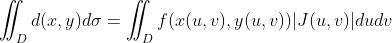
  注：可以证明上述三个条件可以适当地放宽：对于（1）和（3），可以允许个别点/个别曲线上不满足；对于（2），可以允许分段连续

  4.1 举例

  求二重积分 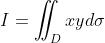 其中区域D是由抛物线 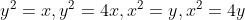围成的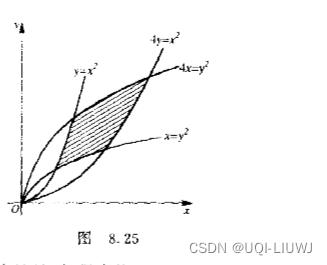

  

  这里无论有那种次序的累次积分，都需要将D分成几块，比较繁琐。

  不过如果我们把曲线边界表示为 

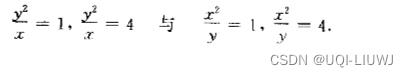
  时候，也就是进行变换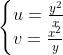时，可以迎刃而解。此时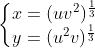

  雅可比矩阵

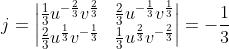
  所以原式

   

   

  开发者涨薪指南 48位大咖的思考法则、工作方式、逻辑体系

  以上是关于高等数学——二重积分的主要内容，如果未能解决你的问题，请参考以下文章

  吴裕雄--天生自然 高等数学学习：二重积分的计算方法

  Python人工智能之-三大数学难点 !

  高数基础知识整理11.二重积分

  人工智能数学基础 | 目录 | 00

  2017 4月14日

  数学知识整理：二重积分