第十一届蓝桥杯大赛决赛试题Java A组(试题解析)
Posted 潮浪之巅
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第十一届蓝桥杯大赛决赛试题Java A组(试题解析)相关的知识,希望对你有一定的参考价值。
本专栏将会从基础开始,循序渐进,每天刷一道算法题,也请大家多多支持。数据结构虽然难,但只要肯坚持,一定能学好,希望大家都能够从中有所收获。
专栏地址: 每日一道算法题专栏 数据结构专栏
本专栏的所有代码都将更新在Gitee上,项目地址:项目地址
相关数据结构演示软件:链接地址
数据结构在线演示地址:https://visualgo.net/zh https://algorithm-visualizer.org/
如果文章知识点有错误的地方,请指正!大家一起学习,一起进步。
如果感觉博主的文章还不错的话,还请关注、点赞、收藏三连支持一下博主哦
准备好了吗
Let’s go!
文章目录

试题 A: 合数个数
问题描述
一个数如果除了 1 和自己还有其他约数,则称为一个合数。
例如:1, 2, 3 不是合数,4, 6 是合数。请问从 1 到 2020 一共有多少个合数。
思路解析
在1-2020这些数中,构成有3部分:质数、合数、既非质数亦非合数,既非质数亦非合数只有数字"1"。
参考代码
// 1:不能有packet
// 2: 类名必须Main, 不可修改
import java.util.Scanner;
public class Main
//判断一个数是否为合数
public static boolean judge(int num)
for(int i = 2; i <= Math.sqrt(num); i++)
//有余数,则返回true
if(num%i == 0)
return true;
return false;
public static void main(String[] args)
int count = 0;
//1,2,3都不是合数,所以从4开始
for(int i = 4; i <= 2020; i++)
if(judge(i))
count++;
System.out.println(count);
试题 B: 含2天数
问题描述
小蓝特别喜欢 2,今年是公元 2020 年,他特别高兴,因为每天日历上都可以看到 2。
如果日历中只显示年月日,请问从公元 1900 年 1 月 1 日到公元 9999 年 12月 31 日,一共有多少天日历上包含 2。
即有多少天中年月日的数位中包含数字 2。
思路解析
- 区分闰年和平年
闰年的判断:
①整百年数除以400,无余为闰,有余为平
②非整百年数除以4,无余为闰,有余为平
- 依次按照判断哪些年份、月份、号数含有2
- 若年份中含有2,则直接加上该年总的天数(注意平年和闰年2月天数不同)
- 若年份中不含有2,实际只需判断2月和12月一共有多少天(注意平年和闰年2月天数不同),其中12月一共有31天。
- 若年份中不含有2,且月份中不含有2,即判断1、3、4、5、6、7、8、9、10、11这10个月中的号数一共有多少天含有2,这10个月的一共含有2的天数是固定的,即10*12天 = 120天。
参考代码
import java.util.Scanner;
public class Main
//判断年份y中是否含有2,如1902、2221都含有2
public static boolean isInclude2(int year)
while(year!=0)
if(year%10 == 2)
return true;
year /= 10;
return false;
//判断某年是否为闰年
public static boolean isLeap(int y)
//整百年数除以400,无余为闰,有余为平
if((y%100==0) && (y%400==0))
return true;
//非整百年数除以4,无余为闰,有余为平
if((y%100!=0) && (y%4==0))
return true;
return false;
public static void main(String[] args)
int startYear = 1900; //起始年份
int endYear = 9999; //结束年份
int numOneYear = 0; //记录某年中含有2的天数
int totals = 0; //记录总的含有2的天数
int numTenMonths = 120; //1、3、4、5、6、7、8、9、10、11这10个月含有2的天数
int num12Month = 31; //12月含有的天数
for(int y=startYear; y<=endYear; y++)
//判断该年份是否含有2
if(isInclude2(y))
//判断是闰年还是平年
if(isLeap(y)) numOneYear = 366;
else numOneYear = 365;
else
if(isLeap(y))
//是闰年则2月份为29天
numOneYear = num12Month + numTenMonths + 29;
else
//是平年则2月份为28天
numOneYear = num12Month + numTenMonths + 28;
totals += numOneYear;
System.out.println(totals);
试题C:本质上升序列
问题描述
小蓝特别喜欢单调递增的事物。
在一个字符串中,如果取出若干个字符,将这些字符按照在字符串中的顺序排列后是单调递增的,则成为这个字符串中的一个单调递增子序列。
例如,在字符串 lanqiao 中,如果取出字符 n 和 q,则 nq 组成一个单调递增子序列。类似的单调递增子序列还有 lnq、i、ano 等等。
小蓝发现,有些子序列虽然位置不同,但是字符序列是一样的,例如取第二个字符和最后一个字符可以取到 ao,取最后两个字符也可以取到 ao。小蓝认为他们并没有本质不同。
对于一个字符串,小蓝想知道,本质不同的递增子序列有多少个?
例如,对于字符串 lanqiao,本质不同的递增子序列有 21 个。它们分别
是 l、a、n、q、i、o、ln、an、lq、aq、nq、ai、lo、ao、no、io、lnq、
anq、lno、ano、aio。
请问对于以下字符串tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
本质不同的递增子序列有多少个?
思路解析
设str为题目中的目标字符串,定义dp[i]为以str[i]为结尾时的递增子序列的个数。因为
j<i,所以遍历j=0~i-1,有如下讨论:
- str[j] < str[i],此时dp[i]=dp[i]+dp[j]
- str[j] == str[i],此时dp[i]=dp[i]-dp[j]
- str[j] > str[i],此时是降序,不考虑
为了观察方便,就以数字2、1、3、8、5、7、4、5为例:
str dp[i] dp的值 递增子序列 2 dp[0] 1 2 1 dp[1] 1 1 3 dp[2] 3 3, 23, 13 8 dp[3] 6 8, 28, 18, 38, 238, 138 5dp[4] 6 5, 25, 15, 35, 235, 1357 dp[5] 12 7, 27, 17, 37, 237, 137, 57, 257, 157, 357, 2357, 1357 4 dp[6] 6 4, 24, 14, 34, 234, 134 5dp[7] 6 5, 25, 15, 35, 235, 135,45, 245, 145, 345, 2345, 1345由上面的表格可知,当str[j]=str[i]时,会出现重复的子序列,此时就要减去这一部分,也就是
1. str[j] < str[i],此时dp[i]=dp[i]+dp[j]的讨论。
参考代码
import java.util.Scanner;
public class Main
public static void main(String[] args)
String str = "tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl";
int result = 0;
int[] dp = new int[str.length()];
for(int i=0; i<str.length(); i++)
dp[i]=1;
for(int i=0; i<str.length(); i++)
for(int j=0; j<i; j++)
if(str.charAt(j) < str.charAt(i))
dp[i] += dp[j];
else if(str.charAt(j) == str.charAt(i))
dp[i] -= dp[j];
for(int i=0; i<str.length(); i++)
result += dp[i];
System.out.println(result);
试题D:咫尺天涯
问题描述
思路解析
首先,如果通过暴力打表,然后将所有相邻点差值的和累加起来,当然是不现实的。想想空间复杂度和时间复杂度就明白了。这里我们能够很容易得到空间复杂度是 O ( ( 3 n ) 2 ) O((3^n)^2) O((3n)2) ,估算一下当 n = 14 n=14 n=14时,内存至少需要 170445GB,所以用暴力的方式是不现实的。
这里我们将每一个n阶的图都看成一阶的,也就是说把每个n阶的图看成9个n-1阶的图,就转化成了一阶跟二阶的关系,根据二阶的和一阶的x,y之间的关系来逐层降阶。
虽然 n=14我们做不到,但是 n 比较小的时候还是能够处理的嘛。比如:n=1, n=2这样的。先写一个模拟出来,再找找规律看看。
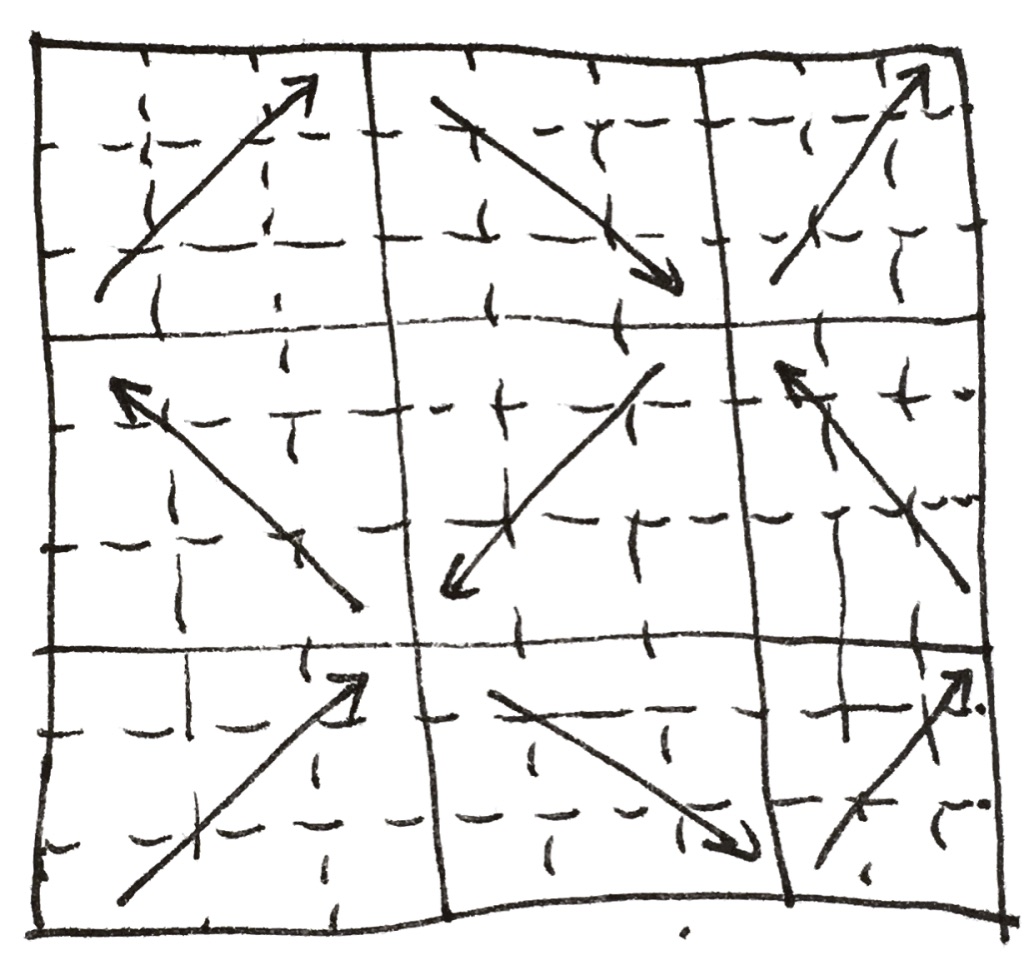
请先看下面两张图,分别为 1 阶皮亚诺曲线和 2 阶皮亚诺曲线大致走向示意图。
我们发现在所有的皮亚诺曲线中,大致走向只有四个方向:↗️、↖️、↘️、↙️,依次编号为1,2,3,4.
- ↗️
- ↖️
- ↘️
- ↙️
而皮亚诺曲线升阶(比如1阶变到2阶)过程,就是对基阶皮亚诺曲线进行扩展操作。比如我们看 11 阶升阶为 22 阶就是对↗️走向扩展为 9 个走向↗️↖️↗️ ↘️↙️↘️ ↗️↖️↗️. 到这里如果都能看明白,其他对这个题目解题就很有帮助了。我们接下来要做的就是将四个方向扩展出来的方向列表搞出来,这个可以从二阶扩展到三阶的皮亚诺曲线中得到。
- ↗️ 扩展为 ↗️↖️↗️ ↘️↙️↘️ ↗️↖️↗️ 对应编号为
121 343 121- ↖️ 扩展为 ↖️↗️↖️ ↙️↘️↙️ ↖️↗️↖️ 对应编号为
212 434 212- ↘️ 扩展为 ↘️↙️↘️ ↗️↖️↗️ ↘️↙️↘️ 对应编号为
343 121 343- ↙️ 扩展为 ↙️↘️↙️ ↖️↗️↖️ ↙️↘️↙️ 对应编号为
434 212 434到这里接下来就变得简单了,当然还有一点需要处理,那就是各个大致行走方向怎么接上的问题,比如:先↗️走,接下来需要↖️走,但是我应该怎样让↗️结束后的那个位置接上↖️开始的位置呢?
那么我们对于所有可能的组合进行的表示(当然并不是所有的方向组合都在这个方向中的,比如↗️接下来就不可能是↙️):
那对于大致方向与大致方向之间的连接关系我们也得到了。
下来就是把大致方向(↗️、↖️、↘️、↙️)表示成详细的行走方向(⬆️、⬇️、⬅️、➡️)即可。
皮亚诺曲线实现
Dir.java 详细行走方向类,后面需要用到。
public class Dir
public int ic;
public int jc;
public Dir(int _ic_, int _jc_)
this.ic = _ic_;
this.jc = _jc_;
DirUtil.java 方向处理工具类,核心部分,用于升阶扩展操作,以及将大致行走方向表示成详细的行走方向。
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class DirUtil
private static final Dir UP = new Dir(1, 0);
private static final Dir DOWN = new Dir(-1, 0);
private static final Dir RIGHT = new Dir(0, 1);
private static final Dir LEFT = new Dir(0, -1);
public static Dir[] dir1 = new Dir[]
UP, UP, RIGHT, DOWN, DOWN, RIGHT, UP, UP
;
public static Dir[] dir2 = new Dir[]
UP, UP, LEFT, DOWN, DOWN, LEFT, UP, UP
;
public static Dir[] dir3 = new Dir[]
DOWN, DOWN, RIGHT, UP, UP, RIGHT, DOWN, DOWN
;
public static Dir[] dir4 = new Dir[]
DOWN, DOWN, LEFT, UP, UP, LEFT, DOWN, DOWN
;
public static Dir[] getDir(DirTester.Point s, DirTester.Point t)
if (s.x < t.x && s.y < t.y) return dir1;
if (s.x < t.x && s.y > t.y) return dir2;
if (s.x > t.x && s.y < t.y) return dir3;
return dir4;
public static Dir[] getDirById(int __id__)
switch (__id__)
case 1:
return dir1;
case 2:
return dir2;
case 3:
return dir3;
case 4:
return dir4;
return null;
// 升阶扩展操作
public static List<Integer> expandDirGroup(List<Integer> list)
List<Integer> expandedList = new ArrayList<>();
for (int item : list)
switch (item)
case 1:
expandedList.addAll(Arrays.asList(1, 2, 1, 3, 4, 3, 1, 2, 1));
break;
case 2:
expandedList.addAll(Arrays.asList(2, 1, 2, 4, 3, 4, 2, 1, 2));
break;
case 3:
expandedList.addAll(Arrays.asList(3, 4, 3, 1, 2, 1, 3, 4, 3));
break;
case 4:
expandedList.addAll(Arrays.asList(4, 3, 4, 2, 1, 2, 4, 3, 4));
break;
return expandedList;
// 将大致行走方向展开为完整的行走方向
public static List<Dir> expandAsStepList(List<Integer> dirGroupList)
List<Dir> dirs = new ArrayList<>();
int prevDirId = 0;
for (int dirGroupId : dirGroupList)
Dir[] dirsTmp = getDirById(dirGroupId);
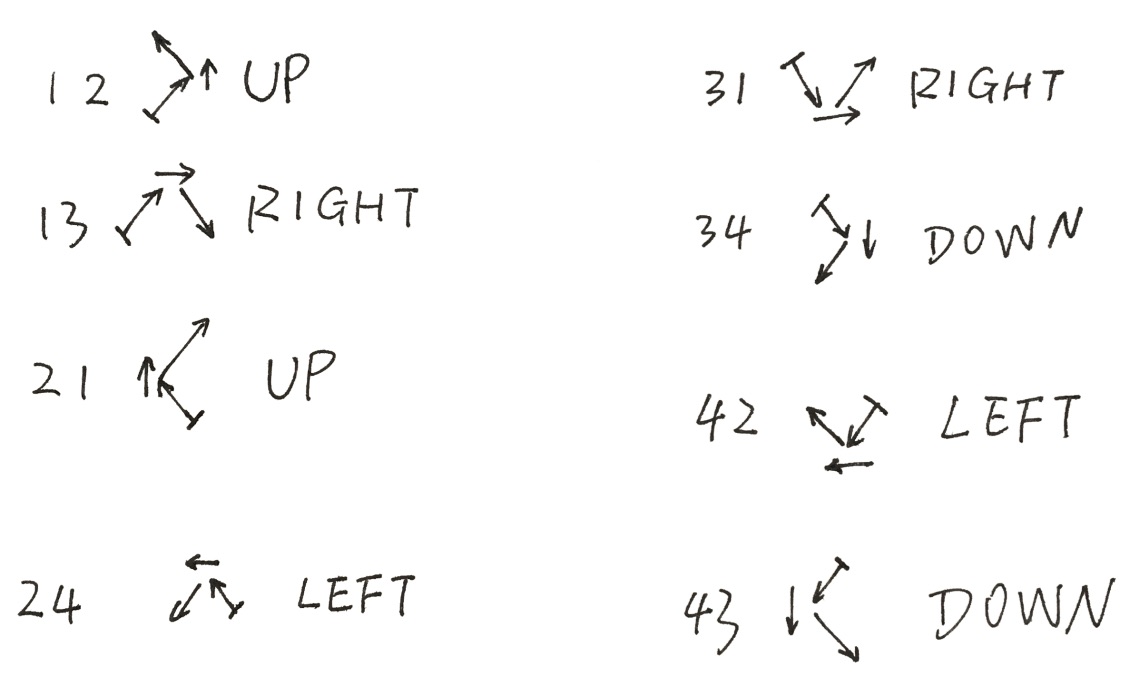
switch (prevDirId * 10 + dirGroupId)
case 12:
case 21:
dirs.add(UP);
break;
case 13:
case 31:
dirs.add(RIGHT);
break;
case 24:
case 42:
dirs.add(LEFT);
break;
case 34:
case 43:
dirs.add(DOWN);
break;
assert dirsTmp != null;
dirs.addAll(Arrays.asList(dirsTmp));
prevDirId = dirGroupId;
return dirs;
HilbertCurveTester.java 则是对曲线结果进行测试了。
import java.util.*;
public class HilbertCurveTester
static class Point
public int x, y;
public Point()
public Point(int x, int y)
this.x = x;
this.y = y;
public static int[][] genMap(int level)
if (level < 1)
return null;
int mapSize = pow(3, level);
int[][] a = new int[mapSize][mapSize];
List<Integer> dirGroupList = new ArrayList2022年6月第十三届蓝桥杯大赛软件赛全国决赛C++A组题解
目录
-
成绩与复盘
估分:0 + 0 + 10 + 10 + 2 + 15 + 10 + 8 + 10 + 0 = 65
成绩:全国二等奖中上
笔者估自己的分一直很准,至于这次比赛:
- 估分不会偏高,因为编程题基本上经过赛场上的对拍
- 估分不会偏低,不会装弱
经历与经验
笔者是一名退役的ACM同学,总共参加了三场蓝桥杯国赛,成绩依次是十一届CB国二、十二届CA国三、十三届CA国二。由于欠缺一点实力和运气,在ACM赛事上没取得什么成绩,但是自认为有些比赛经历和经验。蓝桥杯有很多地方确实做的不好,该骂还得骂,然后不可否认的是,它给很多比上不足(ACM区域赛)、或者压根没有参加算法竞赛(ACM省赛)的同学提供了一个更大众、更适合的比赛平台。对于蓝桥杯,要想取得满意的成绩,我认为最重要的是细心。虽然这个词看似是一个在哪都通吃的话术,但是对于蓝桥杯尤为重要:
-
认真对待。这是笔者吃过很多亏才明白的道理,当你想做好一件事的时候,或者说,当这件事做不好你会留有遗憾的时候,那就应该用谦卑的态度去做好这件事。比如蓝桥杯,我记得C/C++组必须要return 0,这在参赛手册上写得很清楚,但仍然每年都有很多同学犯这种低级错误。还有今年是在新的平台比赛,编程题提交框中,Ctrl+A不是快捷键,有不少同学修改代码没有覆盖之前提交的代码(这更多是平台的问题),这种问题其实也可以通过花一两分钟简单地检查一遍避免。
-
相比于其他比赛,细心在蓝桥杯上也体现得更为重要。比如ACM比赛、力扣周赛,错误提交会有罚时,在参加ACM比赛的时候,笔者和队友也都保持谨慎的态度,有时候写完了代码必须反复测试才敢提交,生怕返回错误。但是ACM比赛错误了还能继续提交,只是花费时间更多而已(当然,并不是说时间不重要,很多时候解题数一样,需要依靠花费时间更少来获奖),而蓝桥杯,一旦犯了低级错误(笔者在这次省赛中,青蛙那题因为写错一句代码,导致整题都挂了),导致的结果很可能是整道题差不多直接挂了。一种推荐的解决办法:程序对拍,不了解对拍的同学可以参考以上文章或者自行上网搜索,不再赘述。也正是省赛的低级错误,让我坚定了国赛一定要写对拍的决心,因此国赛虽然写出来的题目也不多,但是基本上都能保证正确。
-
比赛策略。一、题目难度不保证梯度上升。也就是说后面的题可能比前面的简单,那遇到卡题的情况,果然地选择跳过,换其他题目可能是制胜的关键。二、有部分得分。比如这次国赛的H题替换字符,暴力解法就有8分,这不比前面的RMQ、最短路什么的简单多了?一道题的数据范围直接决定了解题方法和题目难度。所以在最后一小时,一定要保证把所有题的小数据分拿到,它们真的很简单。
真诚地希望能够帮助到后来人
——2022.07.08
试题 A: 小蓝与钥匙

C(28,14)*错排
错排可以容斥或者递推
1286583532342313400
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 16;
long long dp[N];
int main()
long long ans = 1;
int ct = 2;
for (int i = 15; i <= 28; i++)
ans = ans * i;
while (ans % ct == 0 && ct <= 14)
ans /= ct, ct++;
dp[2] = 1, dp[3] = 2;
for (int i = 3; i <= 14; i++)
dp[i] = 1ll * (i - 1) * (dp[i - 1] + dp[i - 2]);
cout << ans * dp[14] << endl;
return 0;
试题 B: 排列距离

康托展开,注意是循环排列。
试题 C: 内存空间


预计得分:100%
模拟即可
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
const long long mod = 1e9 + 7;
string str;
void solve()
int n;
scanf("%d", &n);
getchar();
long long ans = 0;
for (int i = 1; i <= n; i++)
getline(cin, str);
string TP = "";
int m = str.size();
bool f = 0;
for (int i = 0; i < m; i++)
if (!f)
TP += str[i];
if (TP == "int" || TP == "long" || TP == "String")
f = 1;
continue;
if (TP == "String")
bool flag = 0;
for (int j = i; j < m; j++)
if (!flag)
if (str[j] == '\\"')
flag = 1;
continue;
if (str[j] == '\\"')
flag = 0;
continue;
ans++;
break;
if (str[i] == '[')
bool flag = 0;
long long res;
for (int j = i + 2; j < m; j++)
if (!flag)
if (str[j] == '[')
flag = 1, res = 0;
continue;
if (str[j] == ']')
flag = 0;
ans += res * (TP == "int" ? 4 : 8);
continue;
res = res * 10 + str[j] - '0';
break;
for (int j = i; j < m; j++)
if (str[j] == ',' || str[j] == ';')
ans += (TP == "int" ? 4 : 8);
break;
long long B = ans % 1024;
long long KB = ans / 1024 % 1024;
long long MB = ans / 1024 / 1024 % 1024;
long long GB = ans / 1024 / 1024 / 1024 % 1024;
if (GB)
printf("%lldGB", GB);
if (MB)
printf("%lldMB", MB);
if (KB)
printf("%lldKB", KB);
if (B)
printf("%lldB\\n", B);
int main()
solve();
return 0;
/*
1
long[] nums=new long[131072];
4
int a=0,b=0;
long x=0,y=0;
String s1=?? hello??,s2=??world??;
long[] arr1=new long[100000],arr2=new long[100000];
*/
试题 D: 最大公约数

预计得分:100%
如果数组中已经有
1
1
1,那么直接用
1
1
1平铺即可。
否则找出最小区间满足区间
G
C
D
=
1
GCD=1
GCD=1,用这个
1
1
1进行平铺。
寻找方法可以使用二分+RMQ。
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
const long long mod = 1e9 + 7;
const long long INF = 0x3f3f3f3f;
int a[N];
struct node
int l, r, g;
tr[N << 2];
void pushup(int k)
tr[k].g = __gcd(tr[k * 2].g, tr[k * 2 + 1].g);
void build(int k, int l, int r)
tr[k].l = l, tr[k].r = r;
if (l == r)
tr[k].g = a[l];
return;
int mid = l + r >> 1;
build(k * 2, l, mid);
build(k * 2 + 1, mid + 1, r);
pushup(k);
int query(int k, int L, int R)
if (tr[k].l == L && tr[k].r == R)
return tr[k].g;
int mid = (tr[k].l + tr[k].r) >> 1;
if (R <= mid)
return query(k * 2, L, R);
else if (L > mid)
return query(k * 2 + 1, L, R);
else
return __gcd(query(k * 2, L, mid), query(k * 2 + 1, mid + 1, R));
void solve()
int n;
scanf("%d", &n);
int ct = 0;
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
ct += a[i] == 1;
if (ct) //有1直接平铺
printf("%d\\n", n - ct);
return;
build(1, 1, n);
if (query(1, 1, n) != 1) //肯定不行
puts("-1");
return;
int min_step = INF;
for (int i = 1; i <= n; i++)
int l = i + 1, r = n, res = INF;
while (l <= r)
int mid = l + r >> 1;
if (query(1, i, mid) == 1)
res = mid - i;
r = mid - 1;
else
l = mid + 1;
min_step = min(min_step, res);
printf("%d\\n", min_step + n - 1);
int main()
solve();
return 0;
/*
3
4 6 9
5
6 4 6 10 5
*/
试题 E: owo

预计得分:10%
应该是个DP,刚开始没什么思路,后面也没时间想了,交了暴力。
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
int ans = 0;
string s[N];
int ct = 0;
int func()
int r = 0;
for (int i = 1; i <= 1e3; i++)
random_shuffle(s + 1, s + 1 + ct);
string tmp;
for (int i = 1; i <= ct; i++)
tmp += s[i];
int n = tmp.size();
int res = 0;
for (int i = 2; i < n; i++)
res += tmp[i - 2] == 'o' && tmp[i - 1] == 'w' && tmp[i] == 'o';
r = max(r, res);
return r;
void solve()
srand(time(NULL));
int n;
cin >> n;
for (int i = 1; i <= n; i++)
string str;
cin >> str;
if (str[0] != 'o' && str[0] != 'w' && str[(int)str.size() - 1] != 'o' && str[(int)str.size() - 1] != 'w') //剪枝
printf("%d\\n", ans);
continue;
else
s[++ct] = str;
ans = func();
printf("%d\\n", ans);
int main()
solve();
return 0;
试题 F: 环境治理


预计得分:100%
比较简单的一个题,二分+FLOYD求最短路。时间复杂度
n
3
l
o
g
m
n^3logm
n3logm,其中m为把所有路径清理到下限的所需天数(开个
1
e
8
、
1
e
9
1e8、1e9
1e8、1e9都行)。
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N = 105;
const long long mod = 1e9+7;
const int INF= 0x3f3f3f3f;
int w[N][N];
int ww[N][N];
int minn[N][N];
int n , q;
int check(int day)
int ans =0 ;
for(int i =0; i<n; i++)
for(int j =0; j<n; j++)
ww[i][j]=w[i][j];
for(int i =0; i<n; i++)
int val = day/n+(day%n>=i+1?1:0);
for(int j =0 ; j<n; j++)
ww[i][j]-=val,ww[j][i]-=val;
for(