雅礼集训1.2 T3取石子

Posted 2023-04-01 tanjunming2020

题目大意

有$n$堆石子，第$i$堆有$x_i$个。$Alice$和$Bob$轮流取石子，先后手未定，$Alice$每次从一堆中取走$a$个，$Bob$每次从一堆中取走$b$个，不能操作者输。

不难发现只有四种情况：$Alice$必胜，$Bob$必胜，先手必胜，后手必胜。你需要选若干堆石子（总共有$2^n$种选法），$Alice$和$Bob$只能在你选出的堆中取，问以上四种情况对应的方案数。

$1\le n\le 10^5$，$1\le a,b,x_i\le 10^9$

题解

不妨设$a<b$

首先，我们可以将每一堆的石子数量模$(a+b)$。为什么可以这样呢？

如果模$(a+b)$后可以证明一方必胜

• 如果这一方是后手，则只要先手拿的那一堆大于等于$(a+b)$，则取那一堆；否则按最优策略取对应的那一堆
• 如果这一方是先手，则先按最优策略取一堆，然后它就是后手了，接着按后手的方法来取就行了

然后我们可以分类讨论，不妨设$a<b$。

• 如果$x_i<a$，则这一类没有用
• 如果$a\le x_i<b$，则存在则$a$必胜
• 如果$b\le x_i<2a$，答案只与这一类的奇偶性相关
• 如果$x_i\ge 2a$，在没有第二类石子的条件下
  • 存在至少两个则$a$必胜
  • 存在一个且第三类石子个数为偶数则先手必胜
  • 存在一个且第三类石子个数为奇数则$a$必胜
  • 不存在且第三类石子个数为奇数则先手必胜
  • 不存在且第三类石子个数为偶数则后手必胜

时间复杂度为$O(n)$。

code

#include<bits/stdc++.h>
using namespace std;
const int N=100000;
int n,a,b,fl=0,x[100005];
int v1=0,v2=0,v3=0,v4=0;
long long ans1=0,ans2=0,ans3=0,ans4=0,jc[N+5],ny[N+5];
long long mod=1000000007;
long long mi(long long t,long long v)
	if(!v) return 1;
	long long re=mi(t,v/2);
	re=re*re%mod;
	if(v&1) re=re*t%mod;
	return re;

void init()
	jc[0]=1;
	for(int i=1;i<=N;i++) jc[i]=jc[i-1]*i%mod;
	ny[N]=mi(jc[N],mod-2);
	for(int i=N-1;i>=0;i--) ny[i]=ny[i+1]*(i+1)%mod;

long long C(int x,int y)
	return jc[x]*ny[y]%mod*ny[x-y]%mod;

int main()

	init();
	scanf("%d%d%d",&n,&a,&b);
	if(a>b)
		fl=1;swap(a,b);
	
	for(int i=1;i<=n;i++)
		scanf("%d",&x[i]);
		x[i]=x[i]%(a+b);
		if(x[i]<a) ++v1;
		else if(x[i]>=a&&x[i]<b) ++v2;
		else if(x[i]>=b&&x[i]<2*a) ++v3;
		else ++v4;
	
	long long tmp=mi(2,v1+v3+v4);
	for(int i=1;i<=v2;i++)
		ans1=(ans1+C(v2,i)*tmp%mod)%mod; 
	
	tmp=mi(2,v1);
	for(int i=0;i<=v3;i++)
		if(i&1) ans3=(ans3+C(v3,i)*tmp%mod)%mod;
		else ans4=(ans4+C(v3,i)*tmp%mod)%mod;
	
	tmp=mi(2,v1)*v4%mod;
	for(int i=0;i<=v3;i++)
		if(i&1) ans1=(ans1+C(v3,i)*tmp%mod)%mod;
		else ans3=(ans3+C(v3,i)*tmp%mod)%mod;
	
	tmp=mi(2,v1+v3);
	for(int i=2;i<=v4;i++)
		ans1=(ans1+C(v4,i)*tmp%mod)%mod;
	
	if(fl) swap(ans1,ans2);
	printf("%lld %lld %lld %lld",ans1,ans2,ans3,ans4);
	return 0;

「6月雅礼集训 2017 Day8」gcd

【题目大意】

定义times(a, b)表示用辗转相除计算a和b的最大公约数所需步骤。

那么有：

1. times(a, b) = times(b, a)

2. times(a, 0) = 0

3. times(a, b) = times(b, a mod b) + 1

对于$1 \leq x \leq A, 1 \leq y \leq B$，求times(A, B)的最大值，以及有多少对数取到了最大值。

多组数据。

$T \leq 3 \times 10^5, 1 \leq A,B \leq 10^{18}$

【题解】

我们打一个1000以内，times(x, y) = 13的表

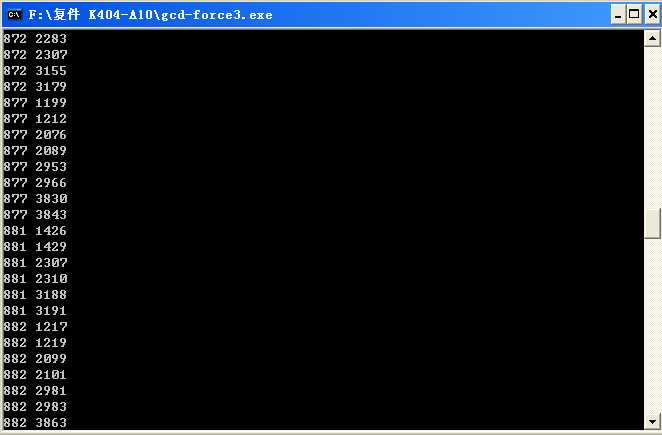
我们定义好数对为：$(x,y)$满足不存在$1 \leq x‘ \leq x, 1\leq y‘\leq y$，使得times(x‘, y‘) > times(x, y)

那么明显答案肯定是好数，我们发现，答案中的很多数都是由$(x,y)$经过$(x, x+ky)$变换来的。

那么答案很多，但是$(x,y)$这样的数少，我们定义这样的数为极好数。

严格定义为$x \leq fib_{x+2}, y \leq fib_{x+2}$且times(x, y) = k的好数。

我们可以发现并证明（显然），好数只要1步就能变成极好数。

那么我们只要求出极好数，就能推出好数的数量了。

容易发现极好数很少，只要暴力求即可。

比如当times = 13的时候，极好数的个数只有13.。。

（就是把上面所有好数简化过后）

那么我们就能暴力求啦

发现times = x的极好数，是根据times = x-1的极好数(x, y)经过变换(y, x+ky)而来。那么我们只要根据极好数的定义求即可。

复杂度$O(Qlog^2(A))$

# include <vector>
# include <stdio.h>
# include <string.h>
# include <iostream>
# include <algorithm>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;

const int N = 1e5 + 10, M = 2e5 + 10, F = 105;
const int mod = 1e9 + 7;

inline ll getll() {
    ll x = 0; char ch = getchar();
    while(!isdigit(ch)) ch = getchar();
    while(isdigit(ch)) x = x * 10 + ch - ‘0‘, ch = getchar();
    return x;
}

ll fib[F];

struct pa {
    ll a, b;
    pa() {}
    pa(ll a, ll b) : a(a), b(b) {}
    friend bool operator == (pa a, pa b) {
        return a.a == b.a && a.b == b.b;
    }
    friend bool operator < (pa a, pa b) {
        return a.a < b.a || (a.a == b.a && a.b < b.b);
    }
    friend bool operator > (pa a, pa b) {
        return a.a > b.a || (a.a == b.a && a.b > b.b);
    }
};

vector<pa> g[M];

int times = 0;
inline int gcd(ll a, ll b) {
    if(a < b) swap(a, b);
    if(b == 0) return a;
    ++times;
    return gcd(b, a%b);
}

inline int calc(ll a, ll b) {
    times = 0;
    gcd(a, b);
    return times;
}

inline void gg(int x) {
    pa t; g[x].clear();
    for (int i=0; i<g[x-1].size(); ++i) {
        t = g[x-1][i];
        ll y = t.b; swap(t.a, t.b);
        for (t.b += y; t.b <= fib[x+2]; t.b += y) 
            if(calc(t.a, t.b) == x) g[x].push_back(t);
    }
    sort(g[x].begin(), g[x].end());
    g[x].erase(unique(g[x].begin(), g[x].end()), g[x].end());
}

ll A, B, ans, tem;
inline void sol() {
    A = getll(), B = getll(); 
    if(A > B) swap(A, B);
    ans = 1; tem = 0;
    for (int i=2; i<90; ++i)
        if(fib[i] <= A && fib[i+1] <= B) ans = i;
        else break;    
    printf("%d ", ans);
    if(ans == 1) {
        printf("%d\n", A % mod * (B % mod) % mod);
        return ;
    } else {
        for (int i=0; i<g[ans-1].size(); ++i) {
            ll a = g[ans-1][i].a, b = g[ans-1][i].b;
            if(b <= A) tem += (B-a)/b, tem %= mod;
            if(b <= B) tem += (A-a)/b, tem %= mod;
        }
    }
    printf("%lld\n", tem);
}

int main() {
//    freopen("gcd.in", "r", stdin);
//    freopen("gcd.out", "w", stdout);
    fib[0] = 1, fib[1] = 1;
    for (int i=2; i<=90; ++i) fib[i] = fib[i-1] + fib[i-2];
    g[1].push_back(pa(1ll, 2ll)), g[1].push_back(pa(1ll, 3ll));
    for (int i=2; i<=88; ++i) gg(i);
    int T; cin >> T;
    while(T--) sol();
    return 0;
}

View Code

upd: 加了个读入优化跑了rk2