数据结构:栈和队列(详细讲解)
Posted 小鱼不会骑车
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构:栈和队列(详细讲解)相关的知识,希望对你有一定的参考价值。
🎇🎇🎇作者:
@小鱼不会骑车
🎆🎆🎆专栏:
《数据结构》
🎓🎓🎓个人简介:
一名专科大一在读的小比特,努力学习编程是我唯一的出路😎😎😎
栈和队列
栈
一. 栈的基本概念
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
在我们的常见生活中,我们在使用浏览器啊,写代码啊,或者说制作视频都会发现有一个返回键,例如我们在用文件夹在访问内容时,不小心点错文件,进入了一个不是自己想要查找的文件时,我们便可以通过上方的返回键来返回上一个页面。
这里涉及到的就是栈,也是栈经常使用的场景,当然!不同的程序他们的底层会用不同的代码来实现,但是不变的就是栈这个思想,我们只需要了解栈的这个数据结构就行。
1. 栈的定义
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶
出栈:栈的删除操作叫做出栈,出数据在栈顶
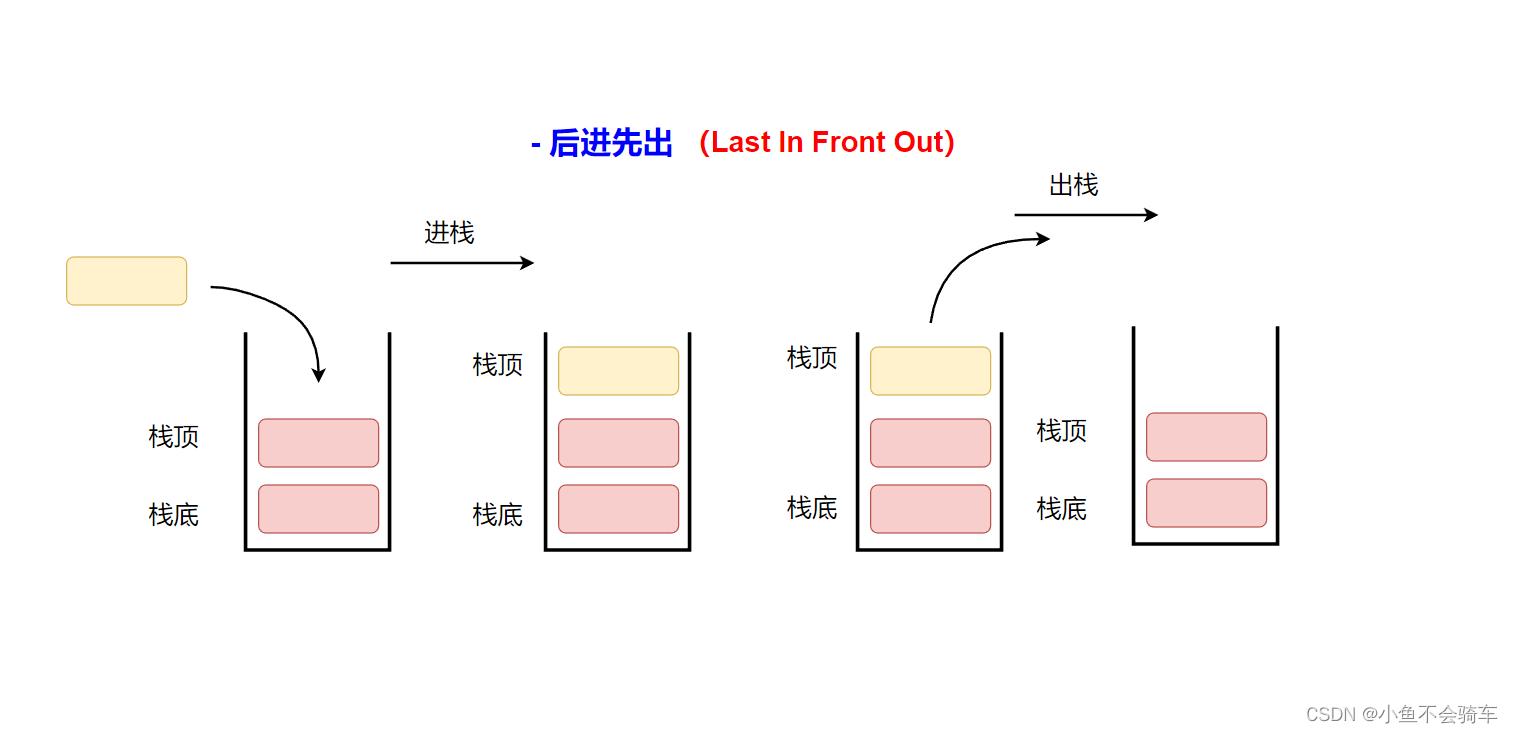
栈在现实生活中的例子:

2. 栈的常见基本操作
| 方法 | 功能 |
|---|---|
| Stack() | 构造一个空的栈 |
| E push(E e) | 将e入栈 |
| E pop() | 将栈顶元素出栈并返回 |
| E peek() | 获取栈顶元素 |
| int size() | 获取栈中有效元素个数 |
| boolean empty() | 检测栈是否为空 |
二. 栈的顺序存储结构
1. 栈的顺序存储
采用顺序存储的栈称为顺序栈,它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素,同时附设一个指针(top)指示当前栈顶元素的位置。
top的第一种初始化方法
对于top其实有两种初始化的方法,一种就是初始化为0,
public class MyStack
int []array;
int top;//记录栈顶位置
int capacity;//容量
public MyStack(int x)
this.top=0;//初始化为0
array=new int[x];//初始化一个x大小的数组
capacity=x;
public MyStack()
this.top=0;//初始化为0
array=new int[4];//默认初始化为4个大小的数组
capacity=4;
对于top 初始化为0,其实就是每次栈顶添加新元素时,都是先进行赋值,再top++,并且还需要对栈满进行判断(top初始化为0时添加元素和判断栈满的条件如下)
public void push(int x)
//判断栈满
if(top==capacity)
//扩容
array[top]=x;
top++;
如图:
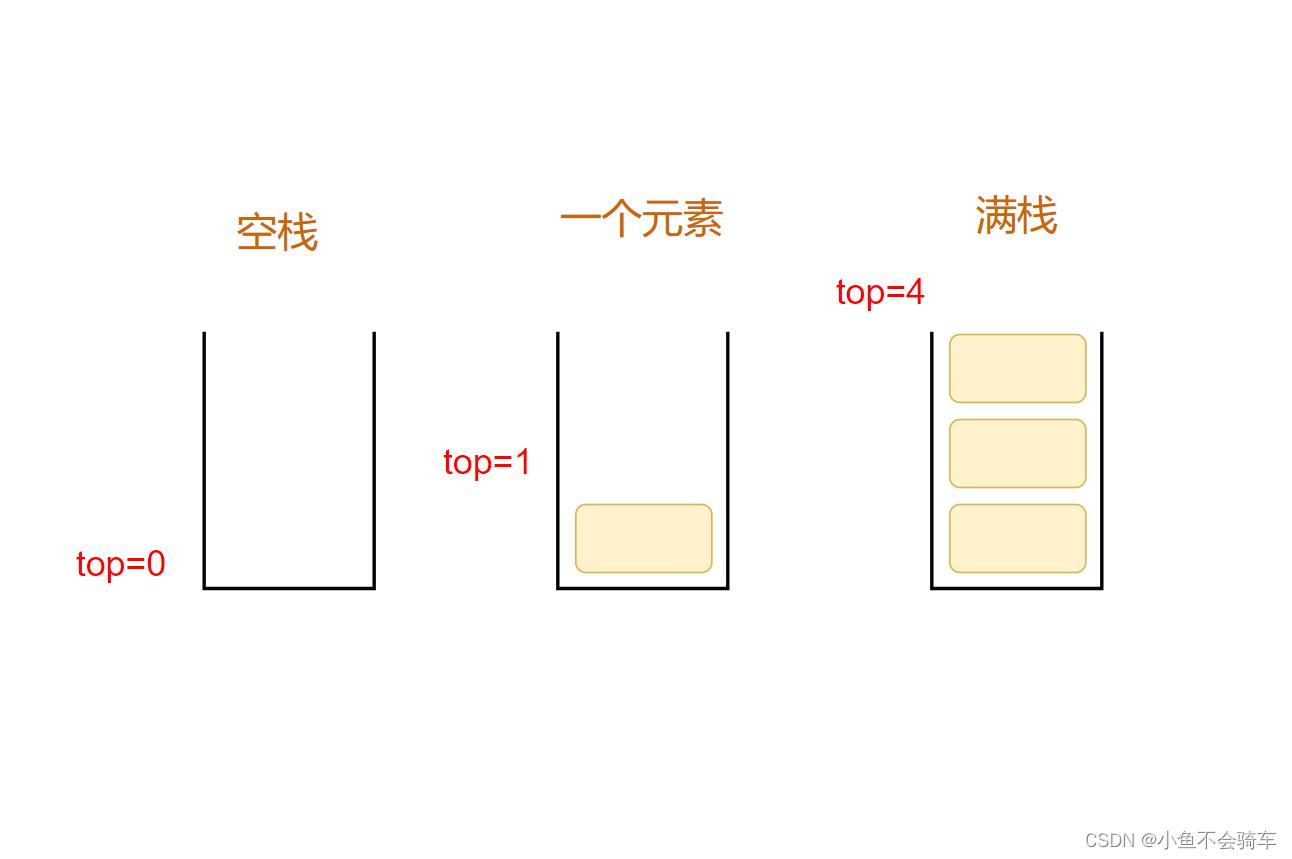
top的第二种初始化方法
当我的top初始化为-1时,由于我们添加元素需要从0下标开始添加,所以我们需要先top++,再赋值,此时我们的top记录的就是栈顶元素的下标,那么判满的话,就需要和capacity-1进行对比
public class MyStack
int []array;
int top;//记录栈顶位置
int capacity;//容量
public MyStack(int x)
this.top=-1;//初始化为-1
array=new int[x];//初始化一个x大小的数组
capacity=x;
public MyStack()
this.top=-1;//初始化为-1
array=new int[4];//默认初始化为4个大小的数组
capacity=4;
public void push(int x)
//判断栈满
if(top==capacity-1)
//扩容
top++;
array[top]=x;
如图:
此时的top就是栈顶元素对应的下标
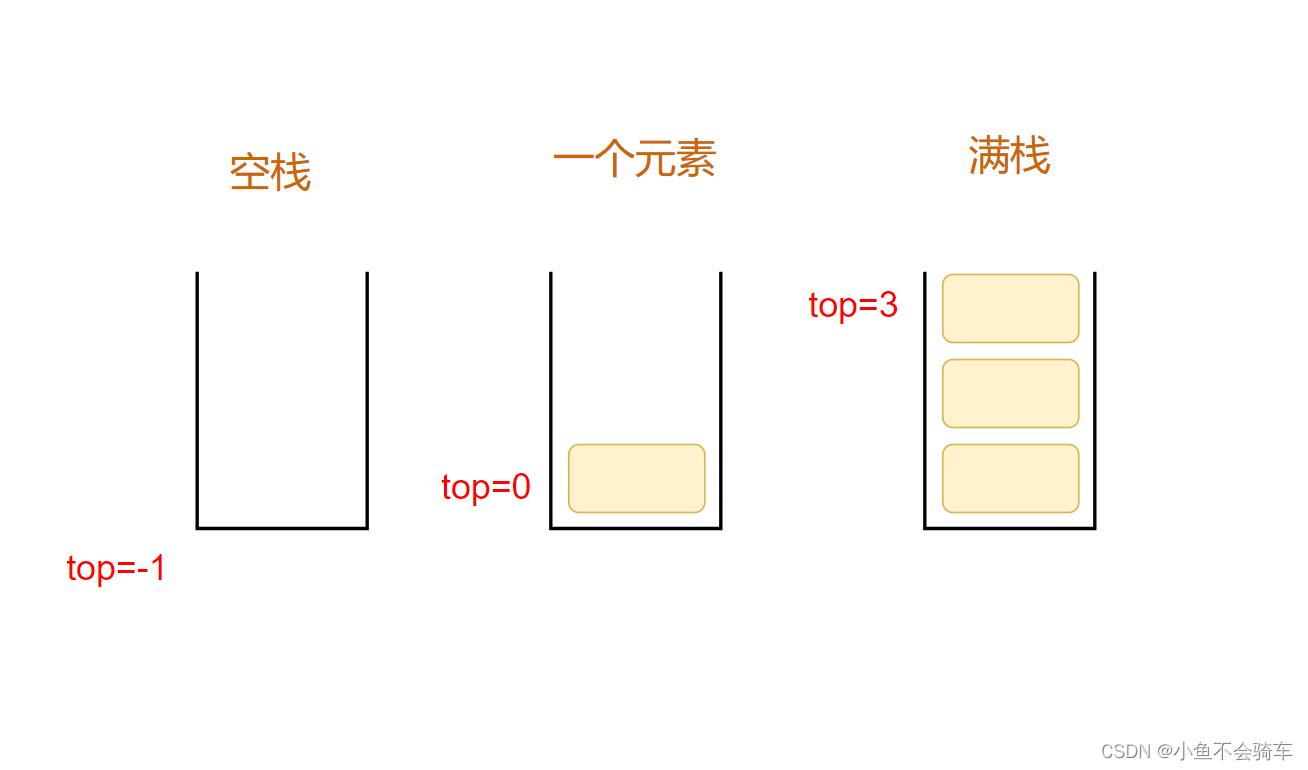
2. 栈的基本方法
(1) 初始化
//两个构造方法
public MyStack(int x)
this.top=-1;
array=new int[x];//初始化一个x大小的数组
capacity=x;
public MyStack()
this.top=-1;
array=new int[4];//默认初始化为4个大小的数组
capacity=4;
(2) 判空+判满(top初始化为-1)
//判空,当我的top为-1时就是没有元素
public boolean empty()
return top==-1;
//判满,当我的top+1==capacity时就代表栈满了
public boolean full()
return top+1==capacity;
(3) 进栈
public void push(int x)
//判断栈满
if(full())
//每次栈满扩容二倍
array=Arrays.copyOf(array,2*capacity);
capacity*=2;
top++;
array[top]=x;
(4) 出栈
//出栈
public int pop()
if(empty())
throw new ArrayEmptyException("栈空");
//先返回栈顶元素再--
return array[top--];
//自定义异常,当栈为空时抛出异常
class ArrayEmptyException extends RuntimeException
public ArrayEmptyException()
//构造方法
public ArrayEmptyException(String message)
super(message);
(5) 读取栈顶元素
public int peek()
if(empty())
throw new ArrayEmptyException("栈空");
//直接返回栈顶元素
return array[top];
3. 进栈出栈变化形式
我们现在已经简单了解了栈的特性,那么大家思考一下,这个最先进栈的元素只能是最后出栈嘛?
答案是不一定的!因为栈虽然限制了线性表的插入和删除的位置,但是并没有对元素的进出进行时间限制,也可以理解为,在不是所有元素都进栈的情况下,事先进去的元素也可以出栈,只要保证是栈顶元素出栈就可以。
举例来说,如果我们现在是有 3个整型数字元素1,2,3 依次进栈,会有哪些出栈次序呢?
- 第一种(最容易理解的):1,2,3依次进栈,再依次出栈,出栈次序是3,2,1.
- 第二种:1进栈,1出栈,2进栈,3进栈,3出栈,2出栈,出栈次序是1 ,3, 2.
- 第三种:1进栈,1出栈,2进栈,2出栈,3进栈,3出栈,出栈次序是1 ,2 ,3.
- 第四种:1进栈,2进栈,2出栈,1出栈,3进栈,3出栈,出栈次序是2, 1, 3.
- 第五种:1进栈,2进栈,2出栈,3进栈,3出栈,1出栈,出栈次序是2 ,3, 1.
- 那我们的出栈次序可以是3 1 2嘛?答案是不可以,因为3进栈后,此时栈内一定是有1,2,此时栈顶是2,并且1在2的下面,由于只能从栈顶弹出,又因为不可以直接跳过2去拿到1,所以此时不会出现 1 比 2 优先出栈的情况。
对于栈的变化,光三个元素就有五种出栈次序,那么五个元素,甚至更多的元素,那么它的出栈变化会更多,所以这个知识点我们一定要弄明白!
这里有道题,大家可以试着做一下:
- 若进栈序列为 1,2,3,4 ,进栈过程中可以出栈,则下列不可能的一个出栈序列是()
A: 1,4,3,2 B: 2,3,4,1 C: 3,1,4,2 D: 3,4,2,1
答案是:c
4. 共享栈(双栈)
其实对于共享栈,就是尽量减少内存的浪费,就像吃饭一样,煮方便面一袋不够吃,两袋吃不完,那你就可以找一个小伙伴一起吃,然后煮三袋,这样就不会吃不完了,并且还都能吃饱,这里开个玩笑,真正的用法在下面。
(1) 共享栈的概念
利用栈底位置相对不变的特征,可让两个顺序栈共享一个一维数组空间,将两个栈的栈底分别设置在共享空间的两端,两个栈顶向共享空间的中间延伸,如下图所示
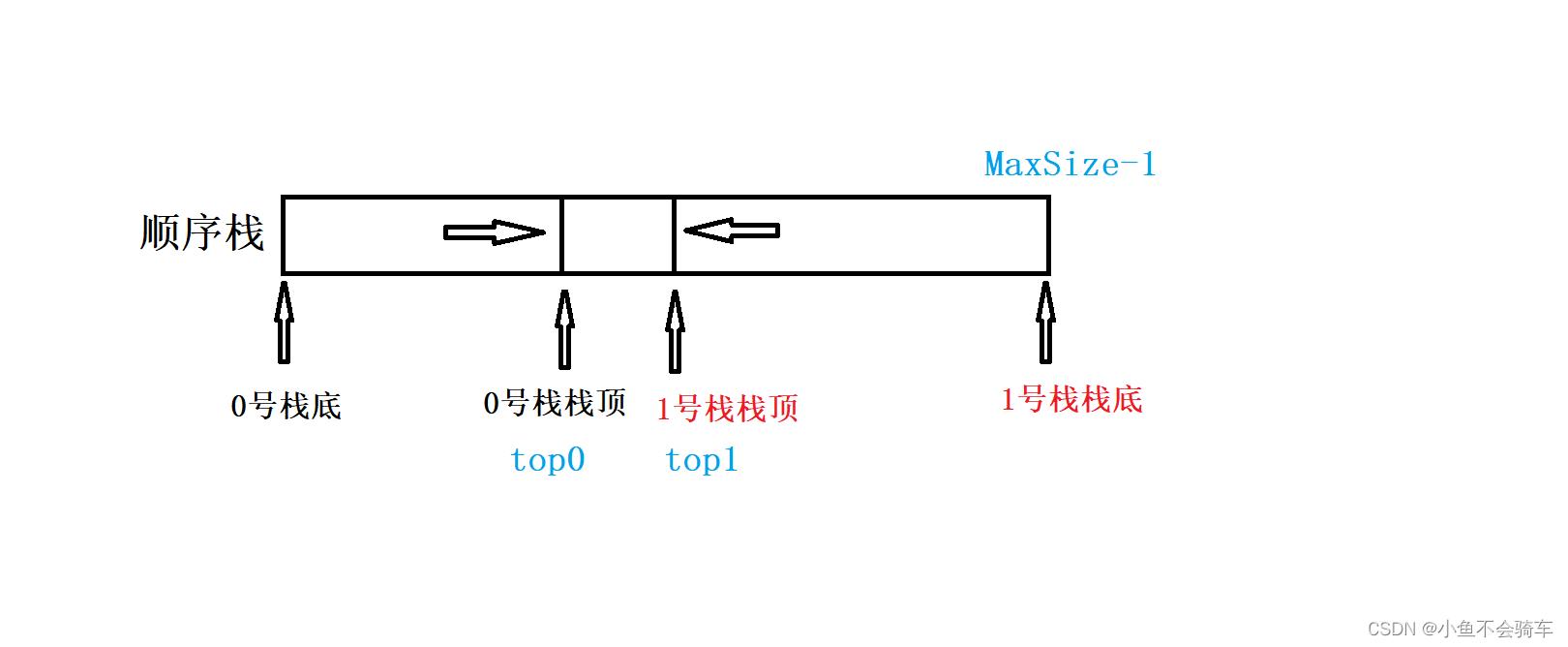
当我的top0==-1时,0号栈底为空,当我的top1==MaxSize时,1号栈底为空,当我的top0+1==top1时,判断为栈满,0号栈进栈时top0先加一再赋值,1号栈进栈时top1先减一再赋值,0号出栈时先保存当前元素再减一,1号栈出栈时和0号栈的出栈操作恰好相反。
(2) 共享栈的空间结构
代码如下:
public class SharedStack
int[]array;//定义一个数组成员
int top0;//记录0号栈的栈顶
int top1;//记录1号栈的栈顶
//构造方法,可以自己设置大小的数组
public SharedStack(int x)
array=new int[x];
top0=-1;
top1=x;
public SharedStack()
//由于共享栈不好扩容,所以直接开辟50个大小的数组
array=new int[50];
top0=-1;
top1=4;
(3) 共享栈进栈
由于是双端栈,所以我们需要对它调用不同的栈进行不同的写法,也就是需要判断是0号栈还是1号栈,分别写出对于的push.
public void push(int x,int stackNumber)
//判断栈是否满了
if(top0+1==top1)
exit(0);
//通过stackNumber来控制调用0号栈或1号栈
if(stackNumber==0)
top0++;
array[top0]=x;
else
top1--;
array[top1]=x;
(4) 共享栈出栈
public int pop(int stackNumber)
//判断调用几号栈
if(stackNumber==0)
//判空
if(top0==-1)
System.out.println("栈空");
exit(0);
else
return array[top0--];
else if(stackNumber==1)
//判空
if(top1==array.length)
System.out.println("栈空");
exit(0);
else
return array[top1++];
System.out.println("stackNumber输入错误");
//输入的stackNumber错误所以返回-1
//我们认为-1就是输入错误
return -1;
共享栈常用场景
一般的常用场景是,两个栈的空间需求有相反关系时,也就是一个栈增长,一个栈缩小的情况,例如你去买菜,你买了一斤白菜,那么卖家就少了一斤白菜,就这样我进,你出,才会使两栈空间的存储方法有更大的意义,否则如果我一直买菜,但是卖家也在一直进菜,那么很快就会因为栈满而溢出了。
当然,这个只是针对两个数据类型相同的栈设计的一个技巧,如果是不相同的栈,那么这么做反而会使问题变得更加复杂,所以大家要注意!
三. 栈的链式存储结构
1. 链栈
我们不仅可以通过顺序表实现栈,也是可以通过链表来实现的,但是有个前提,因为我们的顺序表实现的栈,它的插入和删除时间复杂度是O(1),那么如果想通过链表来实现栈,那么我们就需要考虑时间复杂度能否达到O(1),我们如果是通过双向链表来实现栈的话,因为双向链表本身含有尾结点的指针,所以它的插入和删除的时间复杂度是O(1),那么我们可以通过单链表来实现嘛?
答案也是可以的 !
我们可以通过头插头删来实现栈,由于我们单链表的头插,头删的时间复杂度都是O(1),并且我们的头插头删也满足了栈的先进后出的特性. 在链栈没有结点时,我们规定此时的head指向null.
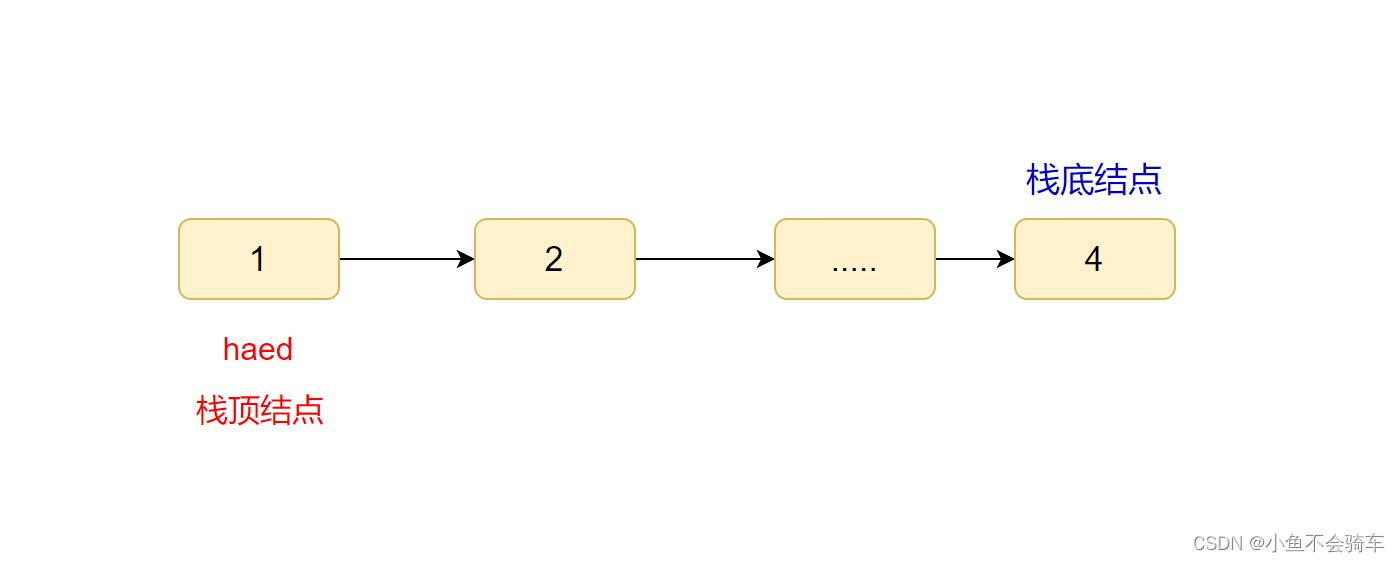
链栈的优点
由于我们是通过链表来实现的栈所以可以称为链栈,链栈几乎不会存在栈满的现象除非内存已经没有可以使用的空间了,如果真的发生,那么说明此时计算机已经内存被占满处于即将死机崩溃的情况,而不是这个链栈是否溢出的问题。
链栈的优点:
- 便于多个栈共享存储空间,提高内存利用率。
- 几乎不会存在栈满的情况
2. 链栈的基本方法
(1) 链栈的入栈
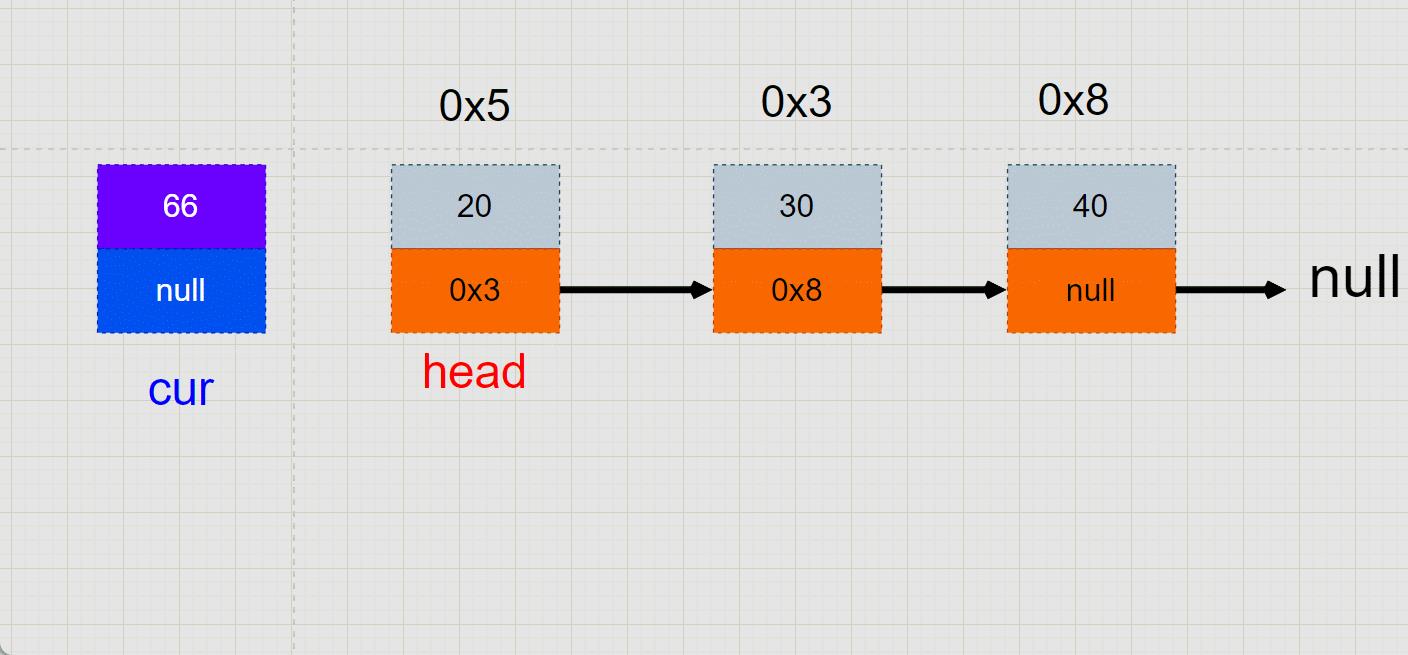
链栈的结构代码:
public class MyLinkedStack
static class Node
//单链表需要的next和val
public Node next;
public int val;
//构造方法
public Node(int val)
this.val = val;
//成员变量head
public Node head;
压栈/入栈:
public void push(int x)
//创建一个新节点
Node node=new Node(x);
//不管我的head是否为空,都可以将node的下一个结点指向head
node.next = head;
//head成为新结点
head=node;
(2) 链栈的出栈
用变量n保存要删除结点得值,头节点指向下一个结点,返回n.
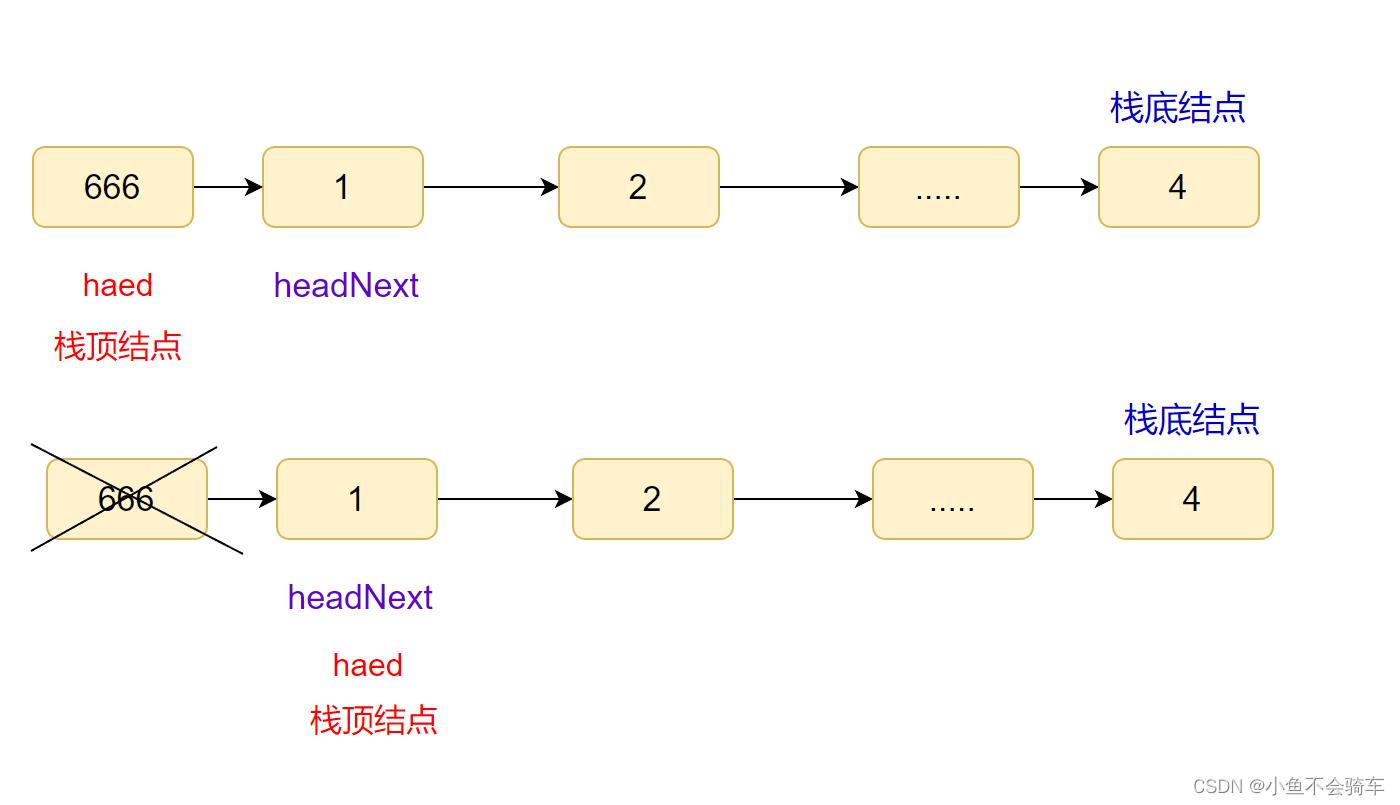
public int pop()
//判空,如果为空返回-1
if(empty())
return -1;
//记录头节点的值
int n=head.val;
//头指针指向下一个结点
head=head.next;
return n;
3. 对比链栈和顺序栈
链栈的进栈push和出栈pop操作都很简单,时间复杂度均为O(1)。
对比一下顺序栈与链栈,它们在时间复杂度上是一样的,均为O(1)。对于空间性能,顺序栈需要事先确定一个固定的长度,可能会存在内存空间浪费的问题,但它的优势是存取时定位很方便,而链栈则要求每个元素都有指针域,这同时也增加了一些内存开销,但对于栈的长度无限制。所以它们的区别和线性表中讨论的一样,如果栈的使用过程中元素变化不可预料,有时很小,有时非常大,那么最好是用链栈,反之,如果它的变化在可控范围内,建议使用顺序栈会更好一些。
6
6
四. 栈的应用——递归
1. 递归的定义

我们在写递归时需要注意的就是边界条件,一个递归必须要具有的就是边界条件,如果没有,那么递归将会一直进行下去,直到内存被栈满,最后程序崩溃。
我们用求数字的阶乘举例,例如我们想要求5的阶乘,那么我们可以写一个函数.
public static int func(int n)
//递归打印n的阶层
if(n==1)
return 1;
//每次返回当前的n*前一个值
return n*func(n-1);
public static void main(String[] args)
System.out.println(func(5));
如果用画图解释就是:
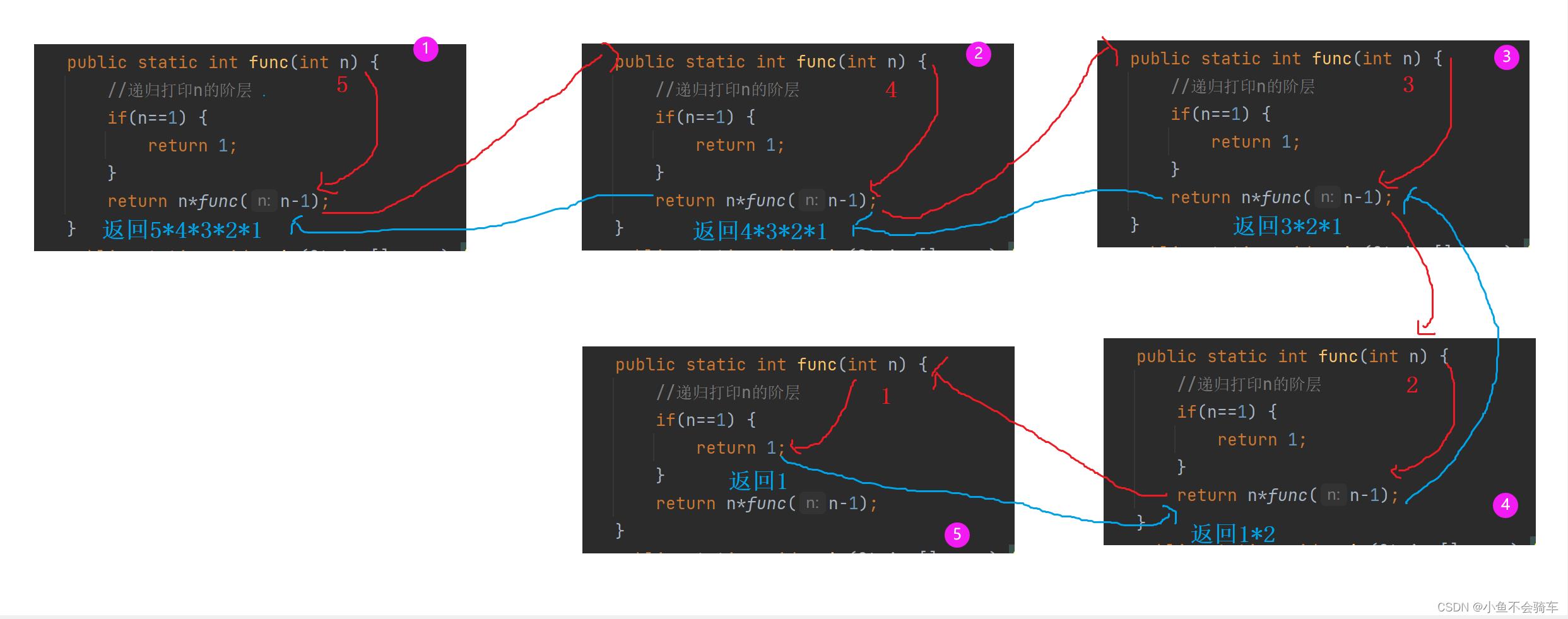
必须注意递归模型不是能是循环定义的,其必须满足下面的条件
- 递归表达式(递归体)
- 边界条件(递归出口)
递归的优点就是能够将原始问题转化为属性相同单规模较小的问题。
在递归调用的过程中,系统为每一层的返回点、局部变量、传入实参等开辟了递归工作栈来进行数据存储,递归次数过多容易造成栈溢出等。而其效率不高的原因是递归调用过程中包含很多重复的计算。
如下图:
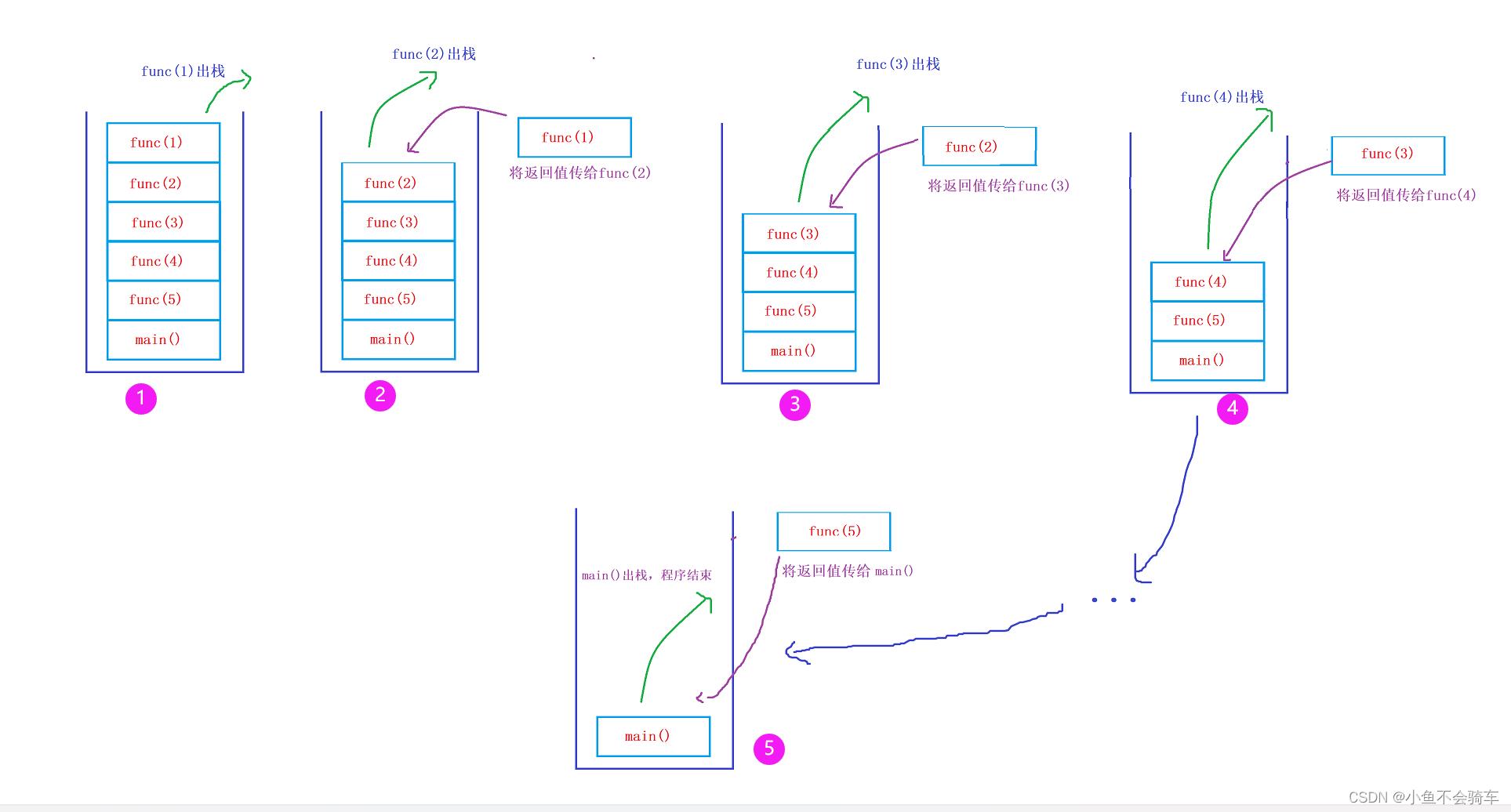
如图可知,程序每往下递归一次,就会把运算结果放到栈中保存,直到程序执行到临界条件,然后便会把保存在栈中的值按照先进后出的顺序一个个返回,最终得出结果。
五. 栈的应用——逆波兰表达式求值
逆波兰表达式求值也可以叫做后缀表达式求值,我们把平时所用的标准四则运算表达式,也就是例如 " ( A + B )* C / ( D - E ) "叫做中缀表达式,因为所有的运算符号都在俩数字之间。
表达式求值是程序设计语言编译中一个最基本的问题,它的实现是栈应用的一个典型范例,中缀表达式不仅依赖运算符的优先级,而且还要处理括号。
相反:对于后缀表达式,它的运算符在操作数的后面,在后缀表达式中已经考虑了运算符的优先级,没有括号,只有操作数和运算符。例如上述讲到的中缀表达式( A + B )* C / ( D - E ),它对应的后缀表达式就是A B + C * D E - /。
后缀表达式计算规则:从左到右遍历表达式的每个数字和符号,遇到是数字就进栈,遇到是符号,就将处于栈顶两个数字出栈,进项运算,运算结果进栈,一直到最终获得结果。
后缀表达式 A B + C * D E - /求值的过程需要 步,如下表所示:
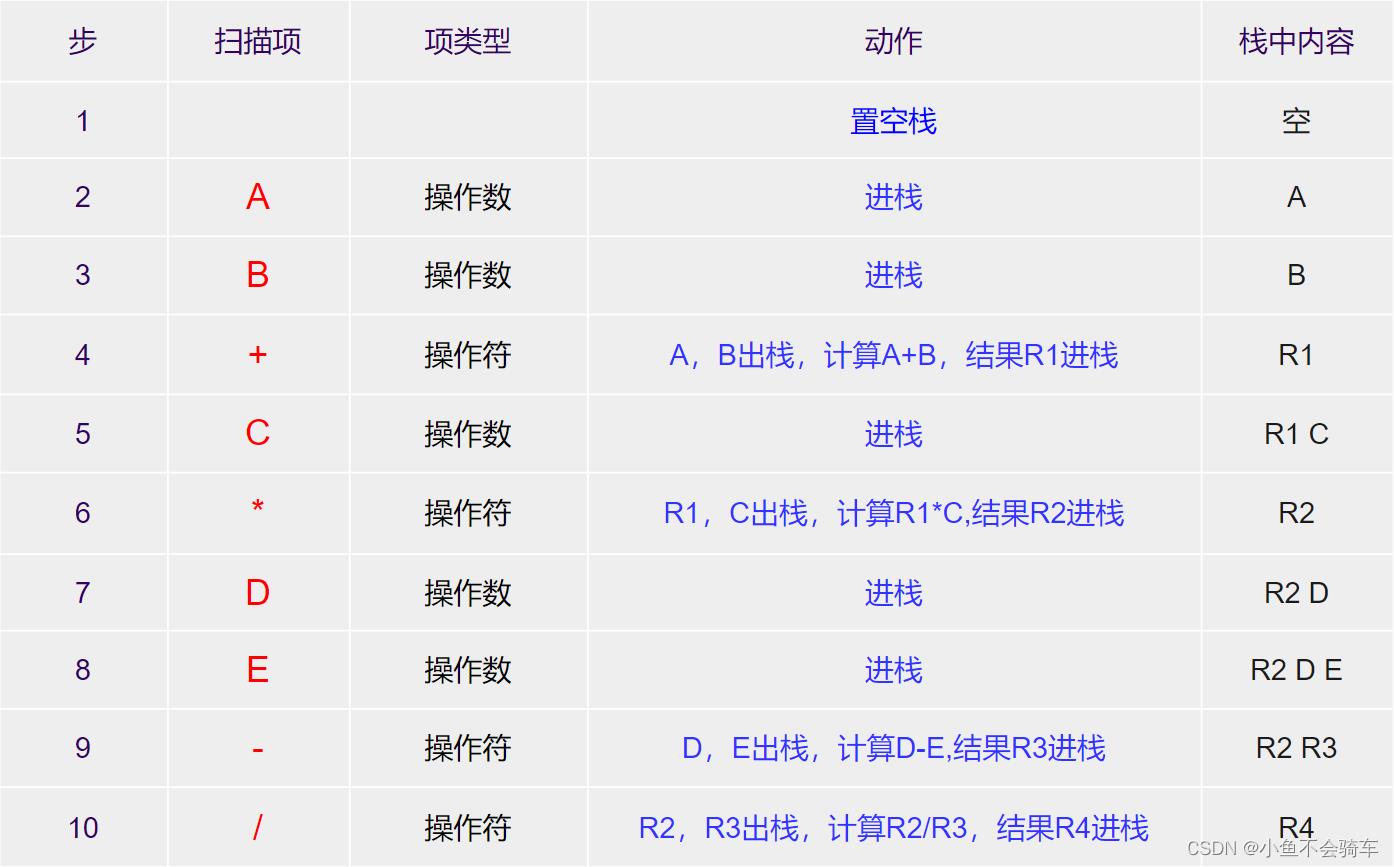
六. 栈的应用——中缀表达式转后缀表达式
前面已经对中缀表达式进行了大概了解,也就是所有的运算符号都在两数字的中间,现在我们的问题就是中缀到后缀的转化。
规则:从左到右遍历中缀表达式的每个数字和符号,若是数字就输出,即成为后缀表达式的一部分;若是符号,则判断其与栈顶符号的优先级,是右括号或优先级低于栈顶符号(乘除优先加减)则栈顶元素依次出栈并输出,并将当前符号进栈,一直到最终输出后缀表达式为止。
例:将中缀表达式a + b − a ∗ ( ( c + d ) / e − f ) + g 转化为相应的后缀表达式。
分析:需要根据操作符的优先级来进行栈的变化,我们用icp来表示当前扫描到的运算符ch的优先级,该运算符进栈后的优先级为isp,则运算符的优先级如下表所示[isp是栈内优先( in stack priority)数,icp是栈外优先( in coming priority)数]。

我们在表达式后面加上符号‘#’,表示表达式结束。具体转换过程如下:
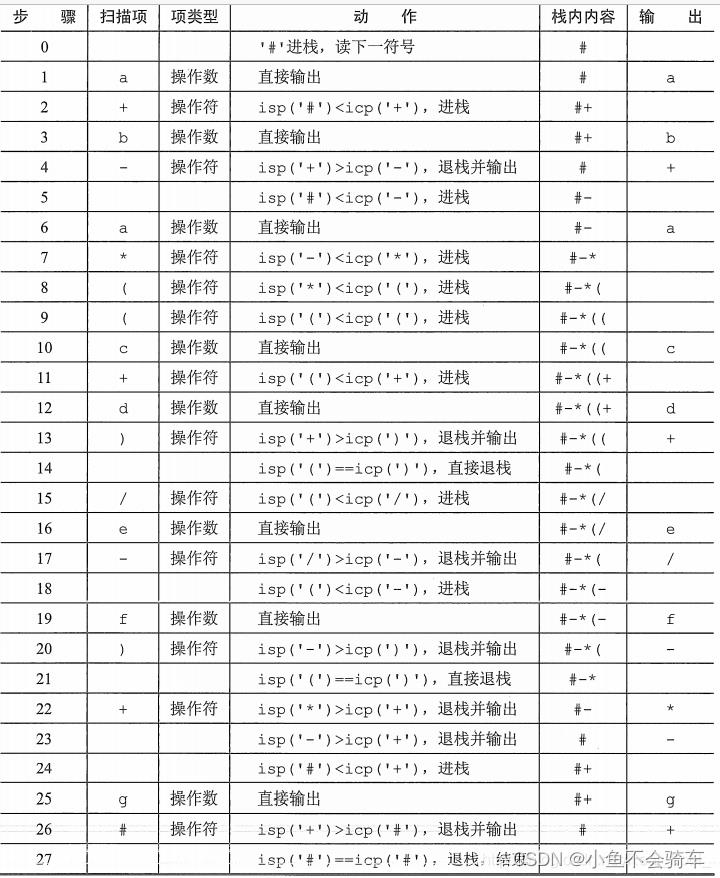
即相应的后缀表达式为a b + a c d + e / f − ∗ − g +。
从刚才的推导中你会发现,要想让计算机具有处理我们通常的标准(中缀)表达式的能力,最重要的就是两步:
- 将中缀表达式转化为后缀表达式(栈用来进出运算的符号)
- 将后缀表达式进行运算得到结果(栈用来进出运算的数字)
队列
一. 队列的基本概念
1. 队列的定义
队列(Queue) 只是允许在一端进行插入操作,而在另一端进行删除操作的线性表。
队列是一种先进先出(First In First Out)的线性表,简称FIFO。允许插入的一端称为队尾,允许删除的一端称为队头。
如图:
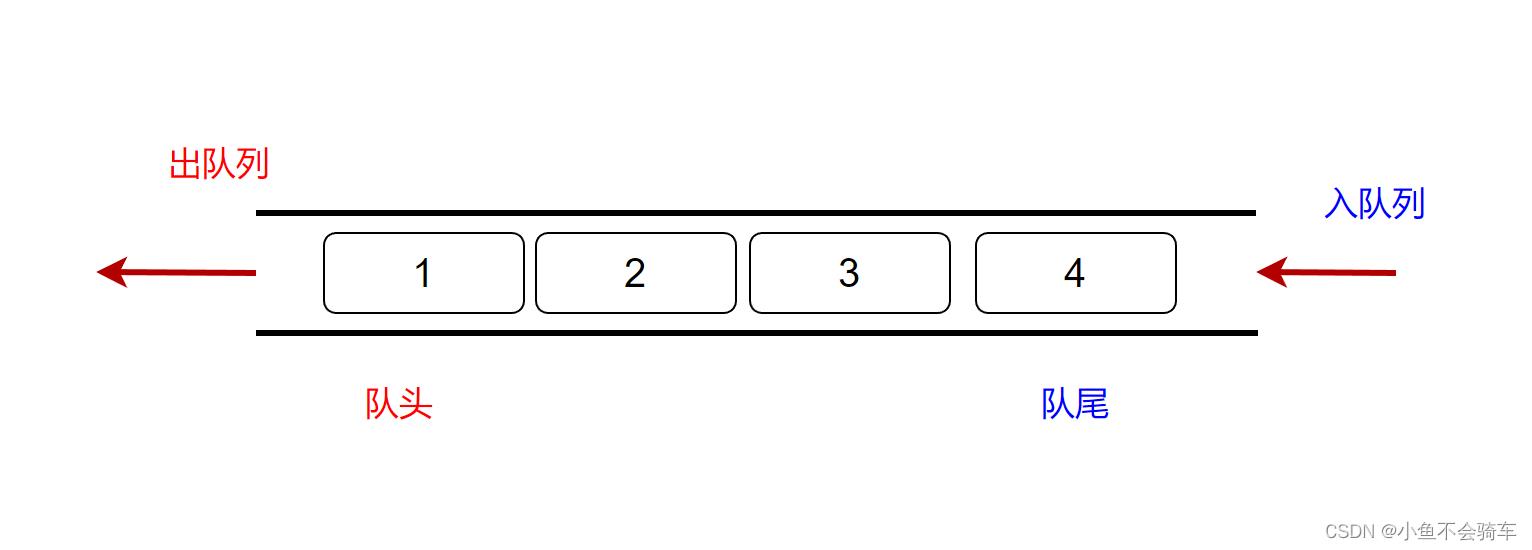
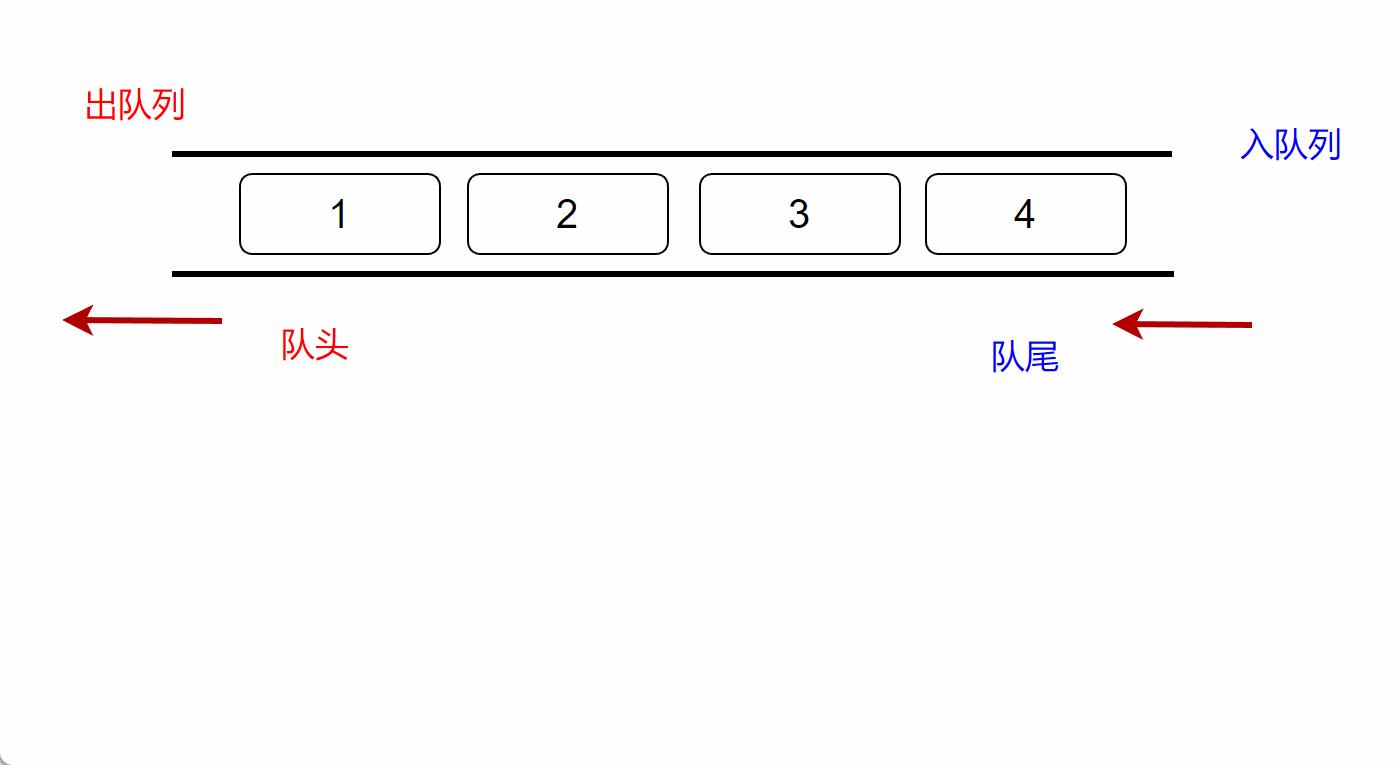
进出队列如图
进队列:

出队列:
我们一般在医院看见的出号机就是通过队列来实现的,按顺序取号,先取号的就会先被叫到,这有个好处就是,省去了复杂的排队,在你领完号之后就可以找个地方休息了,坐等叫号就行。
队头(Front):允许删除的一端,又称队首。
队尾(Rear):允许插入的一端。
空队列:不包含任何元素的空表。
2. 队列的常见基本操作
| 方法 | 功能 |
|---|---|
| boolean offer(E e) | 入队列 |
| E poll() | 出队列 |
| peek() 获取队头元素 | 获取队头元素 |
| int size() | 获取队列中有效元素个数 |
| boolean isEmpty() | 检测队列是否为空 |
二. 队列的顺序存储结构
1.顺序队列
队列的顺序实现是指分配一块连续的存储单元存放队列中的元素,并附设两个指针:队头指针 front 指向队头元素,队尾指针 rear 指向队尾元素的下一个位置。
队列的顺序存储类型可以描述为:
public class MyQueue
int []array;
int front;//记录队头
int rear;//记录队尾
public MyQueue(int n)
//控制一次开辟多少内存
array=new int[n];
public MyQueue()
//默认开辟四个内存
array=new int[4];
初始状态:(队列为空):front=rear=0。
进栈操作:队不满时,先给队尾下标对应的数组赋值,再队尾指针加1。
出栈操作:队不为空,先取出队头的元素,再队头指针减1。
进栈操作如图:

出栈操作:

假溢出:队列出现“上溢出”,然而却又不是真正的溢出,所以是一种“假溢出”。
大家看下图:在我的队尾指针=5时,说明队列已经满了,但是在下标为0和1的位置还是空闲的,我们称这种现象为“ 假溢出 ”(所以一般的队列会使用循环队列或者链表实现)
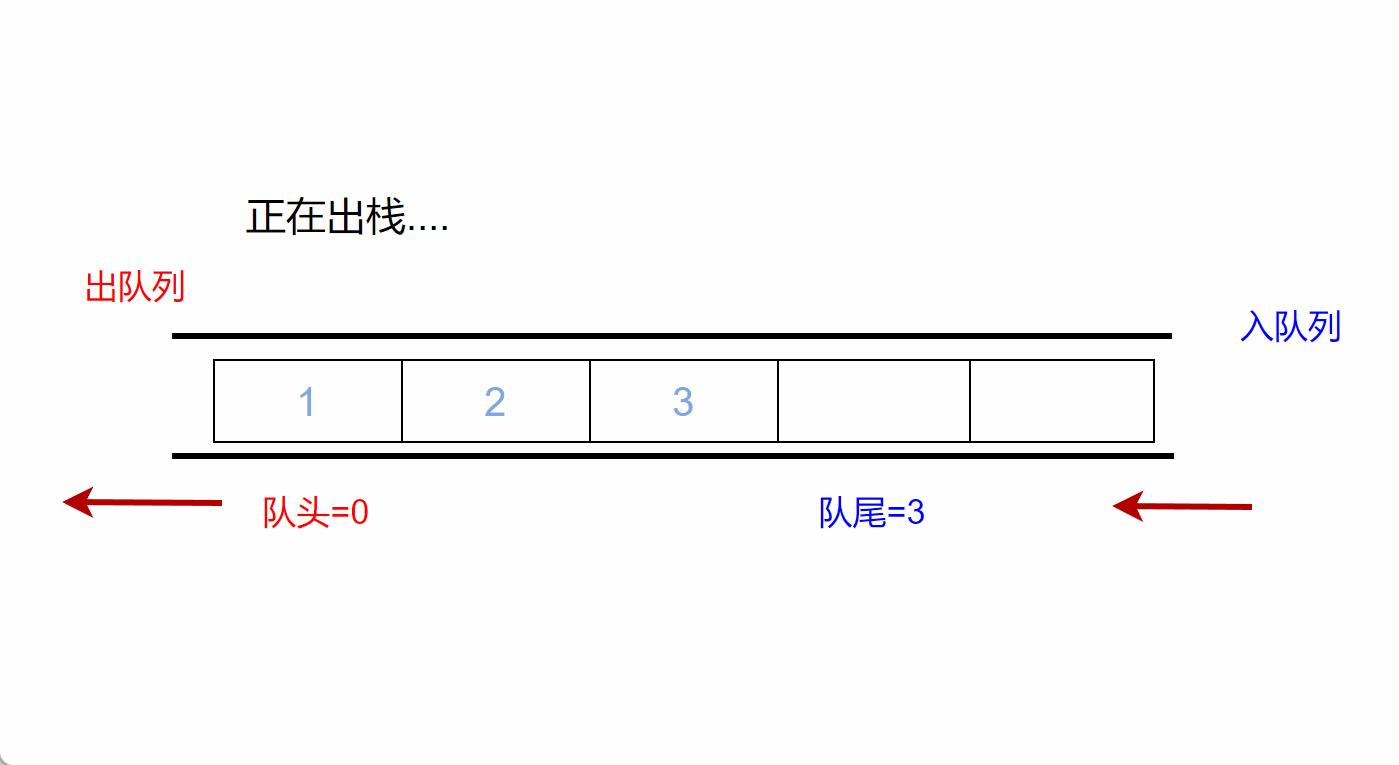
2.循环队列
解决假溢出的方法就是后面满了,就再从头开始,也就是头尾相接的循环。我们把队列的这种头尾相接的顺序存储结构称为循环队列。
当队首指针front = array.length-1后,再前进一个位置就自动到0,这可以利用除法取余运算(%)来实现。
下面是循环队列需要用到的一些公式,后续介绍。
初始时:front =rear=0。
判空:front=rear
判满:(rear+1)%array.length
队首指针进1:front = (front + 1) % array.length
队尾指针进1:rear = (rear + 1) % array.length
队列长度:(rear - front + array.length) % array.length
循环队列如图(下图中下标应该是从0开始,小鱼不小心写成了1,但是对于判断下面的推论没什么影响):
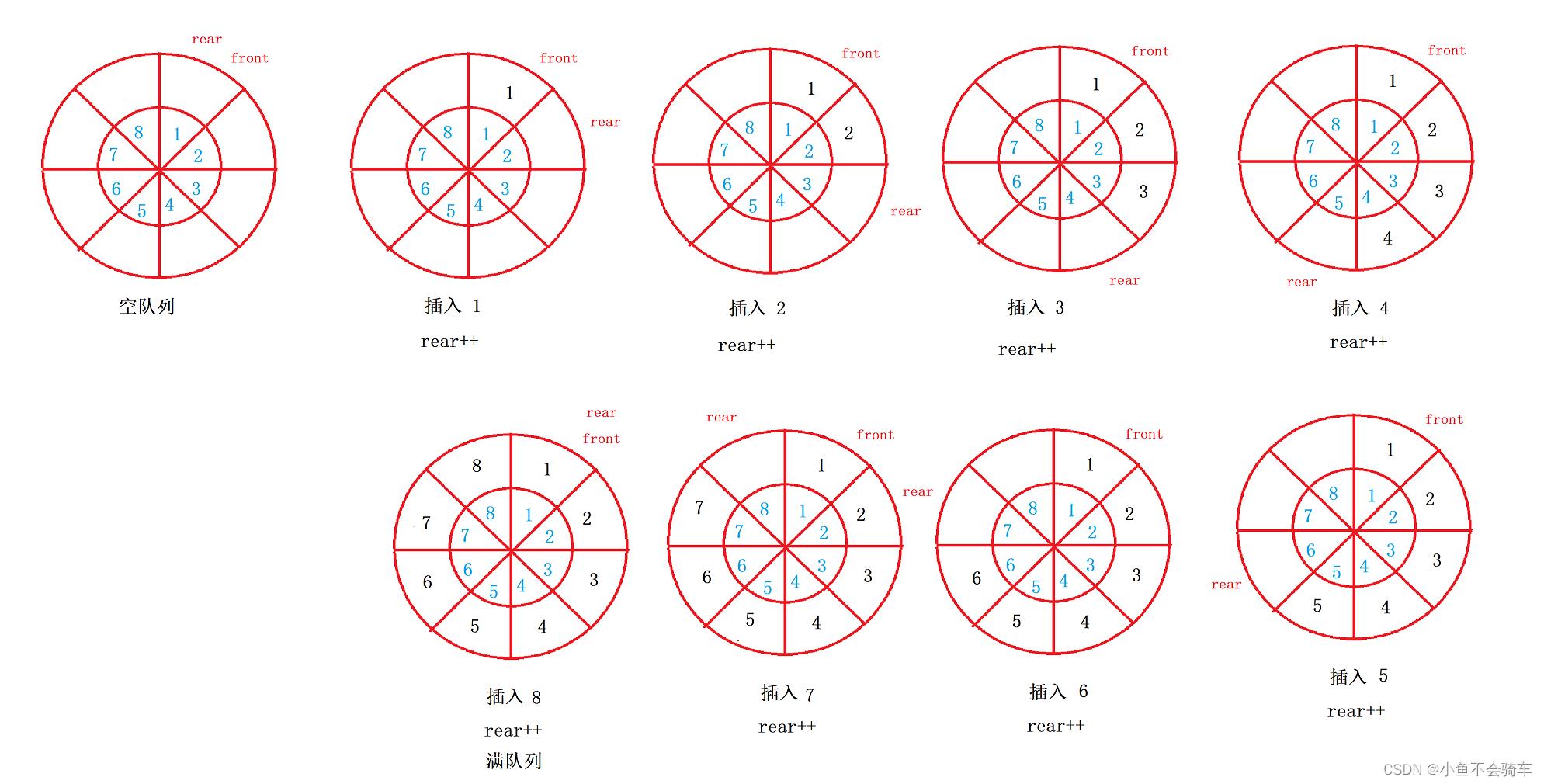
我们需要思考一个问题:如何判断这个循环队列是空队列,还是满队列?
我们可以看到,在 rear==front 时,即使空队列又是满队列,这就很麻烦,该如何解决呢?
-
方法(1):我们可以创建一个成员变量
size,只有当size==队列长度时,才判满,当size==0为空队列。 -
方法(2) :我们也可以牺牲一个空间:
-
方法(3):类型中增设tag 数据成员,以区分是队满还是队空。tag 等于0时,若因删除导致 front = = rear ,则为队空;tag 等于 1 时,若因插入导致 front == rear ,则为队满。
这里着重讲解第二种方法(在这里将下标更正为0)!
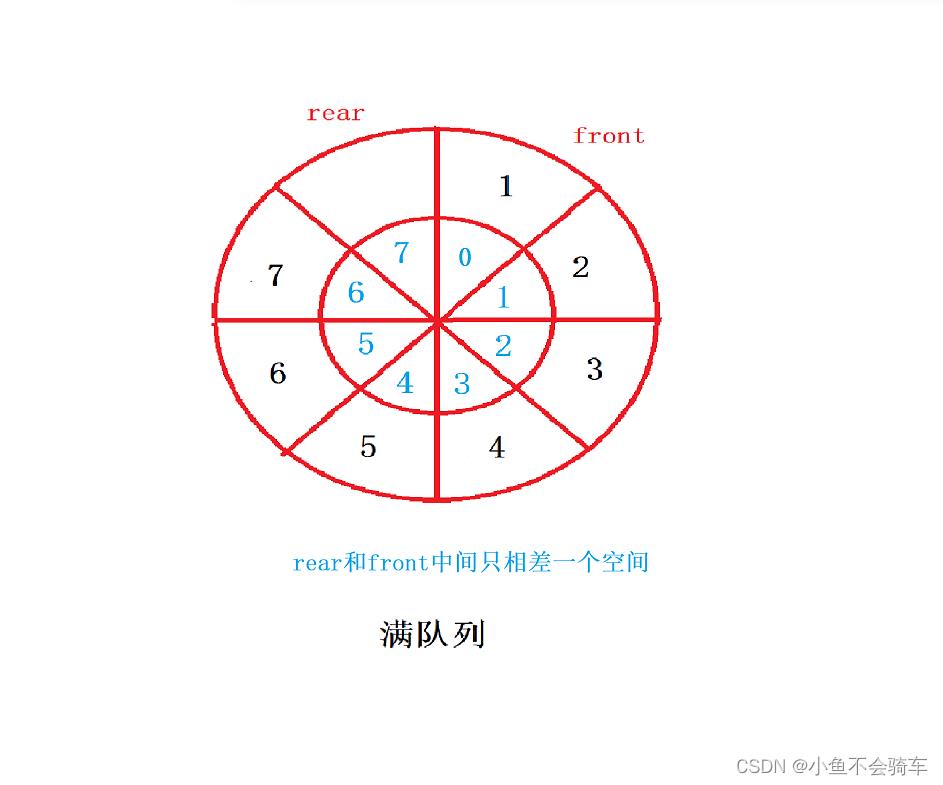
就是当我们的尾指针+1==头指针时(此时的判断不完全正确),说明满了,虽然这样会浪费一个空间,但是对于程序运行的效率和降低书写代码的难度都是有不错的效果的!
正确判满的公式应该是:(rear+1)%array.length==front
上图举例。此时我的rear=7,但是7+1==8并不等于front,但是这个队列明明确确的已经满了,解决方法就是 (rear + 1 ) % 数组长度,当我的rear=7时,(7+1)%8=0,又因为此时的 front=0,所以此时循环队列是满的。
再举个例子:
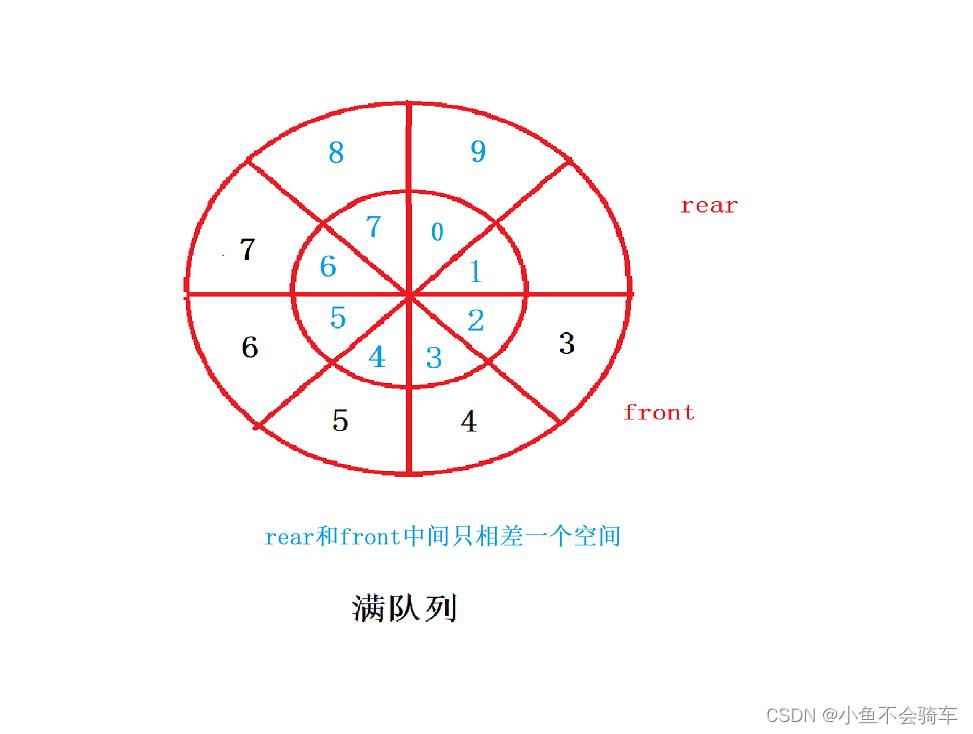
如上图:此时rear=1,并且此时的队列是满的,那我们就套公式(1+1)%8=2,此时front=2,说明队列是满的!
其实%的主要作用就是,每次当我的 rear 为数组最后一个元素的下标时,当他需要再前进一个位置时,便让他重新回到0下标。
判空: rear== front
判满:(rear+1)%array.length == front
求队列长度:上述的公式是 (rear - front + array.length) % array.length
怎么理解呢?依旧是看图,这里分为普通情况和特殊情况
普通情况&特殊情况:
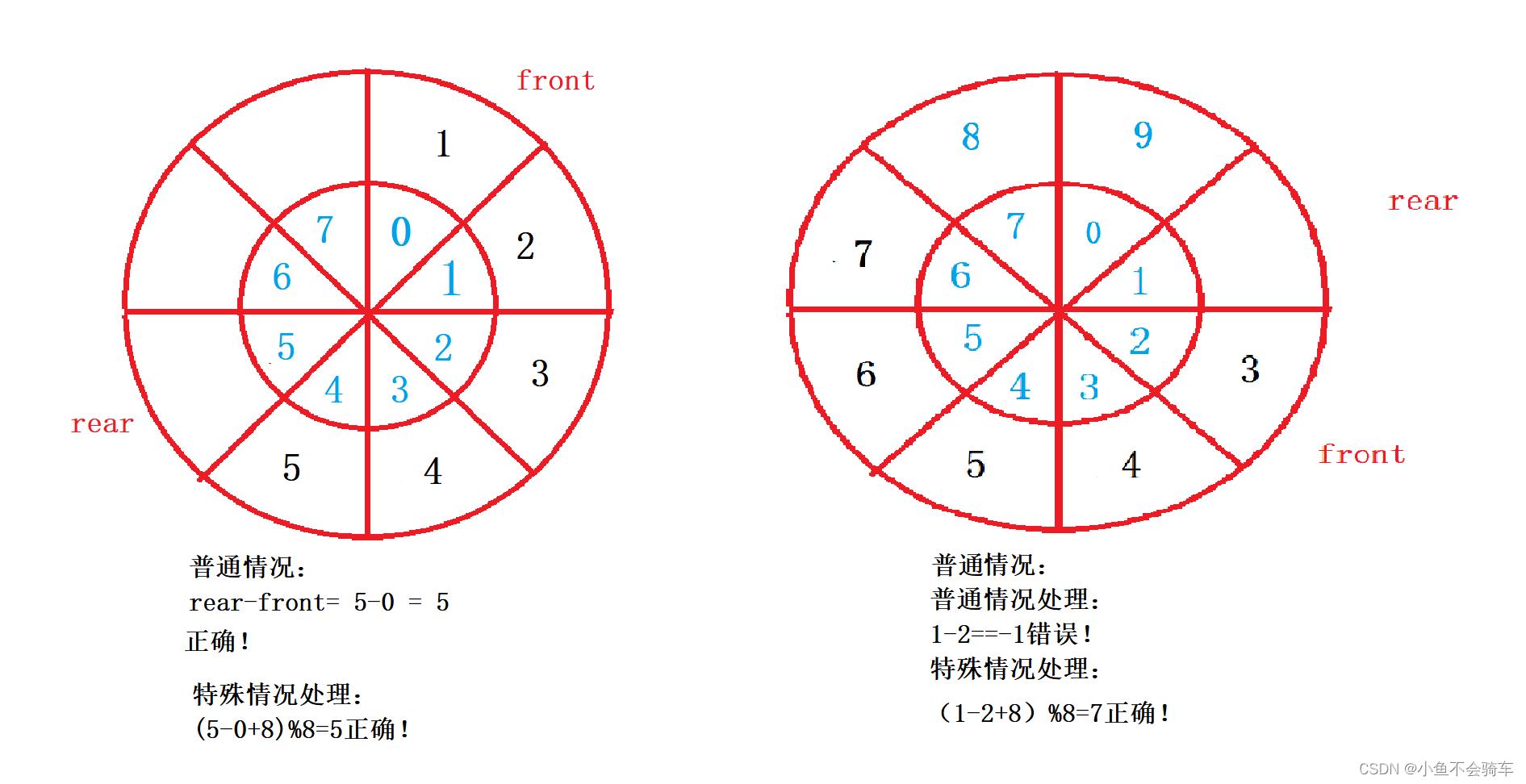
特殊情况指的就是当我的差为负数时,通过 (rear-front+array.length)%array.length 这个公式,对于差是正数时没有影响,但是对于差是负数时,便可以求出正确的元素个数。
3. 循环队列的常见基本算法
(1)循环队列的顺序存储结构
class数据结构之栈和队列熬夜暴肝,有亿点详细
前言
我们之前已经说过线性表那一部分了,今天正式开始栈与队列这部分。这部分用途是十分的广泛,重要程度也是不言而喻的。大家理解性记忆哈,多练习!
栈的很多东西与线性表类似,大家对线性表有什么不了解的可以先去看看我上次写的线性表相信对你能有帮助。
传送门->数据结构之线性表
栈
栈其实就是受限制的线性表,线性表有两种,所以栈按照存储结构来分也有两种。
栈的定义
栈(Stack):只允许在一端进行插入或删除的线性表
栈有两个概念是:栈底和栈顶。一般栈只允许在栈顶进行操作,这样就会让栈有一个特性:后进先出(LIFO)。
栈的基本操作
InitStack(&S):初始化一个空栈S。
StackEmpty(S):判断一个栈是否为空,若栈为空则返回true,否则返回false。
Push(&S, x):进栈,若栈S未满,则将x加入使之成为新栈顶。
Pop(&S, &x):出栈,若栈非空,则弹出栈顶元素,并用x返回。
GetTop(S, &x):读栈顶元素,若栈非空则用x返回栈顶元素。
ClearStack(&S):销毁栈,并释放S占用的内存空间
栈有两种分别是:顺序栈和链栈,接下来我们将它们逐个击破。
顺序栈
顺序栈顾名思义就是采用顺序存储结构的栈
顺序栈的定义为
# define MaxSize 50
typedef struct
ElemType date[MaxSize];
//top用来存放栈顶位置
int top;
SqStack;
栈的一些常用条件
判断栈空:S.top==-1
求栈长:S.top+1
栈满条件:S.top==MaxSize-1
栈的初始化也是非常特殊的,也非常简单,只需要将栈顶位置初始化为-1即可,如下:
void TnitStack (SqStack &S)
S.top=-1;
判断栈空
bool StackEmpty(SqStack S)
if(S.top==-1)
return true;
else
return false;
进栈操作
进栈之前先判断栈是否满了。没有满可以继续存放数据,进栈成功之后返回true。
bool Push(SqStack &S,ElemType x)
if(S.top==MaxSize-1)
return false;
S.date[++S.top]=x;
return true;
出栈操作
出栈之前判断栈中有无元素,没有则不能进行出栈操作,并返回false。
bool Pop(SqStack &s,ElemType &x)
if(S.top==-1)
return false;
x=S.date[S.top--];
return true;
与出栈类似的就是获取栈顶元素,这时候不需要对栈进行改变所以不需要传入栈的引用了,如下:
bool Pop(SqStack S,ElemType &x)
if(S.top==-1)
return false;
x=S.date[S.top];
return true;
共享栈
共享栈就是两个栈公用同一块顺序内存,将两个栈底设置在共享空间的两端,栈顶向空间中间延伸
共享栈与普通栈不同之处就只有判断栈空栈满的条件和栈顶的移动方向,如下:
判空:内存底部栈 top == -1
内存顶部栈 top == MaxSize
栈满:top1-top0 == 1
共享栈的优点是:存取时间复杂度仍为O(1),但空间利用更加有效
其实所谓的进栈出栈,原来的元素还在存储空间上,只不过,每次都是把他们覆盖了而已,我们只通过栈顶位置来判断,来限制定义操作这个栈,可见栈顶(top)移动的重要性。
链栈
链栈就是采用链式存储的栈,有栈顶结点与栈低结点
链栈的定义
链栈的定义与链表定义几乎相同,它们唯一的不同之处就是在操作上了
typedef struct Linknode
ElemType date;
Struct Linknode *next;
*LiStack;
链栈所有操作都与链表相同这里就不一一罗列了,对链表不了解的可以先去看看数据结构之线性表。链栈与链表唯一一点不同的是栈的所有操作都只能在表头进行。
类似于入栈操作就是头插法,包括出栈之类的操作也只能在头部进行操作。
队列
队列的定义
队列(Queue) 只允许在表的一端进行插入,表的另一端进行删除操作的线性表,它的特性是先进先出(FIFO)
队列的基本操作
InitQueue(&Q):初始化队列,构造一个空队列Q。
QueueEmpty(Q):判队列空,若队列Q为空返回 true,否则返回false。
EnQueue(&Q, x):入队,若队列Q未满,则将x加入使之成为新的队尾。
DeQueue(&Q, &x):出队,若队列Q非空,则删除队头元素,并用x返回。
GetHead(Q, &x):读队头元素,若队列Q非空则用x返回队头元素。
ClearQueue(&Q):销毁队列,并释放队列Q占用的内存空间
队列根据存储结构也分为:顺序队列与链式队列。
顺序队列
所谓顺序队列就是采用顺序结构队列,它由一个数组和一个队头位置标记和一个队尾位置标记组成。
代码实现为:
# define MaxSize 50
typedef struct
ElemType date[MaxSize];
int front,rear;
SqQueue;
front一般指向队头元素,rear一般指向队尾元素的下一位置。也可以front指向队头元素的前一位置,rear指向队尾元素。两种指向位置不同对应操作也不同,但是我们一般用前者,今天也是讲解前者。
我们插入元素时候是从队尾进入队列,从队头离开队列。
常用判断条件(传入队列为Q)
判断队空条件:Q.front==Q.rear
求队长:Q.rear-Q.front
判断队满条件:Q.rear==MaxSize
但是这里的判断队满条件是有问题的,试想如果队列都存满了即:Q.rear==MaxSize的时候队头出删除了一个元素,这时候队头指针会下移,并且空出来了一个队列位置,但是它依旧满足Q.rear==MaxSize判断队满的条件,这样就会出现假溢出问题了。
为了解决这个问题,我们请出今天队列的主角——循环队列,为什么说它是主角呢,因为我们用队列时候一般都用它!!
循环队列
首先要清楚循环队列只是逻辑上的循环,在内存上依然是顺序存储的,所以它仍然属于顺序队列。
那它是如何实现逻辑上的循环呢?
它把队列的尾部与首部在逻辑上连接起来了,即:当rear存储了最后一个元素位置的元素后直接跳到下标为0处。
如果队列没有移除元素,那么front就在下标为0处(即队头前无空数组),这时候rear与front就在同一个位置即:Q.front==Q.rear,此时队满。
如果队列移除了元素那么front就在下标不为0处(即队头前有空数组),这时还能向队列中加入元素,直至Q.front==Q.rear时,队列才满。
那它是怎么实现从最后位置到起始位置的呢?,,它依靠**取余%(MaxSize)**实现。
使用取余后,队列的front,rear,指针移动与求队列长度就都发生变化了,如下:
front指针移动:
Q.front = (Q.front + 1) % MaxSize
rear指针移动:
Q.rear = (Q.rear + 1) % MaxSize
队列长度:
(Q.rear + MaxSize - Q.front) % MaxSize
大家注意体会,可以自己画图试试指针的移动。
但是这时候问题又来了,如果你前面的都明白了,那你会发现现在判断队空与队满的条件一样了,都等于Q.front==Q.rear
很显然这样并不行,我们就得想办法改变其中之一的条件了,我们一般改变的是队满的判断条件,使得它们不一样。
方案一:
牺牲一个存储单元
就是最后一个存储单位不存放元素,这时候:
队空条件:Q.front==Q.rear
队满条件:Q.front==(Q.rear+1) %MaxSize
方案二:
增加一个变量代表元素的个数
就是在定义队列时候增加一个变量size来监控队列中存储元素的数量。这时候:
队空条件:Q.size== 0
队满条件:Q.size == MaxSize
还有其他的方案,大家主要还是根据场景变化来改变。
不过我们一般用的都是方案一,下面例子都是使用方案一实现的。
入队操作
bool EnQueue(SqQueue &Q,ElemType x)
if(Q.front==(Q.rear+1)%MaxSize)
return false;
Q.date[Q.rear]=x;
Q.rear = (Q.rear + 1) % MaxSize;
return true;
出队操作
bool DeQueue(SqQueue &Q,ElemType &x)
if(Q.rear == Q.front)
return false;
x=Q.date[Q.front];
Q.front = (Q.front+1)%MaxSize;
return true;
链式队列
链队就是采用链式存储的队列,它包括结点,一个头指针和一个尾指针。结点与链表定义的结点是相同的包括一个数据域和一个指针域。如下:
定义链队
typedef struct
ElemType date;
struct LinkNode *next;
LinkNode;
typedef struct
LinkNode *front, *rear;
LinkQueue;
初始化链队
我们初始化的链表一般都是带头结点的链表,这样的好处我在线性表那节,已经说过了这里不做解释。
同时这里的链队也都是带头结点的
void InitQueue(LinkQueue &Q)
Q.front = (LinkNode*)malloc(sizeof(LinkNode));
Q,rear = Q.front;
Q.front->next=NULL;
判断队空
bool isEmpty(LinkQueue Q)
if(Q.front == Q.rear)
return true;
else
return false;
入队操作
链队也是动态的所以不用怕队满,所以不需要判断队是否满了
void EnQueue(LinkQueue &Q,ElemType x)
LinkNode *s = (LinkNode*)malloc(sizeof(LinkNode));
s->date=x;
s->next=NULL;
Q->rear->next=s;
Q.rear=s;
出队操作
bool DeQueue(LinkQueue &Q,ElemType &x)
if(Q.rear==Q.front)
return false;
LinkNode *p=Q.front->next;
x=p->date;
Q.front->next=p->next;
if(Q.rear==p)
Q.rear=Q.front;
free(p);
return true;
这里需要说明一下的就是这个if的判断语句是如果队列中只有一个元素在出队后,队中就没有元素了,此时应该Q.rear=Q.front
栈与队列的应用
在讲完栈与队列基础的东西之后我们就到有难度也是最实用的一个模块了,在讲应用之前先说一下它们各自的一些升华的知识。
栈与队列输入输出
在栈与队列中分别依次输入1,2,3,4它们的输出序列是什么呢?
在队列中输出序列必定是1,2,3,4因为它是先进先出嘛
但是栈中就不一定了。。
如果是连续的输入与输出,那么栈输出的必然是4,3,2,1这也没有什么可以争论的,但是如果输入输出是不连续的就一定是这个答案了
假设1先入栈,然后1立马就出栈了然后其他的数据也有变化,那么情况就很多很多了。
对1,2,3,4组合排列可得:
1234 1243 1324 1342 1423 1432
2134 2143 2314 2341 2413 2431
3124 3142 3214 3241 3412 3421
4123 4132 4213 4231 4312 4321
一共有24种,那么这24都可以作为栈的输出序列吗?
并不是,有些是不合法的。
譬如说4123
想要4先出栈,那么入栈顺序必定是1,2,3,4如果4先出栈,那么接下来肯定是3,2,1依次出栈了。
那么如果需要找到不合法的出栈序列这么多种我们要一个一个试吗?
不需要我们有一个准则,如果不符合这个准则那么就必然是不合法的出栈顺序
准则:出栈序列中每一个元素后面所有比它小的元素组成一个递减序列
有多少种出栈序列我们有一个公式可以算出来,如下:
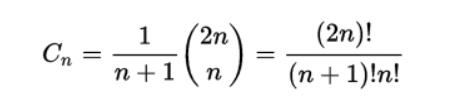
如果你想知道公式来由,你可以去出栈序列看看
双端队列
双端队列允许两端都可以进行入队以及出队操作的队列
之前我们学习的队列是容许在一端输入另一端输出,而双端队列是允许在两端都可以进行输入输出的,我愿称之为队列最强变异版。
其实在仔细一想你会发现这是两个栈拼接到一起了,只不过是屁股对着屁股而已
但是无论它怎么变化它总是先出的元素在前,后出的元素在序列后
还有两种是受限制的双端队列,一种是只允许一端输出,两端输入还有一种是只允许一段输入,两端输出。
双端队列可以实现栈输出序列不合法的序列,受限制的双端序列可以实现部分栈输出序列不合法的序列
这部分,没什么好说的,用的也不多大家知道了就好了。接下来我们说一下栈与队列的一些常用应用。
栈的应用
学习了栈你可能会觉得这东西没什么用,但是栈的用处十分庞大,我们经常会用它去解决各种问题,今天就来简单列举两个吧!
表达式求值
我们对于表达式有三种定义分别是:前缀表达式,中缀表达式,后缀表达式
所谓中缀表达式就是我们平时都在用的譬如:A+B
对于这个表达式把他转换为前缀表达式就是+AB,也就是运算符号放到前面
那么后缀表达式就是:AB+
我们在很多时候都会对三种表达式之间进行相互转换,我们可以手动进行转换,那么有没有办法我们通过程序编写出来呢?
当然可以,而且就用队列就可以,算法思想如下:
中缀表达式转换为后缀表达式算法思想
数字直接加入后缀表达式
运算符时:
a. 若为’(’ ,入栈;
b. 若为’)’,则依次把栈中的运算符加入后缀表达 式,直到出现’(’,并从栈中删除’(’;
c. 若为’+’,’-’,’*’,’/’,
· 栈空,入栈;
· 栈顶元素为’(’,入栈;
· 高于栈顶元素优先级,入栈;
· 否则,依次弹出栈顶运算符,直到一个优先级比 它低的运算符或’('为止;
d. 遍历完成,若栈非空依次弹出所有元素
同样我们也可以把后缀表达式转换为中缀表达式,如下:
算法思想:
顺序扫描后缀序列
· 若是数字压入栈中;
· 若是操作符,连续弹出栈中两个元素,按操作符计算并把结果压入栈中。
· 扫描完毕后栈顶为最后结果
你可以对一个式子进行,这个流程看能不能成功转换
括号匹配
大家都知道括号是成对存在的,那么怎么知道一堆括号序列中是否合法呢?
我们仍然使用队列算法,如下
算法思想:
1)初始一个空栈,顺序读入括号。
2)若是右括号,则与栈顶元素进行匹配
· 若匹配,则弹出栈顶元素并进行下一个元素
· 若不匹配,则该序列不合法
3)若是左括号,则压入栈中
4)若全部元素遍历完毕,栈中非空则序列不合法
递归
递归 :若在一个函数、过程或数据结构的定义中又应用了它自身,则称它为递归定义的,简称递归
一个完整的递归由两部分构成:递归表达式和递归出口
最简单的递归莫过于斐波那契数了,看看它的结构:
int Fib(int n)
if(n==0)
return 0;
else if(n==1)
return 1;
else
return Fib(n-1)+Fib(n-2);
这个里面递归表达式就是Fib(n-1)+Fib(n-2),递归出口就是n等于1或者0时候
递归的精髓在于能否将原始问题转换为属性相同但规模较小的问题
那么递归哪里用到栈了呢?
· 在递归调用过程中,系统为每一层的返回点、局部变量、传入实参等开辟 了递归工作栈来进行数据存储,递归次数过多容易造成栈溢出
但是递归往往计算效率不高,就比如说这个斐波那契数吧,它在计算时有很多重复的数字依然在继续调用递归计算,比如Fib(2)它就得算好多次
递归对于栈运用还有:递归转换算法转换为非递归算法,往往需要借助栈来进行
因为这里主要是说栈的运用所以对递归就不深入解析,等后期会专门出一期递归算法的!
结语
栈与队列也是很简单的数据结构,相信大家只要用脑袋去思考,必然能够轻松的凯瑞它!
有问题欢迎指正!感谢~
坚持与努力,下一节是串,数组和广义表!
持续更新中…
以上是关于数据结构:栈和队列(详细讲解)的主要内容,如果未能解决你的问题,请参考以下文章
