排序算法——插入排序
Posted 心皿月
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了排序算法——插入排序相关的知识,希望对你有一定的参考价值。
目录
🎨基本介绍
插入式排序属于内部排序法,是对待排序的元素以插入的方式寻找该元素的适当位置,以达到排序的目的。
🎹算法思想
插入排序(Insertion Sorting)的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,在有序表中从后往前进行比较,将它插入到有序表中的适当位置,使之成为新的有序表。
🏸实例
将101,34,119,1进行从小→大的排序
🎠思路分析
101,34,119,1
第一趟:此时有序表为101,无序表为:34,119,1
从后往前遍历有序表,将34和101进行比较,34<101,此时将101后移一个位置。此时已经遍历完有序表中的所有元素,故将34插入在101的前面,即有序表的第一个位置,得到新的有序表:34,101
34,101,119,1
第二趟:从后往前遍历有序表,将119与34和101进行比较,发现119均大于两者。故将119直接插在101后面,即有序表的最后一个位置,得到新的有序表:34,101,119
34,101,119,1
第三趟:从后往前扫描有序表,1<119,故将119往后移一个位置;1<101,将101往后移一个位置;1<34,将34往后移一个位置。此时已经遍历完有序表中的所有元素,故将1插入在34的前面,即有序表的第一个位置。
此时所有元素已经完全有序:1,34,101,119
🪁代码实现
public static void main(String[] args)
int []arr=101,34,119,1;
insertSort(arr);
System.out.println("排序后的数组为:"+Arrays.toString(arr));
public static void insertSort(int[]arr)
if (arr==null||arr.length==1)
return;
//从第二个元素开始,和前面的有序表进行比较
for (int i=1;i<arr.length;i++)
int temp=arr[i];//记录要插入的值,将待插入的值取出并保存在temp中,防止数据移动时该元素丢失
int j=i-1;
//从后往前进行遍历比较
for (;j>=0;j--)
if (arr[j]>temp)
arr[j+1]=arr[j];//后移一个位置
else
arr[j+1]=temp;//直接将待插入的元素,插入在有序表的尾部
break;
arr[j+1]=temp;//遍历完有序表所有大于temp的元素后,将temp插入
实现结果:
🛹算法性能分析
🚀时间复杂度
最坏情况:当待排序序列为逆序状态,首先遍历整个序列,之后一个一个地将待插入元素放在已排好序的序列最前面,之后的所有元素都需要向后移动一位,时间复杂度为O(n^2)
最好情况:当待排序序列为正序状态,则遍历完整个序列,当插入元素时,只比较一次就够了,所以时间复杂度为O(n)
平均情况:当被插入的元素放在已排序的序列中间位置时,为平均情况,比较和移动的时间复杂度为O(n/2),所以总的时间复杂度依然为O(n^2)
🛴空间复杂度
空间复杂度为O(1)
🛸稳定性
当待插入元素与有序序列中比较的元素相等时,将待插入元素直接插入在该相等元素的后面。所以,两个元素位置的前后顺序没有改变,故插入排序是稳定的
算法排序算法之插入排序
在前一篇中,我们已经对冒泡排序做了解析说明,本节我们将继续对排序算法(插入排序)进行相关解析说明。
一、排序算法系列目录说明
冒泡排序(Bubble Sort)
插入排序(Insertion Sort)
希尔排序(Shell Sort)
选择排序(Selection Sort)
快速排序(Quick Sort)
归并排序(Merge Sort)
堆排序(Heap Sort)
计数排序(Counting Sort)
桶排序(Bucket Sort)
基数排序(Radix Sort)
二、插入排序(Insertion Sort)
插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。打过扑克牌的应该都会明白(当然,如果你说你打扑克牌摸牌的时候从来不按牌的大小整理牌,那我只能呵呵了)
1.基本思想
插入排序的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
趣味解释:
插入排序操作类似于摸牌并将其从大到小排列。每次摸到一张牌后,根据其点数插入到确切位置。
如上图:表示的是摸到草花7后进行插入的过程。忽略最右边的草花10,相当于一开始7在最右边,然后逐个与左边的牌相比较(当然左边的牌早已排好顺序),将其放置在合适的位置。当摸到草花10后重复上述过程即可。
而实际中,如何将插入牌的这个过程应用到实际排序操作中呢?具体我们以一组数字来说操作说明:
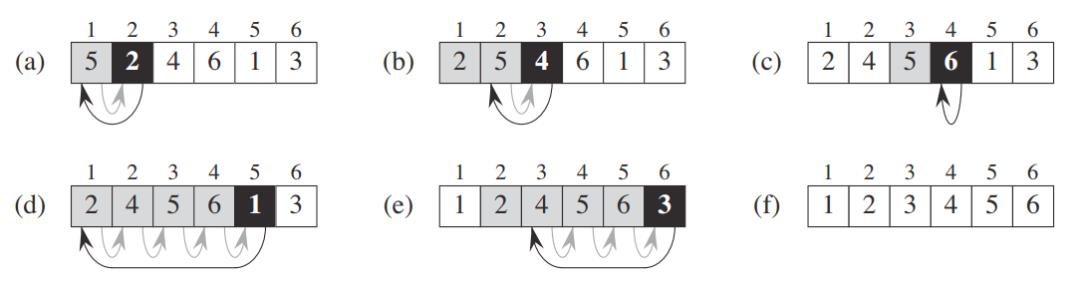
例如我们有一组数字:{5,2,4,6,1,3},我们要将这组数字从小到大进行排列。我们从第二个数字开始,将其认为是新增加的数字,这样第二个数字只需与其左边的第一个数字比较后排好序;在第三个数字,认为前两个已经排好序的数字为手里整理好的牌,那么只需将第三个数字与前两个数字比较即可;以此类推,直到最后一个数字与前面的所有数字比较结束,插入排序完成。
2.实现逻辑
① 从第一个元素开始,该元素可以认为已经被排序
② 取出下一个元素,在已经排序的元素序列中从后向前扫描
③如果该元素(已排序)大于新元素,将该元素移到下一位置
④ 重复步骤③,直到找到已排序的元素小于或者等于新元素的位置
⑤将新元素插入到该位置后
⑥ 重复步骤②~⑤
3.动图演示
4.性能分析
平均时间复杂度:O(N^2)
最差时间复杂度:O(N^2)
空间复杂度:O(1)
排序方式:In-place
稳定性:稳定
如果插入排序的目标是把n个元素的序列升序排列,那么采用插入排序存在最好情况和最坏情况:
(1) 最好情况:序列已经是升序排列,在这种情况下,需要进行的比较操作需(n-1)次即可。
(2) 最坏情况:序列是降序排列,那么此时需要进行的比较共有n(n-1)/2次。
插入排序的赋值操作是比较操作的次数减去(n-1)次。平均来说插入排序算法复杂度为O(N^2)。
最优的空间复杂度为开始元素已排序,则空间复杂度为 0;
最差的空间复杂度为开始元素为逆排序,则空间复杂度最坏时为 O(N);
平均的空间复杂度为O(1)
注:
n:数据规模
k:”桶”的个数
In-place:占用常数内存,不占用额外内存
Out-place:占用额外内存
5.代码实现
// 插入排序(C++)
void InsertSort(int arr[], int len){
// 检查数据合法性
if(arr == NULL || len <= 0){
return;
}
for(int i = 1; i < len; i++){
int tmp = arr[i];
int j;
for(j = i-1; j >= 0; j--){
//如果比tmp大把值往后移动一位
if(arr[j] > tmp){
arr[j+1] = arr[j];
}
else{
break;
}
}
arr[j+1] = tmp;
}
}
6.算法优化改进
6.1 改进方法①
场景分析:直接插入排序每次往前插入时,是按顺序依次往前查找,数据量较大时,必然比较耗时,效率低。
改进思路:在往前找合适的插入位置时采用二分查找的方式,即折半插入。
二分插入排序相对直接插入排序而言:平均性能更快,时间复杂度降至O(NlogN),排序是稳定的,但排序的比较次数与初始序列无关,相比直接插入排序,在速度上有一定提升。逻辑步骤:
① 从第一个元素开始,该元素可以认为已经被排序
② 取出下一个元素,在已经排序的元素序列中二分查找到第一个比它大的数的位置
③将新元素插入到该位置后
④ 重复上述两步
改进代码:
// 插入排序改进:二分插入排序(C++)
void BinaryInsertSort(int arr[], int len)
{
int key, left, right, middle;
for (int i=1; i<len; i++)
{
key = a[i];
left = 0;
right = i-1;
while (left<=right)
{
middle = (left+right)/2;
if (a[middle]>key)
right = middle-1;
else
left = middle+1;
}
for(int j=i-1; j>=left; j--)
{
a[j+1] = a[j];
}
a[left] = key;
}
}
6.2 改进方法②
场景分析:(1) 插入排序对几乎已排好序的数据操作时,效率很高,可以达到线性排序的效率。(2) 插入排序在每次往前插入时只能将数据移动一位,效率比较低。
改进思路:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。
改进思路二的方法实际上就是希尔排序。在这里只给出思路,在后续系列《【算法】排序算法之希尔排序》中再做具体讲解说明。
三、总结
插入排序不适合对于数据量比较大的排序应用。但是,如果需要排序的数据量很小,例如,量级小于千,那么插入排序还是一个不错的选择。尤其当数据基本有序时,采用插入排序可以明显减少数据交换和数据移动次数,进而提升排序效率。在STL的sort算法和stdlib的qsort算法中,都将插入排序作为快速排序的补充,用于少量元素的排序。
以上是关于排序算法——插入排序的主要内容,如果未能解决你的问题,请参考以下文章
数据结构之排序算法Java实现—— 插入类排序之折半插入排序算法