深度学习：《PyTorch入门到项目实战》第九天：Dropout实现（含源码）

Posted 2022-06-01 JoJo的数据分析历险记

【深度学习】：《PyTorch入门到项目实战》第九天:Dropout实现

• ✨本文收录于【深度学习】：《PyTorch入门到项目实战》专栏，此专栏主要记录如何使用PyTorch实现深度学习笔记，尽量坚持每周持续更新，欢迎大家订阅！
• 🌸个人主页：JoJo的数据分析历险记
• 📝个人介绍：小编大四统计在读，目前保研到统计学top3高校继续攻读统计研究生
• 💌如果文章对你有帮助，欢迎✌关注、👍点赞、✌收藏、👍订阅专栏

参考资料：本专栏主要以沐神《动手学深度学习》为学习资料，记录自己的学习笔记，能力有限，如有错误，欢迎大家指正。同时沐神上传了的教学视频和教材，大家可以前往学习。

• 视频：动手学深度学习
• 教材：动手学深度学习

文章目录

• 【深度学习】：《PyTorch入门到项目实战》第九天:Dropout实现
• 写在前面
• 1. Dropout理论基础
• • 1.1 基本原理
  • 1.2 具体实施
• 2. 代码实现
• • 2.1 dropout层定义
  • 2.2初始化参数
  • 2.3 模型定义
  • 2.4 模型训练
  • 2.5 简洁代码实现
• 3.总结

写在前面

上一章我们介绍了L2正则化和权重衰退，在深度学习中，还有一个很实用的方法——Dropout，能够减少过拟合问题。之前我们介绍了我们的目的是要训练一种泛化的模型，那么就要求模型的鲁棒性较强。一个还不错的尝试是在训练神经网络时，让模型的结果不那么依赖某个神经元，因此在训练神经网络过程中，我们每次迭代将隐藏层的一些神经元随机丢弃掉，这样就不会使得我们的模型太依赖某一个神经元，从而使得我们的模型在未知的数据集上或许会有更好的泛化能力。下面我们具体来看dropout的原理。

1. Dropout理论基础

1.1 基本原理

假设我们要训练的神经网络如下所示：

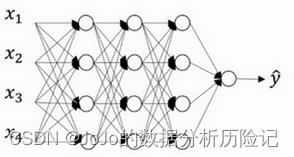
传统的神经网络是全连接的，也就是每一个神经元都会与下一个神经元连接，而dropout会遍历每一层神经网络，设置神经元消除的概率，然后消除一定比例的神经元和它的进出的连线，从而能够得到一个规模更小的神经网络。 假设每一层消除神经元的概率是0.5，在一次训练迭代中，消除的神经元如下所示：

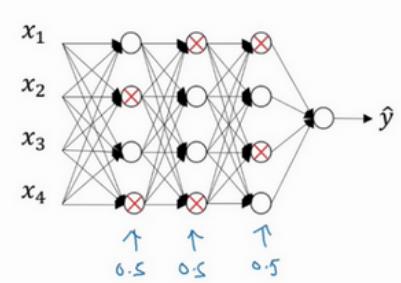
以第一层为例，第二个神经元和第四个神经元消除了，那么其节点及进出的连线全部消除，得到消除后的神经网络如下：

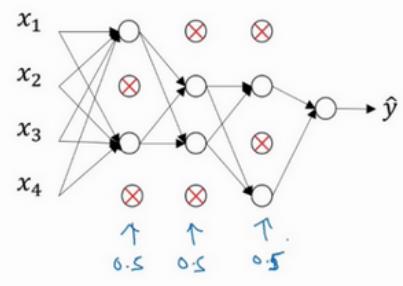
可以看出dropout得到了一个更简洁的神经网络。对于每一个训练样本，我们都以dropout之后的神经网络进行训练，这样使得我们的训练样本不会依赖于某个特征。

1.2 具体实施

在具体实施dropout时，我们介绍最常用的反向随机失活。首先我们需要定义一个随机向量，如果小于丢弃率p，则权重设为0，相当于将这个神经元丢弃。然后对中间值向外扩展，除以1-p，以保障期望不变。具体思想如下：假设在第某一层隐藏层我们有50个神经元，丢弃率为0.2，也就是有10个神经元被归0（丢弃）了，那么我们中间值的期望减少了20%，为了不影响中间值的期望，我们除以1-p来保证其期望不变。具体公式如下
$$a^{\prime }=\begin{array}{l}0,\text{ p}\\ \frac{a}{1-p},\text{ 1-p}\end{array}$$
此时$E(a^{\prime })=a$。从这里我们也可以发现，dropout是通过设置权重为0来实现消除神经元，并不是直接将神经元个数减少删除。下面我们来看看具体代码实现部分

2. 代码实现

2.1 dropout层定义

"""导入相关库"""
import torch
from torch import nn
from d2l import torch as d2l
"""定义dropout函数"""
def dropout_layer(X, dropout):
    '''
    实现丢弃
    '''
    assert 0 <= dropout <= 1#断言，确保dropout在0-1之间
    # dropout=1，所有元素都被丢弃
    if dropout == 1:
        return torch.zeros_like(X)
    # dropou=0，所有元素都被保留
    if dropout == 0:
        return X
    # 其他情况，dropout在0-1之间
    mask = (torch.rand(X.shape) > dropout).float()#返回0和1的向量
    return mask * X / (1.0 - dropout)#进行中间值拓展

通过上面定义的dropout_layer函数，我们下面以一个具体的小例子来测试一下

X= torch.arange(8, dtype = torch.float32).reshape((2, 4))# 定义一个张量
print(X)#不进行dropout情况
print(dropout_layer(X, 0.))#dropout为0
print(dropout_layer(X, 0.5))#dropout为0.5
print(dropout_layer(X, 1.))#dropout为1

tensor([[0., 1., 2., 3.],
        [4., 5., 6., 7.]])
tensor([[0., 1., 2., 3.],
        [4., 5., 6., 7.]])
tensor([[ 0.,  2.,  4.,  0.],
        [ 8., 10.,  0.,  0.]])
tensor([[0., 0., 0., 0.],
        [0., 0., 0., 0.]])

2.2初始化参数

# 使用之前的fasion_mnist数据集图像，设置具有两个隐藏层的神经网络
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256

这是一个具有两个隐藏层的神经网络，结构如下（具体神经元个数不同）：

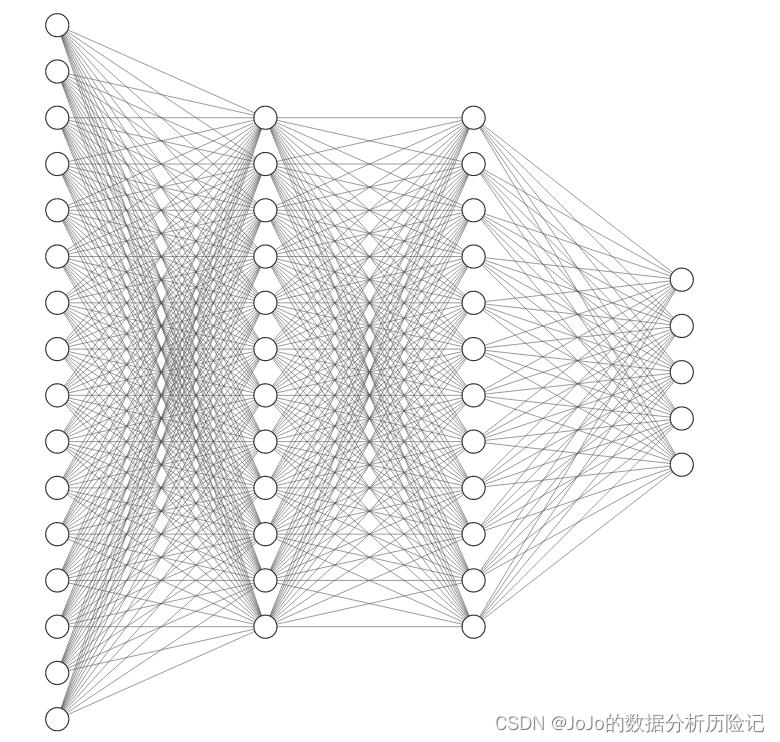
2.3 模型定义

使用dropout定义在每个隐藏层的输出中，其中不同层的p设置不同。一个比较常用的做法是：越接近输入层的，p设置的越小。因为一开始我们不希望输入信息丢失太多，因此该模型的结构是 ：

linear--Relu--dropout--linear--Relu--dropout--linear

下面我们来看看具体代码是如何实现的，假设第一层dropout的概率为0.2，第二层为0.5

dropout1, dropout2 = 0.2, 0.5

class Net(nn.Module):
    def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,
                 is_training = True):
        super(Net, self).__init__()
        self.num_inputs = num_inputs
        self.training = is_training
        self.lin1 = nn.Linear(num_inputs, num_hiddens1)#定义线性层
        self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
        self.lin3 = nn.Linear(num_hiddens2, num_outputs)
        self.relu = nn.ReLU()#定义Relu激活函数

    def forward(self, X):
        H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
        # 只有在训练模型时才使用dropout
        if self.training == True:
            # 在第一个全连接层之后添加一个dropout层
            H1 = dropout_layer(H1, dropout1)
        H2 = self.relu(self.lin2(H1))
        if self.training == True:
            # 在第二个全连接层之后添加一个dropout层
            H2 = dropout_layer(H2, dropout2)
        out = self.lin3(H2)
        return out
        #在这里没有定义softmax回归，因为在定义损失函数时，CrossEntropyLoss会自动计算softmax

net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)

2.4 模型训练

num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

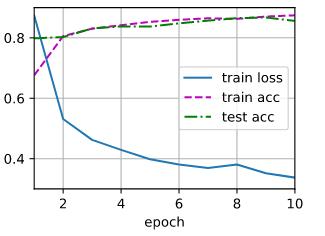
2.5 简洁代码实现

下面我们使用nn内置方法来实现dropout的神经网络.神经网络的结构如下： linear-relu-dropout-linear-dropout-relu-linear

"""
构建神经网络
"""
net = nn.Sequential(nn.Flatten(),
        nn.Linear(784, 256),
        nn.ReLU(),
        # 在第一个全连接层之后添加一个dropout层
        nn.Dropout(dropout1),
        nn.Linear(256, 256),
        nn.ReLU(),
        # 在第二个全连接层之后添加一个dropout层
        nn.Dropout(dropout2),
        nn.Linear(256, 10))
"""
初始化权重
"""
def init_weights(m):
    if type(m) == nn.Linear:
        """对于线性层，使用正态分布初始化权重"""
        nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights)

trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

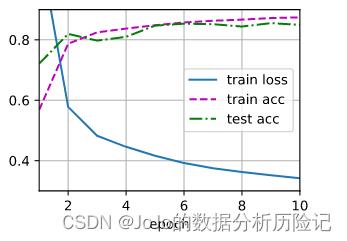
3.总结

• 1.dropout有效的原理，直观上理解：不要依赖于任何一个特征，因为该单元的输入可能随时被清除，或者说该单元的输入也都可能被随机清除。因此我们不愿意把所有赌注都放在一个节点上，不愿意给任何一个输入加上太多权重，因为它可能会被删除，因此该单元将通过这种方式积极地传播开，并为单元的每个输入增加一点权重，通过传播所有权重，dropout将产生收缩权重的平方范数的效果。
• 2.dropout一大缺点就是没有明确的损失函数，每次迭代，都会随机移除一些节点，如果再三检查梯度下降的性能，实际上是很难进行复查的，因为我们没有定义明确的损失函数。
• 3.dropout只在训练集上进行，而不在测试集上使用。 因为在测试阶段进行预测时，我们不期望输出结果是随机的，如果测试阶段应用dropout函数，预测会受到干扰。