Python第三方库之MedPy

Posted 2023-03-30 Albert Darren

文章目录

• 1.MedPy简介
• 2.MedPy安装
• 3.MedPy常用函数
• • 3.1 `medpy.io.load(image)`
  • 3.2 `medpy.metric.binary.dc(result, reference)`
  • 3.3 `medpy.metric.binary.jc(result, reference)`
  • 3.4 `medpy.metric.binary.hd(result,reference,voxelspacing=None,connectivity=1,)`
  • 3.5 `medpy.metric.binary.hd95(result,reference,voxelspacing=None,connectivity=1,)`
  • 3.6 `medpy.metric.binary.recall(result, reference)`
  • 3.7 `medpy.metric.binary.sensitivity(result, reference)`
  • 3.8`medpy.metric.binary.true_positive_rate(result, reference)`
  • 3.9`medpy.metric.binary.specificity(result, reference)`
  • 3.10`medpy.metric.binary.true_negative_rate(result, reference)`
  • 3.11`medpy.metric.binary.precision(result, reference)`
  • 3.12 `medpy.metric.binary.positive_predictive_value(result, reference)`
  • 3.13 `medpy.io.save(arr, filename, hdr=False, force=True, use_compression=False)`
• 4.参考文献

1.MedPy简介

MedPy 是一个图像处理库和针对医学(如高维)图像处理的脚本集合，此处主要讨论利用该库计算常见的医学图像分割任务评价指标，如Dice、Jaccard、Hausdorff Distance、Sensitivity、Specificity、Positive predictive value等。

论文表格的表头一般使用评价指标的英文全称首字母大写简写，如PPV代表阳性预测值，故此处也给出。

• Dice相似系数(Dice Similarity Coefficient，DSC)或Dice系数(Dice Coefficient，DC)

  也称为索伦森-骰子系数是用于衡量两个样本相似性的统计量。它是由植物学家Thorvald Sørensen和Lee Raymond Dice独立开发的，他们分别于1948年和1945年发表。是最常用的一项评价指标，用于有效衡量分割算法预测标签与真实标注标签的空间重叠程度，其对应值越大表示分割精度越高。该指标最初应用于离散数据，给定两个集合A 和B，则定义为两个集合共有的元素数除以每个集合中元素数之和的两倍
  $$DSC=\frac{2|A\cap B|}{|A|+|B|}$$
  其中，$|A|$和$|B|$是两个集合的基数（即每个集合中的元素数)

  当应用于布尔数据时，使用真阳性 (TP)、假阳性(FP) 和假阴性(FN) 的定义，它可以写为
  $$DSC=\frac{2TP}{2TP+FP+FN}$$

• Jaccard相似系数(Jaccard Similarity Coefficient，JSC)或Jaccard系数(Jaccard Coefficient，JC)

  与 Dice 相似系数指标相似，也是一种衡量两幅图像相似程度的指标，其由实际分割结果与真实标签的交集同二者并集的比值得出，反映了分割方法的准确程度，其值越高，分割结果越准确。设TP表示正确预测为正例的数量，FP表示错误预测为正例的数量，FN表示错误预测为反例的数量，则定义为

  $$\text{ Jaccard}=\frac{TP}{TP+FP+FN}$$

• 豪斯多夫距离(Hausdorff distance，HD)

  表示预测分割区域边界与真实肿瘤区域边界之间的最大距离，其值越小代表脑肿瘤边界分割误差越小、质量越好。设 X 和 Y 是度量空间$(M,d)$的两个非空子集，则定义他们的Hausdorff distance $d_H(X,Y)$为
  $$d_H(X,Y)=\max d_{XY},d_{YX}=\max \underset{x\in X}{\max }\underset{y\in Y}{\min }d(x,y),\underset{y\in Y}{\max }\underset{x\in X}{\min }d(x,y)$$
  计算绿色曲线 X 和蓝色曲线 Y 之间的豪斯多夫距离的分量过程如下图所示。

  首先，对点集X中的每一个点$x$计算其到点集Y中的每一个点$y$的距离，保留最短距离${\inf }_{x\in X}d(x,y)$，然后找出保留的最短距离中的最大距离${\sup }_{y\in Y}{\inf }_{x\in X}d(x,y)$记为$d_{XY}$。然后，对点集Y中的每一个点$y$计算其到点集X中的每一个点$x$的距离，保留最短距离${\inf }_{y\in Y}d(x,y)$，然后找出保留的最短距离中的最大距离${\sup }_{x\in X}{\inf }_{y\in Y}d(x,y)$记为$d_{YX}$。最后，取$d_{XY}$和$d_{YX}$最大值作为点集X和Y之间的豪斯多夫距离。

• 95％ 豪斯多夫距离(95％ Hausdorff distance，HD95)

  为了排除一些离群点造成的不合理距离，保持整体数值稳定性，一般选择从小到大排名前 95%的距离作为实际豪斯多夫距离，称之为 95% 豪斯多夫距离。

• 灵敏度(Sensitivity)

  也称真阳性率(True Positive Rate)、命中率(hit rate)和召回率(Recall)，表示预测为正的肿瘤标签占真实肿瘤标签的比例，其值越大，漏检率越低。设P表示数据中真阳样例的数量，TP表示正确预测为正例的数量，FN表示错误预测为反例的数量，则定义为
  $$\mathrm{Sensitivity}=\mathrm{TPR}=\mathrm{Recall}=\frac{\mathrm{TP}}{\mathrm{P}}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}=1-\mathrm{FNR}$$

• 特异度(Specificity)

  也称真阴性率(True Negative Rate)和选择性(Selectivity)，表示预测为正的背景标签占所有真实背景标签的比例，其值越高则误诊率越低。设N表示数据中真阴样例的数量，TN表示正确预测为负例的数量，FP表示错误预测为正例的数量，则定义为
  $$\mathrm{Specificity}=\mathrm{Selectivity}=\mathrm{TNR}=\frac{\mathrm{TN}}{\mathrm{N}}=\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}}=1-\mathrm{FPR}$$

• 阳性预测值(Positive Predictive Value，PPV)

  也称精确度(Precision)，指在所有样本的预测结果中，真阳性占所有阳性样本的比例，其值越大越好。设TP表示正确预测为正例的数量，FP表示错误预测为正例的数量，则定义为
  $$\mathrm{Precision}=\mathrm{PPV}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}=1-\mathrm{FDR}$$

2.MedPy安装

medpy安装较为简单，此处以Ubuntu 18.04.5 LTS系统的root用户为例，其他情况详见参考文献安装即可。

为了启用graph-cut包，我们需要安装下列软件包

sudo apt-get install libboost-python-dev build-essential

然后使用阿里云镜像源高速安装medpy

sudo pip install medpy -i http://mirrors.aliyun.com/pypi/simple/ --trusted-host mirrors.aliyun.com

3.MedPy常用函数

3.1 medpy.io.load(image)

加载图像并返回包含图像像素内容以及头部对象的 ndarray

import os
from medpy.io import load,save
# 文件夹路径和文件名
dirname="/dataset/RSNA_ASNR_MICCAI_BraTS2021_TrainingData_16July2021/BraTS2021_00000/"
basename="BraTS2021_00000_seg.nii.gz"
full_path=os.path.join(dirname,basename)
# 加载脑肿瘤标记图像返回图像数据数组和头部信息
image_data, image_header = load(full_path)

print("图像数据类型为,图像数据形状为".format(type(image_data),image_data.shape))

# 获取一个切片数组
slice_0=image_data[:,:,77]
Python第三方库之openpyxl(3)
区域图
区域图类似于折线图，绘图线下面的区域会被填充，通过将分组设置为“standard”、“stacked”或“percentStacked”，可以获得不同的变体;“standard”是默认的。
2D区域图
 

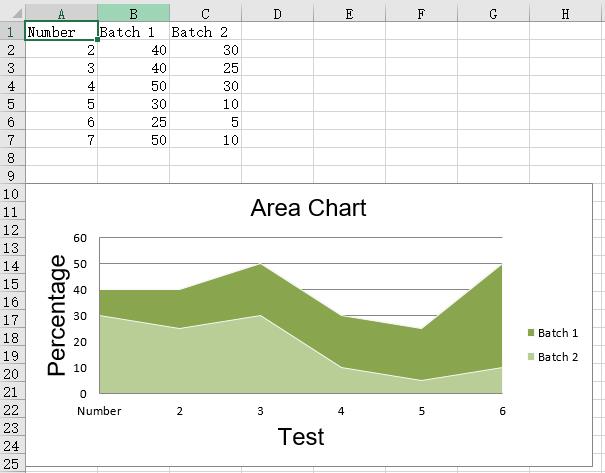
from openpyxl import Workbook
from openpyxl.chart import (
    AreaChart,
    Reference,
    Series,
)

wb = Workbook()
ws = wb.active

rows = [
    [\'Number\', \'Batch 1\', \'Batch 2\'],
    [2, 40, 30],
    [3, 40, 25],
    [4, 50, 30],
    [5, 30, 10],
    [6, 25, 5],
    [7, 50, 10],
]

for row in rows:
    ws.append(row)

chart = AreaChart()
chart.title = "Area Chart"
chart.style = 13
chart.x_axis.title = \'Test\'
chart.y_axis.title = \'Percentage\'

cats = Reference(ws, min_col=1, min_row=1, max_row=7)
data = Reference(ws, min_col=2, min_row=1, max_col=3, max_row=7)
chart.add_data(data, titles_from_data=True)
chart.set_categories(cats)

ws.add_chart(chart, "A10")

wb.save("area.xlsx")

运行结果：

 
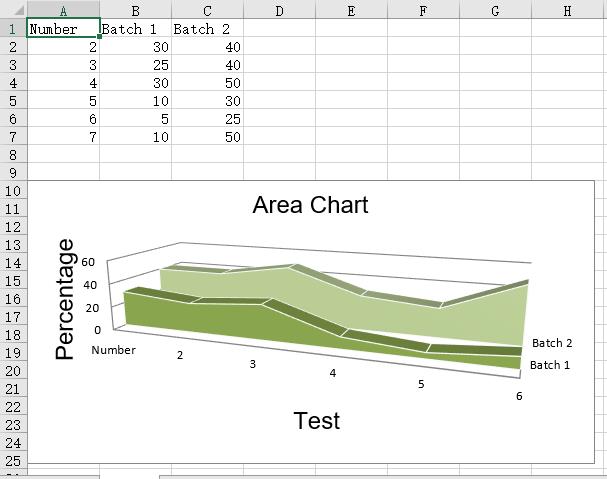
 3D区域图

from openpyxl import Workbook
from openpyxl.chart import (
    AreaChart3D,
    Reference,
    Series,
)

wb = Workbook()
ws = wb.active

rows = [
    [\'Number\', \'Batch 1\', \'Batch 2\'],
    [2, 30, 40],
    [3, 25, 40],
    [4 ,30, 50],
    [5 ,10, 30],
    [6,  5, 25],
    [7 ,10, 50],
]

for row in rows:
    ws.append(row)

chart = AreaChart3D()
chart.title = "Area Chart"
chart.style = 13
chart.x_axis.title = \'Test\'
chart.y_axis.title = \'Percentage\'
chart.legend = None

cats = Reference(ws, min_col=1, min_row=1, max_row=7)
data = Reference(ws, min_col=2, min_row=1, max_col=3, max_row=7)
chart.add_data(data, titles_from_data=True)
chart.set_categories(cats)

ws.add_chart(chart, "A10")

wb.save("area3D.xlsx")

运行结果