因子分析——python

Posted 2023-03-30 洋洋菜鸟

目录

一、起源

二、基本思想

三、算法用途

四、因子分析步骤

五、factor_analyzer库

四、实例详解

1.导入库

2.读取数据

3.充分性检测

3.1 Bartlett's球状检验

 3.2 KMO检验

4.选择因子个数

4.1 特征值和特征向量

4.2 可视化展示

4.3 可视化中显示中文不报错

5.因子旋转

5.1 建立因子分析模型

5.2 查看因子方差-get_communalities()

5.3 查看旋转后的特征值

 5.4 查看成分矩阵

 5.5 查看因子贡献率

 6.隐藏变量可视化

7.转成新变量

五·、参考资料

---

一、起源

        因子分析的起源是这样的：1904年英国的一个心理学家发现学生的英语、法语和古典语成绩非常有相关性，他认为这三门课程背后有一个共同的因素驱动，最后将这个因素定义为“语言能力”。

        基于这个想法，发现很多相关性很高的因素背后有共同的因子驱动，从而定义了因子分析，这便是因子分析的由来。

二、基本思想

        我们再通过一个更加实际的例子来理解因子分析的基本思想：

        现在假设一个同学的数学、物理、化学、生物都考了满分，那么我们可以认为这个学生的理性思维比较强，在这里理性思维就是我们所说的一个因子。在这个因子的作用下，偏理科的成绩才会那么高。

        到底什么是因子分析？就是假设现有全部自变量x的出现是因为某个潜在变量的作用，这个潜在的变量就是我们说的因子。在这个因子的作用下，x能够被观察到。

        因子分析就是将存在某些相关性的变量提炼为较少的几个因子，用这几个因子去表示原本的变量，也可以根据因子对变量进行分类。

        因子分子本质上也是降维的过程，和主成分分析（PCA）算法比较类似。

三、算法用途

        因子分析法和主成分分析法有很多类似之处。因子分析的主要目的是用来描述隐藏在一组测量到的变量中的一些更基本的，但又无法直接测量到的隐性变量。因子分析法也可以用来综合评价。

        其主要思路是利用研究指标的之间存在一定的相关性，从而推想是否存在某些潜在的共性因子，而这些不同的潜在的共性因子不同程度地共同影响着研究指标。因子分析可以在许多变量中找出隐藏的具有代表性的因子，将共同本质的变量归入一个因子，可以减少变量的数目。

四、因子分析步骤

应用因子分析法的主要步骤如下：

• 对所给的数据样本进行标准化处理

• 计算样本的相关矩阵R

• 求相关矩阵R的特征值、特征向量

• 根据系统要求的累积贡献度确定主因子的个数

• 计算因子载荷矩阵A

• 最终确定因子模型

五、factor_analyzer库

利用Python进行因子分析的核心库是：factor_analyzer

pip install factor_analyzer

这个库主要有两个主要的模块需要学习：

• factor_analyzer.analyze（重点）

• factor_analyzer.factor_analyzer

官网学习地址：factor_analyzer package — factor_analyzer 0.3.1 documentation

四、实例详解

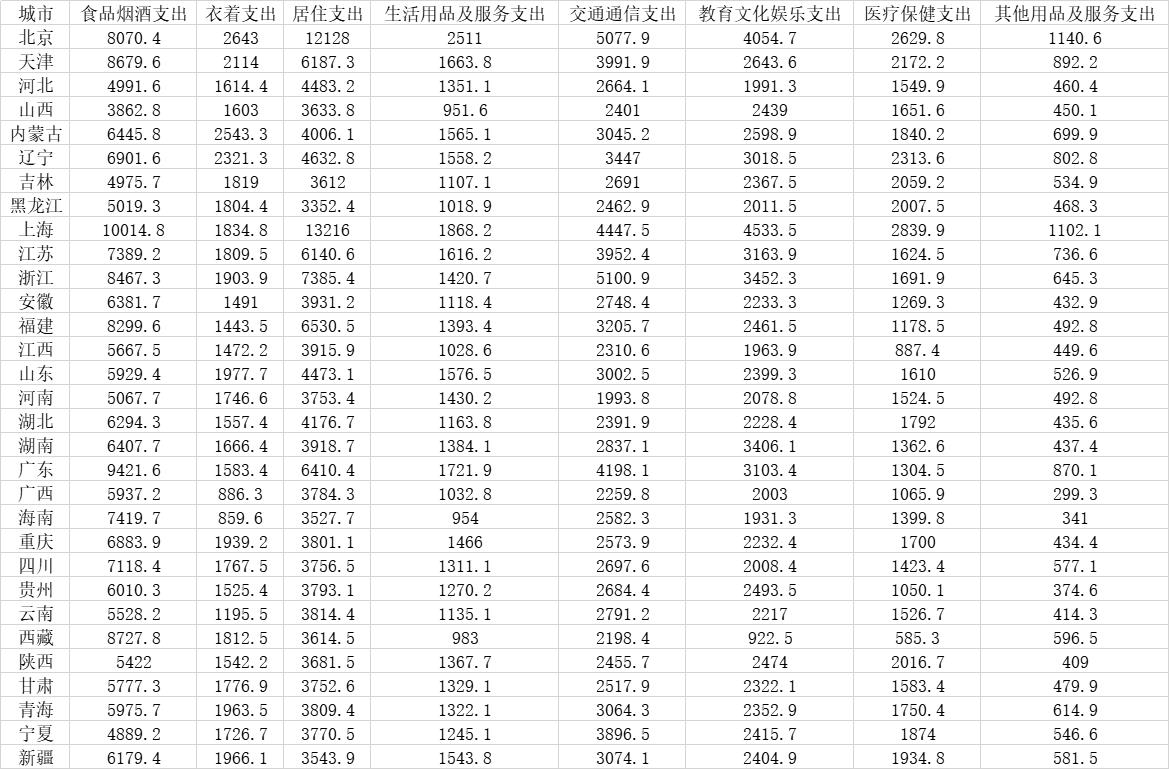
 数据来源于中国统计年鉴。

1.导入库

# 数据处理
import pandas as pd
import numpy as np

# 绘图
import seaborn as sns
import matplotlib.pyplot as plt
# 因子分析
from factor_analyzer import FactorAnalyzer

2.读取数据

df = pd.read_csv("D:\\桌面\\demo.csv",encoding='gbk')
df

输出：

 如果不想要城市那一列的话，可以在读取的时候就删除，也可以后面再删

比如，读取时删除

df = pd.read_csv("D:\\桌面\\demo.csv", index_col=0,encoding='gbk').reset_index(drop=True)
df

返回：

 然后我们查询一下，数据的缺失值情况：

df.isnull().sum()

返回：

 然后，我们可以针对的，对数据进行一次处理：

比如删除无效字段的那一列

#  去掉无效字段
df.drop(["变量名1","变量名2","变量名3"],axis=1,inplace=True)

或者，删除空值

# 去掉空值
df.dropna(inplace=True)

3.充分性检测

        在进行因子分析之前，需要先进行充分性检测，主要是检验相关特征阵中各个变量间的相关性，是否为单位矩阵，也就是检验各个变量是否各自独立。

3.1 Bartlett's球状检验

        检验总体变量的相关矩阵是否是单位阵（相关系数矩阵对角线的所有元素均为1,所有非对角线上的元素均为零）；即检验各个变量是否各自独立。

        如果不是单位矩阵，说明原变量之间存在相关性，可以进行因子分子；反之，原变量之间不存在相关性，数据不适合进行主成分分析

from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity

chi_square_value, p_value = calculate_bartlett_sphericity(df)
chi_square_value, p_value

返回：

 3.2 KMO检验

        检查变量间的相关性和偏相关性，取值在0-1之间；KOM统计量越接近1，变量间的相关性越强，偏相关性越弱，因子分析的效果越好。

通常取值从0.6开始进行因子分析

#KMO检验
from factor_analyzer.factor_analyzer import calculate_kmo
kmo_all,kmo_model=calculate_kmo(df)
kmo_model

返回：

 通过结果可以看到KMO大于0.6，也说明变量之间存在相关性，可以进行分析。

4.选择因子个数

方法：计算相关矩阵的特征值，进行降序排列

4.1 特征值和特征向量

faa = FactorAnalyzer(25,rotation=None)
faa.fit(df)

# 得到特征值ev、特征向量v
ev,v=faa.get_eigenvalues()
print(ev,v)

返回：

4.2 可视化展示

将特征值和因子个数的变化绘制成图形：

 # 同样的数据绘制散点图和折线图
plt.scatter(range(1, df.shape[1] + 1), ev)
plt.plot(range(1, df.shape[1] + 1), ev)

# 显示图的标题和xy轴的名字
# 最好使用英文，中文可能乱码
plt.title("Scree Plot")  
plt.xlabel("Factors")
plt.ylabel("Eigenvalue")

plt.grid()  # 显示网格
plt.show()  # 显示图形

返回：

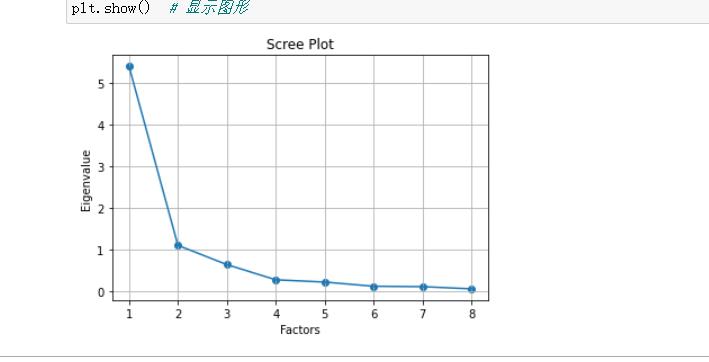
 从上面的图形中，我们明确地看到：选择2或3个因子就可以了

4.3 可视化中显示中文不报错

只需要在画图前，再导入一个库即可，见代码

import matplotlib as mpl

mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题

5.因子旋转

5.1 建立因子分析模型

在这里选择，最大方差化因子旋转

# 选择方式： varimax 方差最大化
# 选择固定因子为 2 个
faa_two = FactorAnalyzer(2,rotation='varimax')
faa_two.fit(df)

返回：

ratation参数的其他取值情况：

• varimax (orthogonal rotation)

• promax (oblique rotation)

• oblimin (oblique rotation)

• oblimax (orthogonal rotation)

• quartimin (oblique rotation)

• quartimax (orthogonal rotation)

• equamax (orthogonal rotation)

5.2 查看因子方差-get_communalities()

查看公因子方差

# 公因子方差
faa_two.get_communalities()

返回：

 查看每个变量的公因子方差数据

pd.DataFrame(faa_two.get_communalities(),index=df.columns)

返回：

5.3 查看旋转后的特征值

faa_two.get_eigenvalues()

返回：

pd.DataFrame(faa_two.get_eigenvalues())

返回：

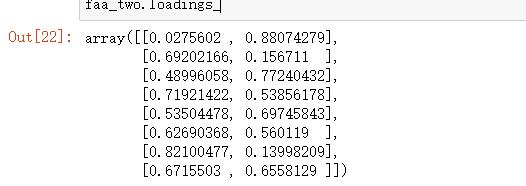
 5.4 查看成分矩阵

查看它们构成的成分矩阵：

# 变量个数*因子个数
faa_two.loadings_

返回：

 

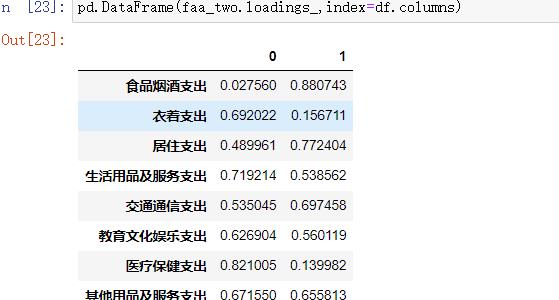
如果转成DataFrame格式，index就是我们的变量，columns就是指定的因子factor。转DataFrame格式后的数据：

pd.DataFrame(faa_two.loadings_,index=df.columns)

返回：

 5.5 查看因子贡献率

通过理论部分的解释，我们发现每个因子都对变量有一定的贡献，存在某个贡献度的值，在这里查看3个和贡献度相关的指标：

• 总方差贡献：variance (numpy array) – The factor variances

• 方差贡献率：proportional_variance (numpy array) – The proportional factor variances

• 累积方差贡献率：cumulative_variances (numpy array) – The cumulative factor variances

 我们来看一下总方差贡献吧

faa_two.get_factor_variance()

返回：

 

 6.隐藏变量可视化

为了更直观地观察每个隐藏变量和哪些特征的关系比较大，进行可视化展示，为了方便取上面相关系数的绝对值：

df1 = pd.DataFrame(np.abs(faa_two.loadings_),index=df.columns)
print(df1)

返回：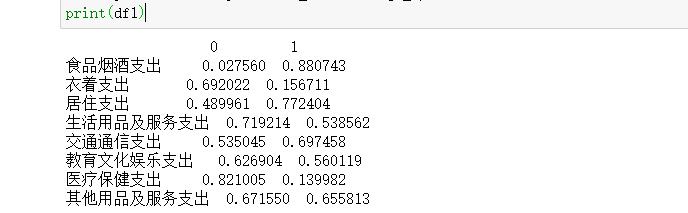

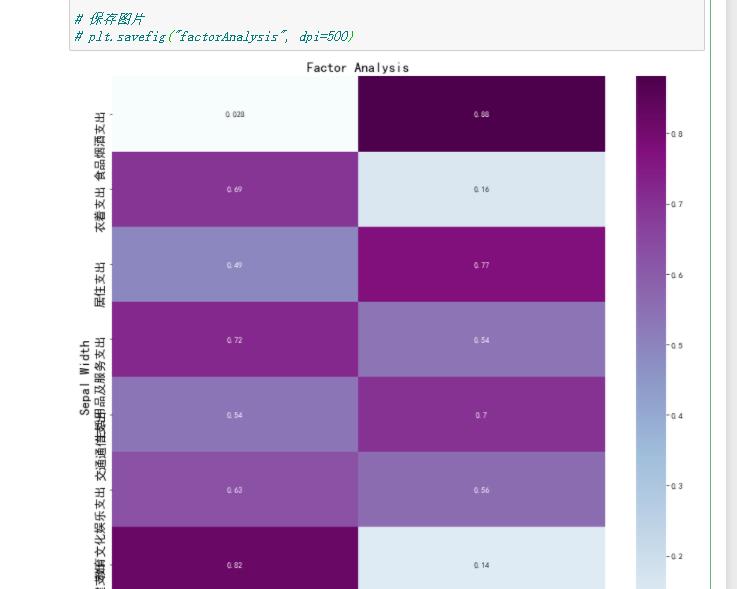
然后我们通过热力图将系数矩阵绘制出来：

# 绘图

plt.figure(figsize = (14,14))
ax = sns.heatmap(df1, annot=True, cmap="BuPu")

# 设置y轴字体大小
ax.yaxis.set_tick_params(labelsize=15)
plt.title("Factor Analysis", fontsize="xx-large")

# 设置y轴标签
plt.ylabel("Sepal Width", fontsize="xx-large")
# 显示图片
plt.show()

# 保存图片
# plt.savefig("factorAnalysis", dpi=500)

返回：

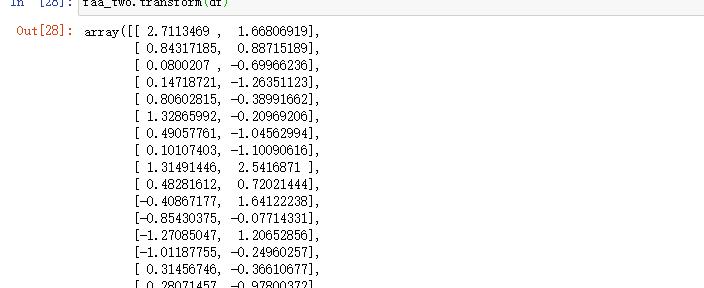
7.转成新变量

上面我们已经知道了2个因子比较合适，可以将原始数据转成2个新的特征，具体转换方式为：

faa_two.transform(df)

返回：

 转成DataFrame格式后数据展示效果更好：

df2 = pd.DataFrame(faa_two.transform(df))
print(df2)

返回：

五·、参考资料

1、Factor Analysis：Factor Analysis with Python — DataSklr

2、多因子分析：因子分析(factor analysis)例子–Python | 文艺数学君

3、factor_analyzer package的官网使用手册：factor_analyzer package — factor_analyzer 0.3.1 documentation

4、浅谈主成分分析和因子分析：浅谈主成分分析与因子分析 - 知乎

python 方差分析

方差分析Analysis of Variance，ANOVA是对变量之间关系的定性分析方法，其探究的是一个因子变量对反应变量的影响。

1.分类

类别	因子数量	举例	备注
单因素方差分析	1	失业率、股票收益率
多因素方差分析	>=2	施肥量和灌溉量对于粮食产量的影响	探究每个因子的影响，而不是因子整体的影响
析因方差分析	>=2	酗酒与年龄段	因子之间也存在着影响

补充：

2.实验的影响因素

1. 不可控的随机因素 指那些无法规避的影响，如相同的土地里，相同的种子，获取的产量却有所差异。
2. 可控的实验因素 通过分析不同来源的波动（不可控随机VS 可控因素）对总波动（反应变量的总体变化）的贡献大小，从而确定可控因素（因子）对反应变量影响力的大小。

3.三个重要概念

以单因素为例， 说明方差分析的假设检验过程。

3.1 离差平方和

假设现在因子变量共有 $M$个水平，每个水平下试验或观测对象有$N_j$个$(j=1,2,...,M)。$令$Y_ij$表示第$j$个水平组别下反应变量的均值，$μ_0$代表所有反应变量的均值。若因子水平对反应变量无影响，则不同因子水平下反应变量的均值是相同的，这就是方差分析之原假设∶ $$H_0: μ_1 = μ_2 = ... = μ_M = μ_0$$ 现在我们观测到不同因子水乎下的样本数据$y_ij(j=1,2,...M,i=1,2,...,N_j)$,这样第$j$组的样本均值: $$\\baryj = \\fracy1j+y_2j+...y_N_jjN_j=\\frac1N_j\\sum_i=1^N_jy_ij, j =1,2,...,M$$ 而全样本的平均值为:

$$\\bary = \\frac1N\\sum_j=1^MN_j \\baryj$$ 其中 $N = \\sumj=1^MN_j \\baryj$ 为全样本数量。方差分析实质就是检验$\\bary是否与\\baryj相异$，现在样本观测值$yij$ 与全样本均值$\\bary$之间的偏差可以分为两个部分： $$yij - \\bary = y_ij - \\baryj + \\baryj - \\bary$$ 其中，$yij - \\baryj$ 被称为组内偏差, $\\baryj - \\bary$ 称为组内偏差。将上式两边加总，就得到反映样本数据波动情况的指标——总离差平方 Total Sum of Squares TSS $$\\sumj=1^M\\sumi=1^N_j(yij-\\bary) ^2= \\sum_j=1^M\\sum_i=1^N_j(y_ij-\\baryj)^2 + \\sumj=1^M\\sum_i=1^N_j(\\baryj-\\bary) ^2=\\sumj=1^M\\sum_i=1^N_j(y_ij-\\baryj)^2 + \\sumj=1^MN_j(\\bary_j-\\bary) ^2$$

其中等号右边第一项为误差平方和 Error Sum of Square ESS;第二项为因子平方和 Factor Sum of Squares FSS

3.2自由度

自由度是指当以样本的统计量来估计总体的参数时，样本中能够独立或自由变动的数据的个数。比如，样本方差的计算公式为∶ $$S = \\frac1n-1\\sum_i=1^n(x_i-\\barx)^2$$ 其中分母$n-1$就是自由度。

总结起来，我们进行方差分析的对象共有 $N$ 个样本观测值，分布在 $M$ 个组中，第 $j$ 个组的样本量为 $N_j$。

• $TSS$ 是衡量的是$N$个样本的总波动水平，这里所有的$N$个样本并不独立，它们满足一个约束条件（均值为$\\bary$）: $$\\sum_j=1^M\\sum_i=1^N_j(y_ij-\\bary) = 0 $$ 故真正独立的变量只有N-1个，TSS的自由度为N-1。

• $FSS$ 衡量的是由于因子水平变化导致的反应变量取值的波动。但是，$M$ 个因子组别的均值并不独立，$\\baryj, j= 1,...,M$ 满足一个约束条件∶ $$\\sumj=1^MN_j(\\baryij-\\bary) = 0 $$ 因此也丢失一个自由度，$FSS$ 的自由度是 $M-1$，其平均数组间均方差为: $$MSF=\\fracFSSM-1=\\frac1M-1\\sumj=1^MN_j(\\bary_j-\\bary)^2$$

• $ESS$ 反应的是由于样本与其所处因子水平的组别均值的偏差而产生的波动，需要满足 $M$ 个约束条件 $$\\sum_i=1^N_j(y_ij-\\baryj) = 0 , j=1,...,N$$ 从而失去了 $M$ 个自由度，所以 $ESS$ 的自由度是 $N-M$ ，其平均数组内均方差为∶ $$MSE=\\frac1N-M\\sumj=1^M\\sum_i=1^N_j(y_ij-\\bary_j)^2$$

• $TSS$、$FSS$ 和 $ESS$ 的自由度满足如下关系: $$N-1=（M-1）+（N一M）$$

3.3显著性检验

假设反应变量$Y_ij$满足条件: 根据因子水平划分的任一 $j$ 组，$Y_ij（i=1，2…，N_j）$为一 组独立同分布变量，且服从正态分布，即$Y_ij～N（μ_j, \\sigma_0^2）$。基于这个假设，可证明出组间均方差和组内均方差的期望值满足下列公式∶ $$E(MSF)=\\sigma_0^2 + \\frac1M-1\\sum_j=1MN_j(\\mu_j-\\mu_0)^2$$ $$E(MSE)=\\sigma_0^2$$ 在原假设$H_0: \\mu_1=\\mu_1=...=\\mu_M=\\mu_0$, $E(MSF)=E(MSE)=\\sigma_0^2$,而且方差分析的统计量： $$\\varphi = \\fracMSFMSE=\\fracFSS/(M-1)ESS/(N-M)$$ 服从$F（M-1，N-M）$分布。

• $\\varphi$ 统计量越大，说明组间均方差$MSF$与组内均方差$MSE$差异很大，且$MSF>MSE$，故$MSF$ 成为样本总波动的主要贡献，因子影响十分显著;
• $φ$ 统计量很小时，说明组间随机方差$MSE$是主要的方差来源，因子影响不显著。

我们可以查阅$F分布$的临界值表，或者计算$p值$来判断该统计量是否显著。

4. 方差分析的python实现

导入statsmodel模块

import pandas as pd
import statsmodels.stats.anova as anova
from statsmodels.formula.api import ols

4.1 单因素方差分析

进行分析的数据如下：

• 代码实现

model = ols(收益率 ~ C(行业), data=year_return.dropna()).fit()
table1 = anova.anova_lm(model)
print(table1)

• 输出结果

>>>                df     sum_sq    mean_sq        F          PR(>F)
>>> C(行业)    2.0  0.073032  0.036516  1.193163  0.455962
>>> Residual  2.0  0.061209  0.030604      NaN        NaN

4.2多因素方差分析

多因素方差分析的实现也很简单，我们只需要在线性回归模型里加入要研究的因素即可。现在用其来探讨婚姻状况和受教育水平对个人收入的影响，数据如下（部分）：

• 代码实现

model = ols(earnings ~ C(married)+C(educatn), data=year_return.dropna()).fit()
table2 = anova.anova_lm(model)
print(table2)

• 输出结果

>>>                df      sum_sq        mean_sq        F         PR(>F)
>>> C(married)     6.0  1.956487e+10  3.260811e+09  15.551238   9.355695e-18
>>> C(educatn)    19.0  2.082990e+11  1.096311e+10  52.284500  9.947527e-180
>>> Residual      4829.0  1.012553e+12  2.096818e+08     NaN         NaN

4.3析因方差分析

析因方差分析与多元素方差分析差不多，仅是多了一个因子的乘项。比如在上面的例子中，可以添加 married与educatn的乘项，以检验这两者对收入的影响是否与另一个因子的水平有关。

>>>                           df        sum_sq  ...          F         PR(>F)
>>> C(married)                6.0  1.956487e+10  ...  15.476346   1.163717e-17
>>> C(educatn)               19.0  2.082990e+11  ...  52.032706  1.368466e-178
>>> C(married):C(educatn)   114.0  2.202005e+10  ...   0.916761   7.246151e-01
>>> Residual               4745.0  9.997547e+11  ...        NaN            NaN