日常Transformer要点记录及实现demo(PyTorch与Tensorflow)
Posted 囚生CY
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了日常Transformer要点记录及实现demo(PyTorch与Tensorflow)相关的知识,希望对你有一定的参考价值。
1 序言
近期抽空重整了一遍Transformer(论文下载)。
距离Transformer提出差不多有四年了,也算是一个老生常谈的话题,关于Transformer的讲解有相当多的线上资源可以参考,再不济详读一遍论文也能大致掌握,但是如果现在要求从零开始写出一个Transformer,可能这并不是很轻松的事情。笔者虽然之前也已经数次应用,但是主要还是基于Tensorflow和keras框架编写,然而现在Tensorflow有些问题,这将在本文的第三部分Tensorflow 实现与问题中详细说明。考虑到之后可能还是主要会在PyTorch的框架下进行开发,正好趁过渡期空闲可以花时间用PyTorch实现一个Transformer的小demo,一方面是熟悉PyTorch的开发,另一方面也是加深对Transformer的理解,毕竟将来大约是会经常需要使用,并且在其基础上进行改良的。
事实上很多事情都是如此,看起来容易,做起来就会发现有很多问题,本文在第一部分Transformer模型详解及注意点中将记录笔者在本次Transformer实现中做的一些值得注意的点;第二部分将展示PyTorch中Transformer模型的实现代码,以及如何使用该模型完成一个简单的seq2seq预测任务;第三部分同样会给出Tensorflow中Transformer模型的实现代码,以及目前Tensorflow的一些问题。
本文不再赘述Transformer的原理,这个已经有很多其他文章进行了详细说明,因此需要一些前置的了解知识,可以通过上面的论文下载 链接阅读原文。
目录
2 Transformer模型详解及注意点
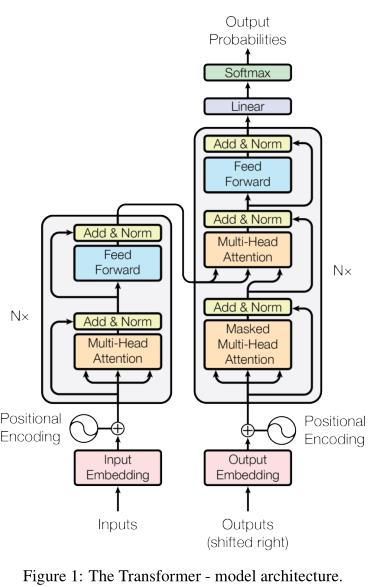
上图是Transformer的结构图解, 当中大致包含如下几个元素:
- Position Encoding: 位置编码;
- Position-wise Feed-Forward Networks: 即图中的Feed Forward模块, 这个其实是一个非常简单的模块, 简单实现就是一个只包含一个隐层的神经网络;
- Multihead Attention 与 Scaled Dot-Product Attention: 注意力机制;
- Encoder 与 Decoder: 编码器与解码器(核心部件);
- 关于上述部件在本文3.1节中的transformer.py代码中都有相应的类与其对应, 并且笔者已经做了非常详细的注释(英文), 以下主要就实现上的细节做说明, 可结合本文3.1节中的transformer.py代码一起理解;
-
Position-wise Feed-Forward Networks正如上述是一个非常简单的三层神经网络: F F N ( x ) = max ( 0 , x W 1 + b 1 ) W 2 + b 2 \\rm FFN(x) = \\max(0, xW_1 + b_1)W_2 + b_2 FFN(x)=max(0,xW1+b1)W2+b2隐层中使用的是ReLU激活函数(即 max ( 0 , x ) \\max(0,x) max(0,x)), 但是要确保的是该模块的输入与输出的维度是完全相同的;
-
关于Position Encoding的理解:
- Transformer中的Sinusoidal Position Encoding:
P
E
(
p
o
s
,
2
i
)
=
sin
(
p
o
s
1000
0
2
i
d
m
o
d
e
l
)
P
E
(
p
o
s
,
2
i
+
1
)
=
cos
(
p
o
s
1000
0
2
i
d
m
o
d
e
l
)
\\rm PE(\\rm pos,2i)=\\sin\\left(\\frac\\rm pos10000^\\frac2id_\\rm model\\right)\\\\\\rm PE(\\rm pos,2i+1)=\\cos\\left(\\frac\\rm pos10000^\\frac2id_\\rm model\\right)
PE(pos,2i)=sin(10000dmodel2ipos)PE(pos,2i+1)=cos(10000dmodel2ipos)
- p o s \\rm pos pos是位置的索引值, 即 0 , 1 , 2 , . . . , N − 1 0,1,2,...,N-1 0,1,2,...,N−1, N为序列长度;
- i i i是每个位置的Position Encoding的维度中的位置, 如将每个位置编码成64位的嵌入向量, 则 i i i取值范围就是 0 , 1 , 2 , . . . , 31 0,1,2,...,31 0,1,2,...,31, 2 i 2i 2i与 2 i + 1 2i+1 2i+1分别表示奇数位与偶数位;
- p o s + k \\rm pos+k pos+k位置的encoding可以通过 p o s \\rm pos pos位置的encoding线性表示得到: P E ( p o s + k , 2 i ) = sin ( w i ( p o s + k ) ) = sin ( w i p o s ) cos ( w i k ) + cos ( w i p o s ) sin ( w i k ) P E ( p o s + k , 2 i + 1 ) = cos ( w i ( p o s + k ) ) = cos ( w i p o s ) cos ( w i k ) − sin ( w i p o s ) sin ( w i k ) w i = 1 1000 0 2 i d m o d e l \\rm PE(\\rm pos+k,2i)=\\sin(w_i(\\rm pos+k))=\\sin(w_i\\rm pos)\\cos(w_ik)+\\cos(w_i\\rm pos)\\sin(w_ik)\\\\\\rm PE(\\rm pos+k,2i+1)=\\cos(w_i(\\rm pos+k))=\\cos(w_i\\rm pos)\\cos(w_ik)-\\sin(w_i\\rm pos)\\sin(w_ik)\\\\w_i=\\frac110000^\\frac2id_\\rm model PE(pos+k,2i)=sin(wi(pos+k))=sin(wipos)cos(wik)+cos(wipos)sin(wik)PE(pos+k,2i+1)=cos(wi(pos+k))=cos(wipos)cos(wik)−sin(wipos)sin(wik)wi=10000dmodel2i1化简得: P E ( p o s + k , 2 i ) = cos ( w i k ) P E ( p o s , 2 i ) + sin ( w i k ) P E ( p o s , 2 i + 1 ) P E ( p o s + k , 2 i + 1 ) = cos ( w i k ) P E ( p o s , 2 i + 1 ) − sin ( w i k ) P E ( p o s , 2 i ) \\rm PE(\\rm pos+k,2i)=\\cos(w_ik)\\rm PE(\\rm pos,2i)+\\sin(w_ik)\\rm PE(\\rm pos,2i+1)\\\\\\rm PE(\\rm pos+k,2i+1)=\\cos(w_ik)\\rm PE(\\rm pos,2i+1)-\\sin(w_ik)\\rm PE(\\rm pos,2i) PE(pos+k,2i)=cos(wik)PE(pos,2i)+sin(wik)PE(pos,2i+1)PE(pos+k,2i+1)=