二分查找+二分答案（Java）

Posted 2022-05-19 爱敲代码的三毛

文章目录

• 二分查找
• • 做法
  • • 下标问题
    • 边界问题
  • 图解
  • 代码实现
  • 复杂度分析
• 二分查找变形
• • • 1. 求满足条件的最小值(后缀)
    • 2. 求满足条件的最大值(前缀)
    • 3. 求最短子序列
    • 小结
    • 4. 大于x的平方数
    • 5.二分浮点数
• 二分答案
• • • 常规做法
    • 引入题目
    • 小结

---

二分查找

二分查找也叫折半查找，在一个有序（递增或者递减）的数列里寻找一个满足要求的数字

做法

如果我们要在一个有单调性的数组里查找某个数target，可以通过当前区间的最左边位置 left 和最右边位置right计算出中间位置 mid，再拿mid位置的元素和要找的元素 target 元素比较大小，来判断元素在在 mid 的左边还是右边，一次砍一半，重复此操作，找到可能的元素或者没有找到

下标问题

我们最直观的计算mid下标就是 通过 (left+right)/2,那么是否要考虑奇数和偶数的问题呢？

因为计算机在计算整数除法的时候是向下取整的 (1+3)/2 == (1+4)/2 的,无论是

边界问题

因为数组下标是从0开始的，为了方便计算mid下标，我们一般采取左闭右开区间，[left,right]

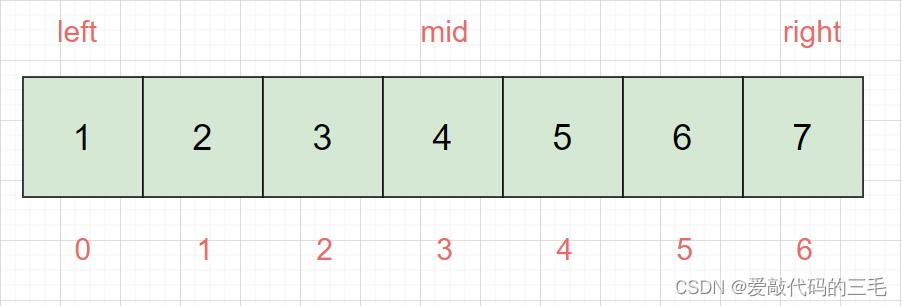
left 一般从0开始，不要管，

关键就是 right 的取值就关系到边界问题，也就是二分的结束条件

如果 right一般取的是数组最后一个下标，也就是数组长度 length-1

那么 二分的结束条件就是 left<=right，如果不取等于就会出现结果被忽略的情况

图解

代码实现

注意：((right-left)>>1)+left 等价于 (left+right)/2

递归

public static boolean dichotomy(int[] arr,int left,int right,int target) 
        // 边界判断
        if (left > right) 
            return false;
        
        int mid = ((right-left)>>1)+left;
        if (arr[mid] > target) 
            // 如果中间位置的数比要找的数还要大，说明要找的数组在左半部分
            return dichotomy(arr,left,mid-1,target);
         else if (arr[mid] < target) 
            // 如果中间位置的数比要找的数字还要小，说明要找的数在数组的右半部分
            return dichotomy(arr, mid+1, right, target);
         else 
            return true;
        
    

迭代

public static boolean dichotomy(int[] arr,int target) 
        int left = 0;
        int right = arr.length-1;
        int mid = 0;

        while (left <= right) 
            // 计算中间下标
            mid = ((right-left)>>1) + left;

            if (arr[mid] > target) 
                // 如果中间位置的数比要找的数还要大，说明要找的数组在左半部分
                right = mid-1;
             else if (arr[mid] < target) 
                // 如果中间位置的数比要找的数字还要小，说明要找的数在数组的右半部分
                left =  mid+1;
             else 
                return true;
            
        
        // 如果没有找到
        return false;
    

复杂度分析

因为二分查找都是每次将区间长度砍半，就是是每次区间都严格缩小一半，最差情况是区间长度变为零(找不到的情况)

n => $\frac{n}{2}=>\frac{n}{4}=>\frac{n}{8}...\overrightarrow{停止条件}\frac{n}{2^x},2^x\ge n$

根据停止条件$2^x\ge n得到x=logn$

算法运行次数为$x$,推出时间复杂度为 $O(x)=O(logn)$

二分查找变形

1. 求满足条件的最小值(后缀)

给定一个有单调性的数组 arr,问你大于等于$x$的最小值是多少(不存在输出No)?

思路：

因为这是一个单调序列，那么满足大于等于$x$条件的数一定是一个连续的区间，并且是从某一个位置一直往后(后缀)，然后要找的就是这个后缀的最左边的值，就是大于等于$x$的最小值。

假设当前的区间是$[l,r]$

1. 当 $x\le arr[mid]$,可行区间缩减成$[l,mid-1]$
2. 当 $x>arr[mid]$,则可行区间缩减成$[mid+1,r]$
3. 二分的条件是 $l<=r$

代码

public static void find(int[] arr, int x) 
        int left = 0;
        int right = arr.length-1;
        int mid = 0;

        while (left <= right) 
            mid = ((right-left)>>1)+left;
            if (arr[mid] >= x) 
                right = mid-1;
             else 
                left = mid+1;
            
        
        if (left  >= arr.length) 
            System.out.println("不存在大于等于"+x+"数");
         else 
            System.out.println(arr[left]);
        
    

假设序列是 $[1,2,4,7,9]$,我们要找大于等于 3的最小数字

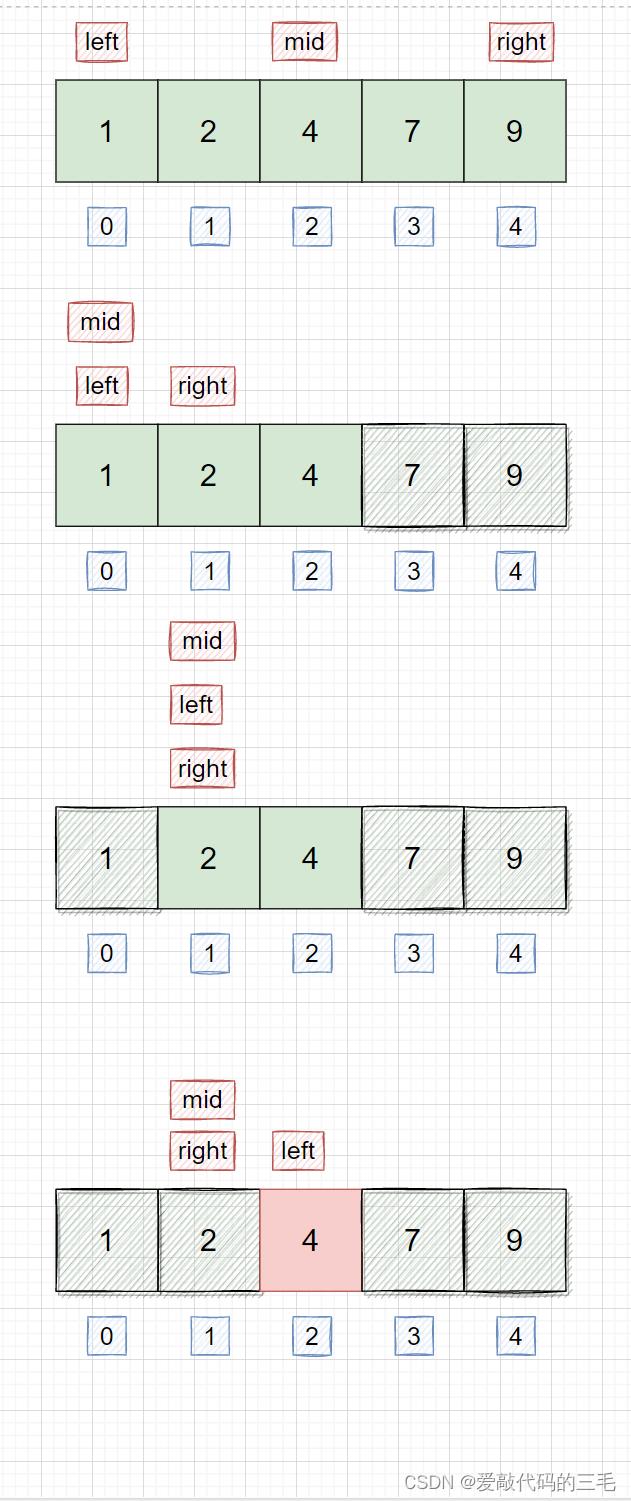
结论:最后的$l$一定停留在这个后缀的最左边的位置

2. 求满足条件的最大值(前缀)

给定一个有单调性的数组arr,问你小于等于$x$的最大值是多少？

思路：

和上一题类似，这也是一个单调序列，小于等于$$x$$的数也是一个连续的区间，这里是从某一个位置往前(前缀)的数字一定会小于等于x

假设区间是$[l,r]$

1. 如果$arr[mid]\le x,l=mid+1$
2. $如果arr[mid]>x,r=mid-1$
3. 二分的循环条件 $l\le r$

代码

public static void find(int[] arr,int x) 
        int left = 0;
        int right = arr.length-1;
        int mid = 0;
        while (left <= right) 
            mid = ((right-left)>>1)+left;
            if (arr[mid] <= x) 
                left = mid + 1;
             else 
                right = mid - 1;
            
        

        if (right < 0) 
            System.out.println("不存在小于等于"+x+"的数");
         else 
            System.out.println(arr[right]);
        
    

假设序列是 $[1,2,4,7,9],我们要找小于等于5的最大值$

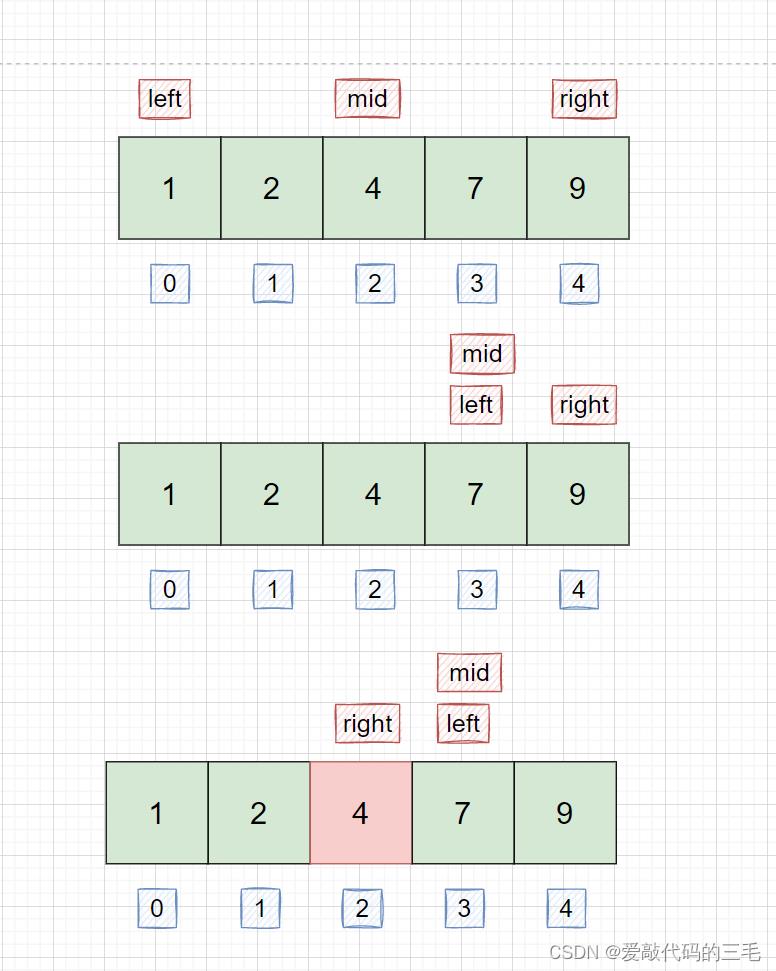
结论 ：最后 $r$ 一定停留在 前缀的最右边，也就是小于等于$x$最大值

3. 求最短子序列

给定一个正整数序列,让你取一个子段，使得其区间的和大于等于$x$,问你这个子段最短可能长度是多少。

例如:[1,2,4,7,9] ,给定 x = 13 时应该得到 2, x = 3 时应该得到1，x 大于 23时应该不存在

暴力代码

从 1、1+2、1+2+3、1+2…再到 2、2+4/2+4+7…枚举所有可能，当大于等于x时就break，因为前面的区间已经满足了条件，就是最短序列了没要继续往后

public static void shortestSubsequence(int[] arr, int x) 
    int min = Integer.MAX_VALUE;
    for (int i = 0; i < arr.length; i++) 
        int sum = 0;
        for (int j = i; j < arr.length; j++) 
            sum += arr[j];
            if (sum >= x) 
                min = Math.min(j-i+1,min);
                break;
            
        
    
    if (min != Integer.MAX_VALUE) 
        System.out.println(min);
     else 
        System.out.println("不存在");
    

小结

1.发现单调性： 固定左端点后，右端点越远，则区间的和越大。

2.做法：枚举左端点,二分找最近的右端点使得其大于等于$x$. 然后对所有左端点的答案取最小值。

3.预处理区间和：利用前缀和技巧。

4.复杂度：$O(nlogn)$

4. 大于x的平方数

给定一个数$x$,求解第一个大于$x$的平方数

二分思想，后缀模型

public static void maxFind(int x) 
        int left = 1;
        int right = x;
        int mid = 0;
        while (left <= right) 
            mid = ((right-left)>>1)+left;
            if (mid*mid > x) 
                right = mid-1;
             else 
                left = mid+1;
            
        
        System.out.println(left*left);
    

5.二分浮点数

给定一个数$x$,求解$\sqrt{x}$

二分与三分

Leetcode 4 Median of Two Sorted Arrays 二分查找（二分答案）

二分？三分！

二分与三分

算法1-6二分查找与二分答案 —— P2249 查找（来自洛谷 题单）