实时音频编解码之十三 Opus编码-SILK编码-噪声整形分析
Posted shichaog
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了实时音频编解码之十三 Opus编码-SILK编码-噪声整形分析相关的知识,希望对你有一定的参考价值。
本文谢绝任何形式转载,谢谢。
4.1.11 噪声整形分析
噪声整形的目的和原理性介绍见1.4.5小节,噪声整形是对量化误差能量谱的滤波技术,通常是去掉人耳敏感的频率,或者完全分离信号和噪声带;噪声整形量化利用了人耳的听觉特点,通常采用编码器最小化感知加权听觉误差以及解码器后滤波的方法抑制重构信号中相对于语音信号较高的量化噪声,Opus编码器通对输入和重构信号使用不同的权重滤波的方法将这两个部分都放在了编码侧,如下图所示,将这两部分放在编码侧并没有简单化解码侧,这使得编码侧可以使用任意简单或复杂感知模型同步或独立的进行噪声量化和频谱区域增强/抑制,Opus编码器使用扭曲的噪声整形滤波器,这是由于这些滤波器的频谱分辨率更适合人耳的听觉系统。
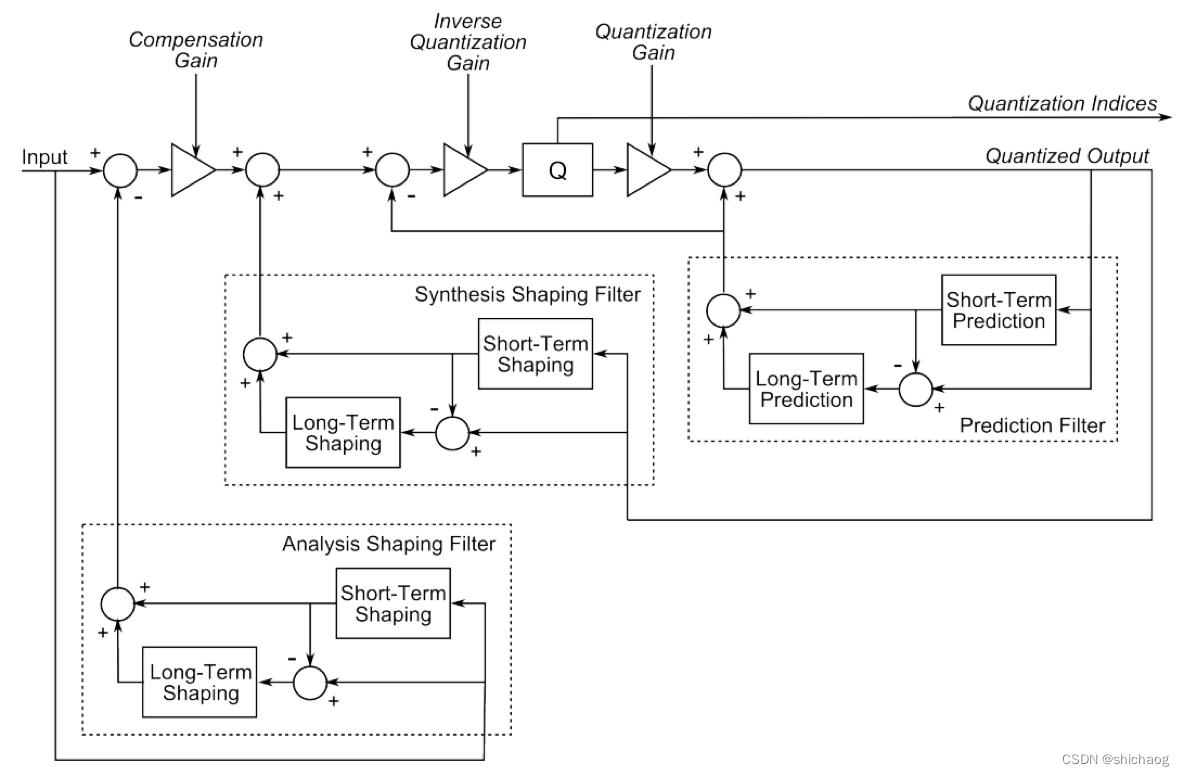
图: 预测噪声整形量化
Opus使用的噪声整形分析函数作用是计算噪声整形量化模块用于整形信号频谱时用到的增益和滤波器系数,噪声整形量化模块整形信号频谱的目的之一是将量化噪声谱和语音谱近似一致以便人的听觉系统不易察觉这类噪声,之二是抑制共振峰和谐波峰值之间的谱谷以便信号所含噪声更少,从这两方面改善编解码后的噪声。
对每个子帧会选择一个量化增益传给解码器,量化增益是量化噪声和量化比特率取舍的考量,量化增益确定了重构激励信号幅度的步长大小,此外在噪声整形分析时会提前和输入信号匹配的频谱倾斜以及和解码信号匹配的语音幅值。
输入信号使用如下滤波器滤波:
H
(
z
)
=
G
(
1
−
c
t
i
l
t
⋅
z
−
1
)
⋅
W
a
n
a
(
z
)
W
s
y
n
(
z
)
H(z) = G(1-c_tilt\\cdot z^-1)\\cdot \\fracW_ana(z)W_syn(z)
H(z)=G(1−ctilt⋅z−1)⋅Wsyn(z)Wana(z)
G是补偿增益,
c
t
i
l
t
c_tilt
ctilt是倾斜系数,对于语音分析滤波器如下:
W
a
n
a
(
z
)
=
(
1
−
∑
k
=
1
N
L
P
C
a
a
n
a
⋅
z
−
k
)
⋅
(
1
−
z
−
L
⋅
∑
k
=
−
2
2
b
a
n
a
(
k
)
⋅
z
−
k
)
W_ana(z)=(1-\\sum\\limits_k=1^N_LPCa_ana\\cdot z^-k)\\cdot(1-z^-L\\cdot \\sum \\limits_k=-2^2 b_ana(k)\\cdot z^-k)
Wana(z)=(1−k=1∑NLPCaana⋅z−k)⋅(1−z−L⋅k=−2∑2bana(k)⋅z−k)
w
s
y
n
w_syn
wsyn和此类似,
N
L
P
C
N_LPC
NLPC是噪声整形模块使用的LPC阶数,L是以点数为单位的pitch lag值,对于非语音,
(
1
−
z
−
L
⋅
∑
k
=
−
2
2
b
a
n
a
(
k
)
⋅
z
−
k
)
(1-z^-L\\cdot \\sum \\limits_k=-2^2 b_ana(k)\\cdot z^-k)
(1−z−L⋅k=−2∑2bana(k)⋅z−k)将被忽略以禁止谐波噪声整形。
短时噪声整形系数
a
a
n
a
(
k
)
a_ana(k)
aana(k)和
a
s
y
n
(
k
)
a_syn(k)
asyn(k)通过对输入信号
a
(
k
)
a(k)
a(k)的LPC系数使用不同的频带扩展计算得到,如:
a
a
n
a
(
k
)
=
a
(
k
)
⋅
g
a
n
a
k
a_ana(k)=a(k)\\cdot g_ana^k
aana(k)=a(k)⋅ganak
a
s
y
n
(
k
)
=
a
(
k
)
⋅
g
s
y
n
k
a_syn(k)=a(k)\\cdot g_syn^k
asyn(k)=a(k)⋅gsynk
频带扩展是得LPC多项式的根向原点偏移,因而平坦化了输入
a
(
k
)
a(k)
a(k)频谱。频带扩展因子计算方法如下:
g
a
n
a
=
0.95
−
0.01
⋅
C
g_ana=0.95-0.01\\cdot C
gana=0.95−0.01⋅C
g
s
y
n
=
0.95
+
0.01
⋅
C
g_syn=0.95 + 0.01 \\cdot C
gsyn=0.95+0.01⋅C
C
∈
[
0
,
1
]
C \\in [0,1]
C∈[0,1]是编码质量控制参数。相对于综合部分,分析部分使用更多的频带扩展会将谱谷弱化。对语音信号谐波噪声整形是如下三抽头滤波器。
b
a
n
a
=
F
a
n
a
⋅
[
0.25
,
0.5
,
0.25
]
b_ana=F_ana\\cdot[0.25, 0.5, 0.25]
bana=Fana⋅[0.25,0.5,0.25]
b
a
n
a
=
F
a
n
a
⋅
[
0.25
,
0.5
,
0.25
]
b_ana=F_ana\\cdot[0.25, 0.5, 0.25]
bana=Fana⋅[0.25,0.5,0.25]
F a n a ∈ [ 0 , 1 ] F_ana\\in [0,1] Fana∈[0,1]和 F s y n ∈ [ 0 , 1 ] F_syn\\in [0,1] Fsyn∈[0,1],其计算依赖于如下三个方面:
- 编码质量控制参数,这使得解码信号谐波性更强,这会使得低码率时编码简单;
- pitch相关性,周期性高的信号会给以更多的谐波整形以便一致谐波间的噪声;
- 1kHz以下信号的SNR,其通过加强谐波部分以滤除了带噪信号中的背景噪声。
和短时整形类似,通过使
F
a
n
a
<
F
s
y
n
F_ana < F_syn
Fana<Fsyn以增强pitch谐波性和抑制谐波之间的信号。
倾斜系数
C
t
i
l
t
C_tilt
Ctilt的计算如下:
C
t
i
l
t
=
0.25
+
0.2625
⋅
V
,
V
∈
[
0
,
1
]
C_tilt = 0.25 + 0.2625 \\cdot V, V\\in [0,1]
Ctilt=0.25+0.2625⋅