剑指offer(C++)-JZ84：二叉树中和为某一值的路径(数据结构-树)

Posted 2022-05-12 翟天保Steven

作者：翟天保Steven
版权声明：著作权归作者所有，商业转载请联系作者获得授权，非商业转载请注明出处

题目描述：

给定一个二叉树root和一个整数值 sum ，求该树有多少路径的的节点值之和等于 sum 。

1.该题路径定义不需要从根节点开始，也不需要在叶子节点结束，但是一定是从父亲节点往下到孩子节点

2.总节点数目为n

3.保证最后返回的路径个数在整形范围内(即路径个数小于231-1)

数据范围:

0<=n<=10000<=n<=1000

-10^9<=节点值<=10^9−109<=节点值<=109

假如二叉树root为1,2,3,4,5,4,3,#,#,-1，sum=6，那么总共如下所示，有3条路径符合要求

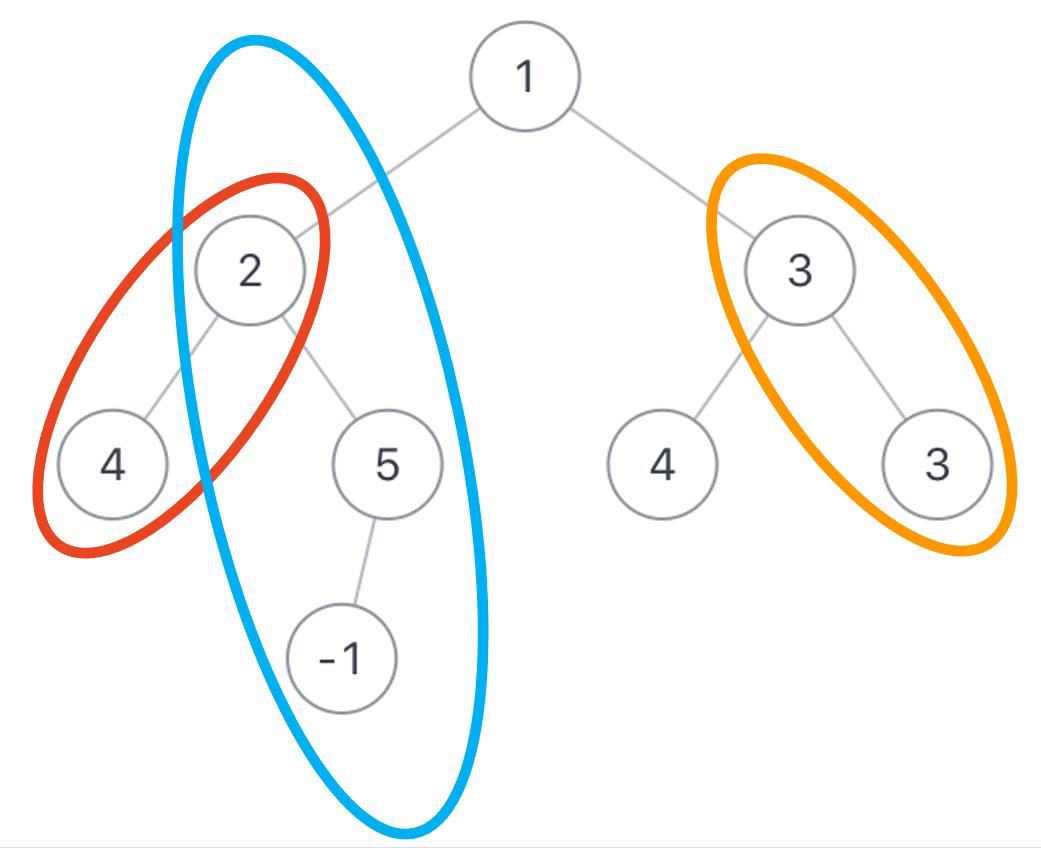
示例：

输入：

1,2,3,4,5,4,3,#,#,-1,6

返回值：

3

说明：

如图所示，有3条路径符合 

解题思路：

本题考察数据结构树的使用，可结合深度优先遍历dfs算法完成。

1. FindPath是寻找目标路径的函数，设计一个dfs函数执行深度优先遍历，寻找目标，再定义一个变量result，用来存储符合的路径条数。

2. dfs中当sum值与当前节点的值一致，说明当前的路径和是满足条件的；之后继续递归调用dfs，将节点的左右子树分别探索，注意此时的sum要变为sum-root->val，相当于前面已经走过路径，在动态累加。

3. dfs函数完整执行一遍，就是以root为起点的所有路径完成了一次遍历，但是题目中也可以找某一部分的路径，因此FindPath也要递归操作，将root的左右子树分别作为起点进行遍历，以此类推。最后返回的result就是所有满足条件的路径数。

测试代码：

/**
 * struct TreeNode 
 *	int val;
 *	struct TreeNode *left;
 *	struct TreeNode *right;
 *	TreeNode(int x) : val(x), left(nullptr), right(nullptr) 
 * ;
 */
class Solution 
public:
    // 结果数值
    int result=0;
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param root TreeNode类 
     * @param sum int整型 
     * @return int整型
     */
    int FindPath(TreeNode* root, int sum) 
        // 空节点返回
        if(!root)
            return result;
        // 根节点深度优先遍历
        dfs(root,sum);
        // 分别以左右子树为起点，进行遍历
        FindPath(root->left, sum);
        FindPath(root->right,sum);
        return result;
    
    
    // 深度优先遍历
    void dfs(TreeNode* root,int sum)
    
        // 空节点返回
        if(!root)
            return;
        // 找到目标，统计数加一
        if(sum==root->val)
            result++;
        // 左右子树继续探索，注意此时sum要减去当前节点的值
        dfs(root->left,sum-root->val);
        dfs(root->right,sum-root->val);
    
;