论文导读Continuity Scaling: A Rigorous Framework for Detecting andQuantifying Causality Accurately

Posted 2022-05-12 ViviranZ

【摘要】

在复杂的非线性动态系统中，基于数据的因果关系检测和量化对科学、工程和其他领域都是至关重要的。受近年来广泛使用的方法--基于交叉图的技术（the cross-map-based techniques）的启发，我们开发了一个通用框架，以推进对动态因果机制的全面理解，这与因果关系的自然解释是一致的。特别是，我们不是按照传统的方式来测量交叉图的平滑度，而是通过直接测量所研究的动态系统的连续性的缩放规律来定义因果关系。在一般复杂的动力系统中，未发现的缩放规律能够准确、可靠和有效地检测因果关系并评估其强度，优于那些现有的代表性方法。基于连续性标度的框架被严格地建立起来，并使用来自模型复杂系统和现实世界的数据集加以证明。

【综述】

识别和确定因果关系是一个对科学和工程极为重要的问题，具有广泛的应用[1-3]。例如，准确检测因果关系是识别精准医学中疾病起源的关键[4]，对精神病学等领域也很重要[5]。传统上，关联概念常常被误解为因果关系[6, 7]，而事实上，因果分析比关联更进一步，即不使用静态条件，而是在变化条件下诱发因果关系[8]。格兰杰因果关系原则正式确立了一个范式框架[9-11]，以预测改进的方式量化因果关系，但是，由于其线性、多变量和统计回归的性质，各种衍生方法需要大量的数据[12]。基于熵的方法[13-20]也面临类似的困难。格兰杰因果关系的另一个问题是对基础动态变量的可分离性的基本要求，这在现实世界的系统中通常无法满足。为了克服这些困难，基于交叉映射的技术，即为动态系统量身定做的范式，已经被开发出来，并在过去十年中得到了广泛的关注[21-36]。

交叉图起源于非线性时间序列分析[37-42]。对这种图的简单理解如下。考虑两个子系统。在X的重建相位空间中，如果对于任何一个时间的状态向量，可以找到一组相邻的向量，那么交叉映射的向量集，也就是X的同等时间的伙伴，可以在Y中找到。对于Y单向引起X的情况，重建空间的交叉映射可以写成Yt = Φ(X_t)（其中Xt和Yt是具有足够大维度的延迟坐标），而在数学上，其反映射不存在[34]。在实践中，利用对toy models中真实因果关系的先验知识或/和对Φ（在拓扑因果关系框架中用其大于1的雅各布奇异值表示[24]）的扩展特性的假设，科学家开发了许多基于交叉图的因果关系检测的实际有用技术。例如， the “activity” method，最初是为了测量交叉图的逆的连续性，将交叉图的向量与X中的状态向量的分歧与独立选择的相邻向量与同一状态向量的分歧进行比较[22, 23] 。拓扑因果关系测量交叉映射向量与Y中状态向量的发散率[24]，收敛交叉映射（CCM），增加时间序列的长度，将真实状态向量Y与交叉映射向量的平均值进行比较，作为Y的估计[21, 25-36]。然后，为了确定从Y到X的因果关系，对分歧的变化或估计的准确性进行统计评估。上述评价[21, 24, 26-36]可以在概念和定性的层面上理解，并在许多示范中表现良好。

在这项工作中，为了全面了解因果机制并受到基于交叉映射的技术的启发，我们开发了一个数学上严格的框架来检测非线性动力系统中的因果关系，将目光转向从交叉映射研究原始系统，这在逻辑上也与因果关系作为功能依赖的自然解释一致 [2, 8]。基于交叉地图的方法中使用的技能在我们的框架中被吸收，而我们直接研究原始动力系统或重建系统而不是交叉地图。我们框架的基础是由所研究系统的连续性引起的 ε 与 δ 变化关系的标度律，以下称为“连续性标度”。除了提供理论外，我们还使用合成数据和真实数据证明了我们的连续性缩放框架是准确的、计算效率高、适用范围广，与现有方法相比具有优势

  交叉映射（Convergent cross-mapping CCM)

https://zhuanlan.zhihu.com/p/36736341

重建相位空间

时间序列模型之相空间重构模型 - 知乎

连续性扩展框架

Case1

估计δt y的严格数学步骤在补充资料（SI）的第二部分给出。我们强调，这里研究的是xt+1和yt之间的对应关系，与基于交叉图的方法不同，自然产生一步的时间差。这种考虑产生了一个关键条件[DD]，只有在考虑原始迭代/流程时才需要，其详细描述和普遍性在SI中得到证明。我们揭示了hδt yi t∈ℕ和ln εx之间的线性缩放规律，如图1的下部面板所示，其斜率syx是ε和δ之间对应关系的指标，因此是因果关系yx。这里，h-it∈ℕ表示随时间变化的平均值。特别是，较大的斜率值意味着由地图函数fðxt, ytÞ所代表的从y到x的方向上有较强的因果关系（图1（a）），而接近零的斜率表示这个方向上的空因果关系（图1（b））。同样，在反方向，即xy方向的可能因果关系，由函数gð xt, ytÞ表示，可以用类似的方法评估。而当fðx, yÞ = f0ðxÞ独立于y的单向情况在案例二中被统一考虑。我们将考虑的情况总结如下，在SI的第二节中提供了关于比例法的通用存在的论证。

 Case2

 从v到u的因果关系是否意味着从y到x的因果关系？答案是肯定的。如果原始映射函数f独立于y：f(x, y) = f_0(x)，就不存在从y到x的因果关系。在这种情况下，嵌入E_u(x, y)变得独立于y，退化为E_u(x, y) = E_u0(x)的形式，只存在从M到L_u0 = E_u0(M)的微分同胚。因此，方程(4)变成u_t+1 =f^~_0(u_t)和v_t+1 =g^~(u_t, v_t)，其中f^~_0(u) = E_u0 ∘ f ∘ E^-1_u0(u)，由此产生的映射~f0与v无关。这种独立性可以通过计算与<δ_t>_t∈ℕ和ln ε_u之间的比例关系相关的斜率s_v→u来验证，其中零斜率表示从v到u的空因果关系，也就是从y到x的空因果关系。与之相对，有限的斜率定量表示变量之间的因果关系。因此，在重建的状态变量(u_t, v_t)_t∈ℕ之间检测到的任何类型的因果关系（单向或双向）都意味着在原始系统的内部但无法访问的变量x和y之间有相同类型的因果关系。

Case3

 内部变量的结构是完全未知的。给出观察函数u~, ~v: 我们首先重建状态空间：u~_t = （u~_t, u~_t+τ,⋯,u~_t+(d-1)τ) ^T；~v_t = (~v_t, ~v_t+τ,⋯,~v——t+（d-1)) ^T。为了检测和量化从~v到u~（或反之）的因果关系，我们用修改后的指数I^t_u~(ε_u~), δ^t_~v(ε_u~)和s_~v→u~进行连续性比例分析。与案例二不同的是，在这里，由于缺乏对内部变量和观测变量之间对应结构的了解，后者的因果关系并不肯定意味着前者也是如此。

Case4

连续时间动力系统拥有足够平滑的流S_t；t∈ℝ，在紧凑流形H上dS_t(u_0)/dt=χ(S_t(u_0)，其中χ是矢量场。让û_t=ωn+νg_n∈ℤ和v_t=ωn+νg_n∈ℤ分别为平滑观测函数û,v：H⟶ℝ，û_t=û(S_t), v_t=̂v(S_t)，其中1/ω为采样率，ν为时移。定义Ξ ≜ S_ω:H ⟶H和Ŝn ≜ S_ωn+ν(u_0)，我们得到一个离散时间系统：Ŝ_n+1 = Ξ(Ŝ_n)，观察函数为û_n = û(Ŝ_n)和 ̂v_n = ̂v( Ŝ_n）。将该案例还原为案例三，并使我们的连续性比例分析适用于揭示和量化û_t=ωn+νg_n∈ℤ和v_t=ωn+νg_n∈ℤ之间的因果关系。如果û和̂v的域对某些特定的子空间有自己的限制，例如û。Hu⟶ℝ和 ̂v: Hv⟶ℝ，H = Hu ⊕ Hv，情况就进一步简化为情况二，所以检测到的观察变量之间的因果关系意味着属于它们各自子空间的内部变量之间的因果关系。 

从复杂的动态模型到现实世界的网络 

为了证明我们的连续缩放框架的功效及其优越性能，我们用大量的合成和经验数据集进行了广泛的数值测试，包括来自基因调控网络以及空气污染和住院的数据集。连续性标度框架的实际步骤以及重要性测试程序在《方法》中有所描述。我们在此介绍三个有代表性的例子，而把其他有意义的例子留给SI。

第一个例子是两个单向互动物种的生态模型：

 

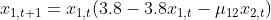
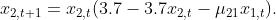
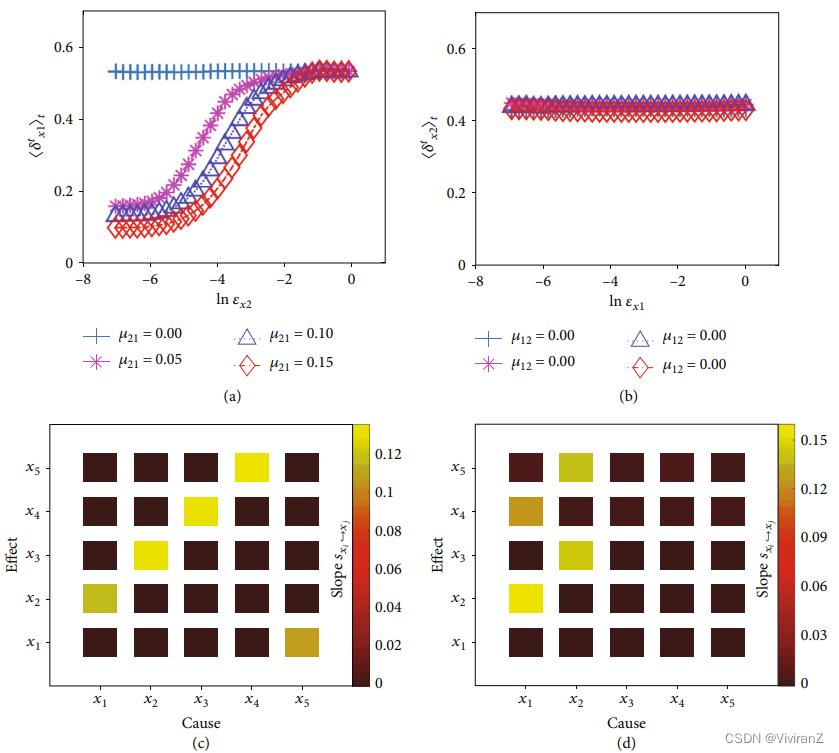
用不同的耦合参数值得到的时间序列fðx1,t, x2,tÞgt∈ℕ，我们的连续缩放框架产生了不同程度的单向因果关系的正确结果，如图3（a）和3（b）所示。在所有情况下，都存在一个合理的ln εx2的范围（既不会太小也不会太大），从中可以提取线性缩放的斜率sx1x2。估计斜率值的统计学意义以及由此产生的因果关系强度可以用标准的P值检验来评估[46]（方法和SI）。还测试了一个具有双向耦合的生态模型（见SI的第三部分）。图3(c)和3(d)分别显示了五个相互作用的物种在环状结构和树状结构上的生态网络的结果，其中彩色编码的斜率值准确反映了两种情况下的相互作用模式 

 p值检验 - 知乎

第二个例子是耦合的Lorenz系统：

，

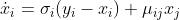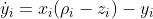
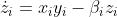
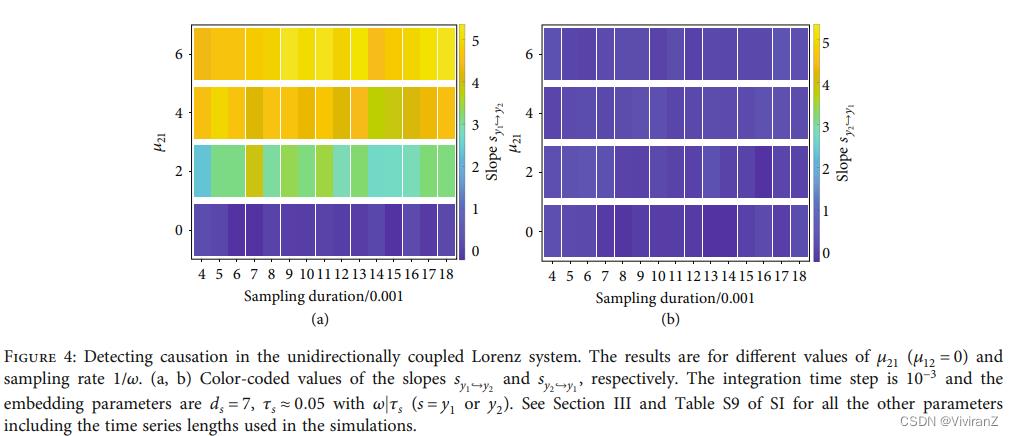
其中 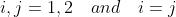。我们使用时间序列y_1,t, y_2,t_t=nω来检测不同的因果关系配置（见SI的第三部分）。图4显示了总体结果，其中用颜色编码的连续缩放的估计值显示了采样率1/ω和耦合强度的不同组合的斜率。即使采样率相对较低，我们的连续性标度框架也能成功地检测和量化因果关系的强度。此外，我们提出的指数可以准确地反映真实的因果关系强度（用耦合参数表示），这也被SI第三节和第四节的数字测试所证明。SI第三节提供了针对不同噪声扰动的稳健性测试，证明了我们框架的实用性。此外，与第一个例子类似，我们在SI中提出了几个关于具有非线性耦合的Lorenz系统和Rössler-Lorenz系统等的因果关系检测的例子，这进一步证明了我们框架的通用功效。

此外，我们还提出了对几个真实世界数据集的研究，

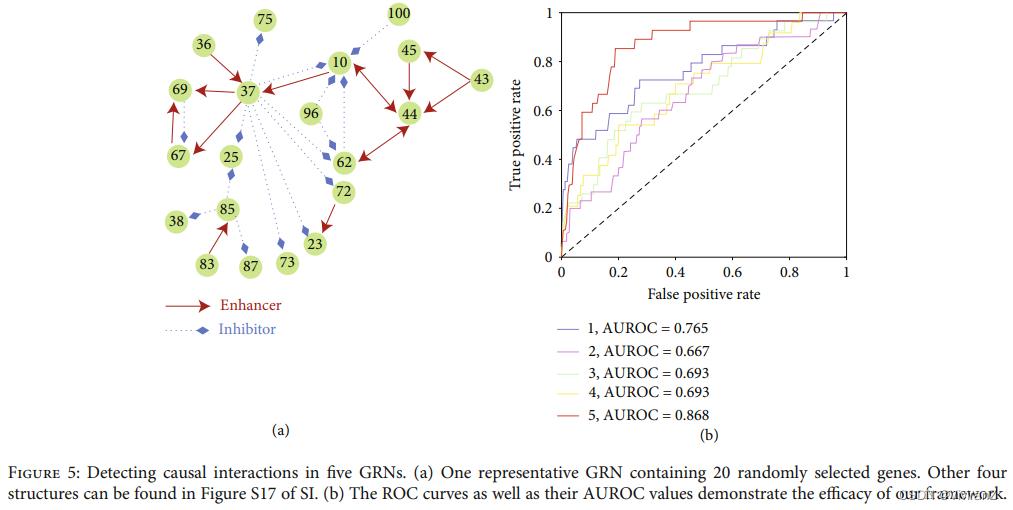
这为基础系统的进化机制带来了新的见解。我们研究了来自DREAM4 in silico Network Challenge[47, 48]的基因表达数据，其内在的基因调控网络（GRNs）是已知的验证（图5（a）和SI的图S17）。将我们的框架应用于这些数据，我们通过使用连续性缩放框架确定每对基因之间的因果关系。图5(b)显示了五个不同网络的相应ROC曲线以及它们的AUROC值，这表明在处理真实世界的数据时具有很高的检测精度。 

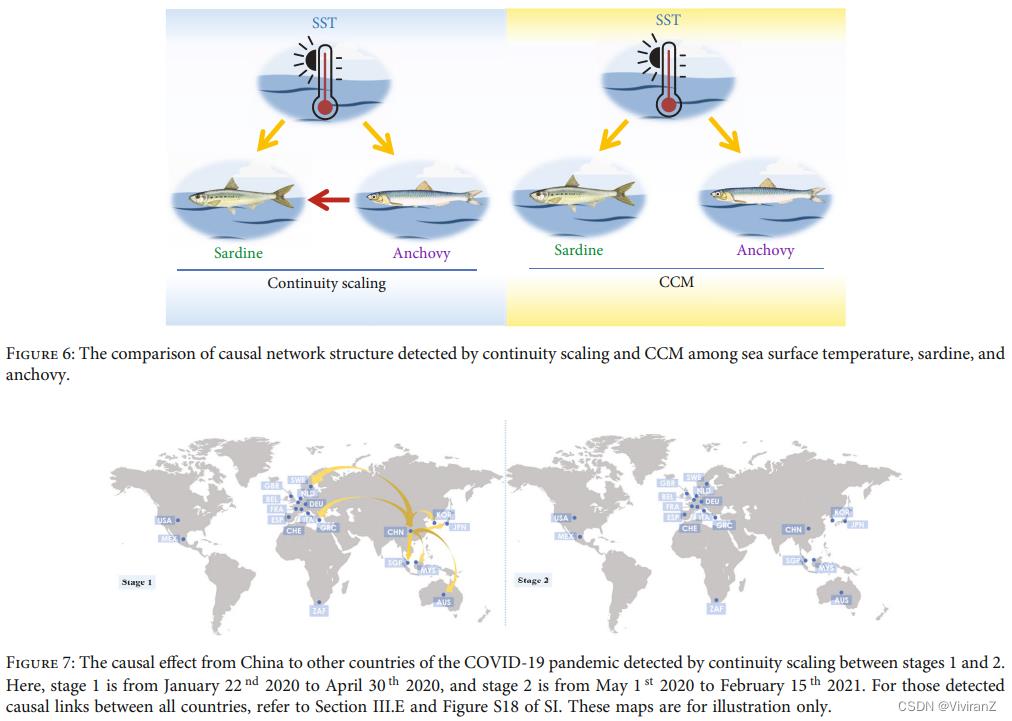
然后，我们在一个由太平洋沙丁鱼上岸量、北方鳀鱼上岸量和海表温度(SST)组成的海洋生态系统中检验了这种因果关系。我们揭示了新的发现, 支持[49]中所述的竞争关系假说, 这些假说无法通过CCM[25]检测出来. 如图 6 所示，虽然两种方法都验证了 SST 对两个物种的共同影响，但我们的连续缩放法还显示了 鳀鱼对沙丁鱼的明显影响，其反方向的影响则不明显。虽然竞争关系在生态系统中起着重要的作用, 但连续缩放法可以揭示出更重要的相互作用机制. 更多细节见SI的III.E节。

此外，我们研究了最近COVID-19大流行的传播机制。特别是，我们分析了两个阶段的代表性国家的COVID-19的每日新病例：第1天（2020年1月22日）到第100天（2020年4月30日）和第101天（2020年5月1日）到第391天（2021年2月15日）。我们的连续性缩放法被成对地应用于重构传播因果网络。如图7所示，中国在第一阶段对几个国家表现出明显的影响，这种影响在第二阶段消失了。然而，其他国家的情况与中国不同，中国的外部效应持续存在，如第三章E节和SI的图S18所示。我们的结果与中国持有严格的流行病控制策略和零星的国内感染相一致，这一点从官方的每日简报中可以看出，在检测正在进行的复杂系统的因果网络方面，连续性扩展具有潜力。此外，我们强调，第100天是一个合适的临界日，以区分大流行病的早期严重阶段和后期良好控制阶段（见SI的图S18（a）），而临界日的轻微变化不会使我们的结果无效。如SI图S18(b)所示，当临界日从第94天到第106天变化时，两个阶段检测到的因果关系都没有发生明显变化（小于5%），第二阶段受中国影响的国家数量仍然为零。更多细节见SI的III.E节.

其他现实世界的例子，包括香港的空气污染物和入院记录，也显示在SI的第三部分。

  

讨论和未来工作

综上所述，我们开发了一个新的框架，用于基于数据的复杂动态系统中因果关系的检测和量化。在广泛使用的基于交叉图的技术的基础上，我们的框架享有一个严格的基础，直接关注相关系统的连续性比例法，而不是只调查其交叉图的连续性。因此，我们的框架与因果关系的标准解释是一致的，甚至在现有的几种典型方法表现不佳甚至失败的情况下也能发挥作用（见SI第四节的比较结果）。此外，导致我们框架核心的数学推理，即连续性缩放，有助于解决与直接使用交叉图的技术相关的长期问题，即需要有关结果变量的信息来预测因果变量的动态行为，而文献[50]中的几项工作，直接研究交叉图的连续性或平滑性，很可能在因果方向上产生混淆的检测结果。
计算复杂度：该算法的计算复杂度为O(T^2N_ε)，相对小于CCM方法，其计算复杂度为O(T_2log T)。
限制和未来工作：尽管如此，目前提出的框架仍有一些改进的空间。首先，目前只设计了双变量检测算法，因此对多变量网络推理的推广需要进一步考虑，这与文献[51-53]中的工作类似。第二，目前的框架没有考虑到因果时间延迟，所以也可以进一步研究，类似于文献[33]中报告的工作。[33]. 另外，更先进的算法，如参考文献[54]中开发的算法，也可以整合到框架中。[54]中开发的算法，可以整合到这个框架中，以检测那些时间性的因果结构。当然，我们将在未来的工作中解决这些问题。
检测复杂动态系统中的因果关系不仅在科学和工程方面有广泛的应用，而且在现代社会的许多方面也有广泛的应用，需要准确、高效、严格的论证，因此是值得信赖的方法论。我们目前的工作提供了一个沿着这一壮举的载体，并确实解决了在使用这些有影响力的方法时产生的困惑

【Method】

 

Kennel等人[28]提出了一种确定最小充分嵌入维度m的方法。它被称为假近邻法。这个想法是非常直观的。假设一个给定的时间序列x_i_i\\in N的最小嵌入维度是m0。这意味着在一个m0维的延迟空间中，重建的吸引子是原始相空间中吸引子的一对一图像。特别是，拓扑学特性被保留下来。因此，一个给定的点的邻居被映射到延迟空间中的邻居。由于假定动力学的平稳性，点的邻域又被映射到邻域上。当然，邻域的形状和直径会根据李亚普诺夫指数而改变。但假设你现在嵌入到一个m<m0的m维空间。由于这种投射，拓扑结构不再被保留。点被投射到其他点的邻域，而这些点在更高的维度上是不属于这些邻域的。这些点被称为假邻居。如果现在应用动力学，这些假邻居通常不会被映射到邻域的图像中，而是被映射到其他地方，因此平均 "直径 "变得相当大。