Carsim Simulink自动驾驶仿真基于MPC的速度控制

Posted 2023-03-29 薯一个蜂蜜牛奶味的愿

本人也是刚开始探索，大家一起讨论一起进步！
项目介绍：
教程为北理工的无人驾驶车辆模型预测控制第2版，代码为开源代码。所用的仿真软件为Carsim2020.0和MatlabR2021a。使用MPC控制思想对车辆进行速度控制，并给出仿真结果。
效果如下：

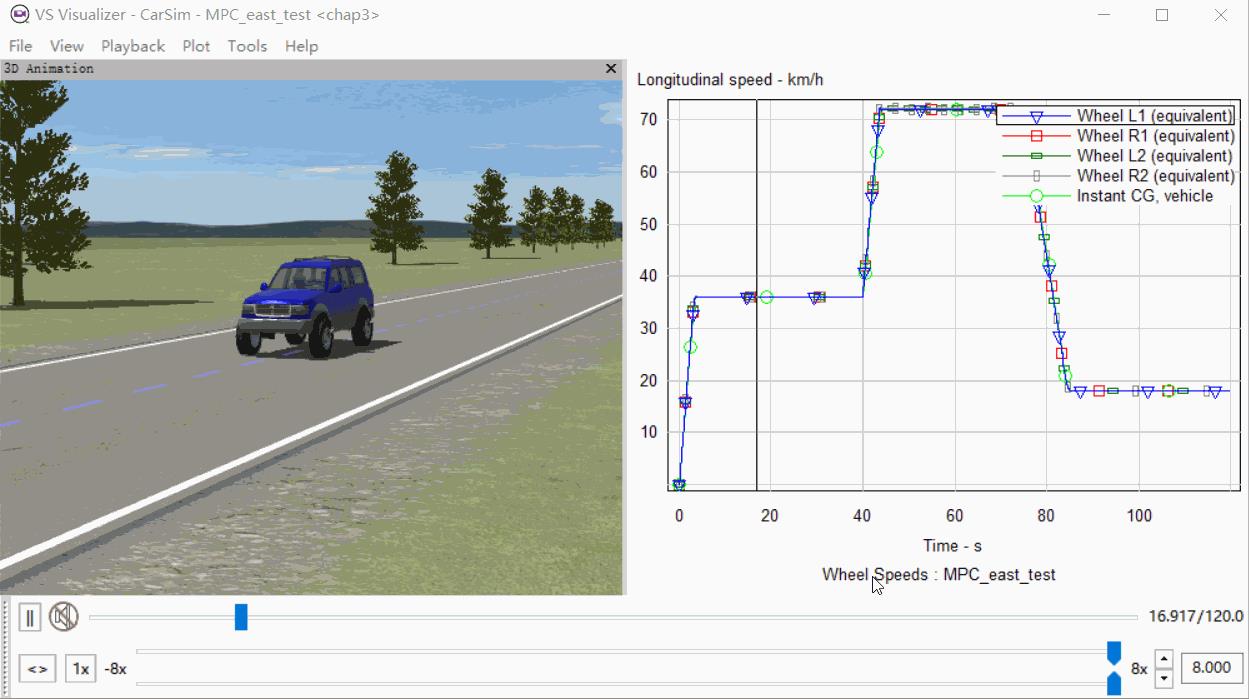
基于MPC的速度控制

• Carsim的基本配置
• • 车型的选择
  • 工况设置
• Carsim与Matlab的接口设置
• Matlab 框架搭建
• MPC速度控制理论
• • 问题描述
  • 速度跟踪MPC建模
  • MPC求解转化为二次型规划求解(把模型约束放入目标函数)
  • • 使用模型，对未来的状态和控制进行预测，并给出解析结果
    • 将预测的表达式带入目标函数，对其进行改写
    • 统一控制变量
    • 写成二次型问题
• 后处理
• 附录：Matlab全代码

Carsim的基本配置

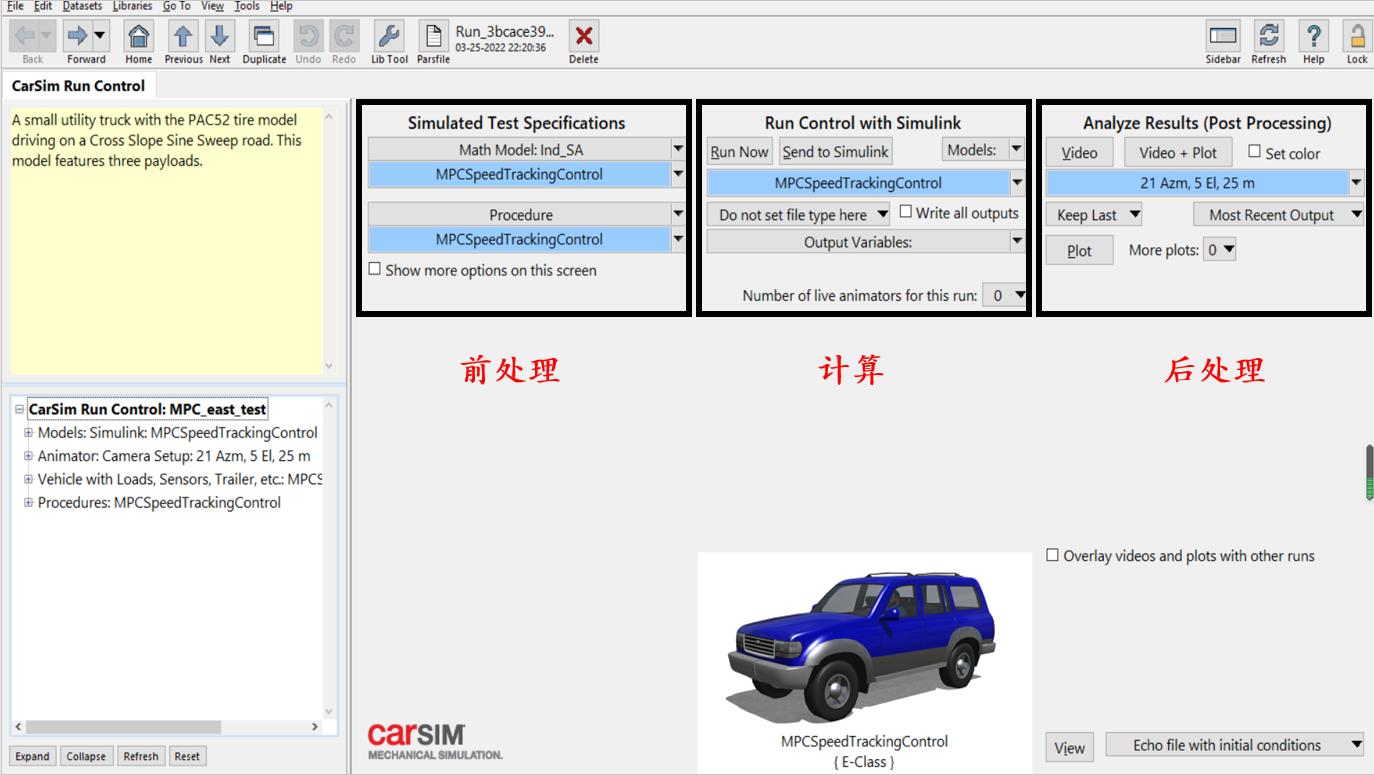
Carsim一共可以分为三大部分：

• 前处理：涉及对车型的选择和对工况的设置
• 计算：可以使用Carism直接计算，也可以外接其他计算软件，比如Matlab。
• 后处理：将运行的结果表现成动画和图像。
  具体分布如下：
  

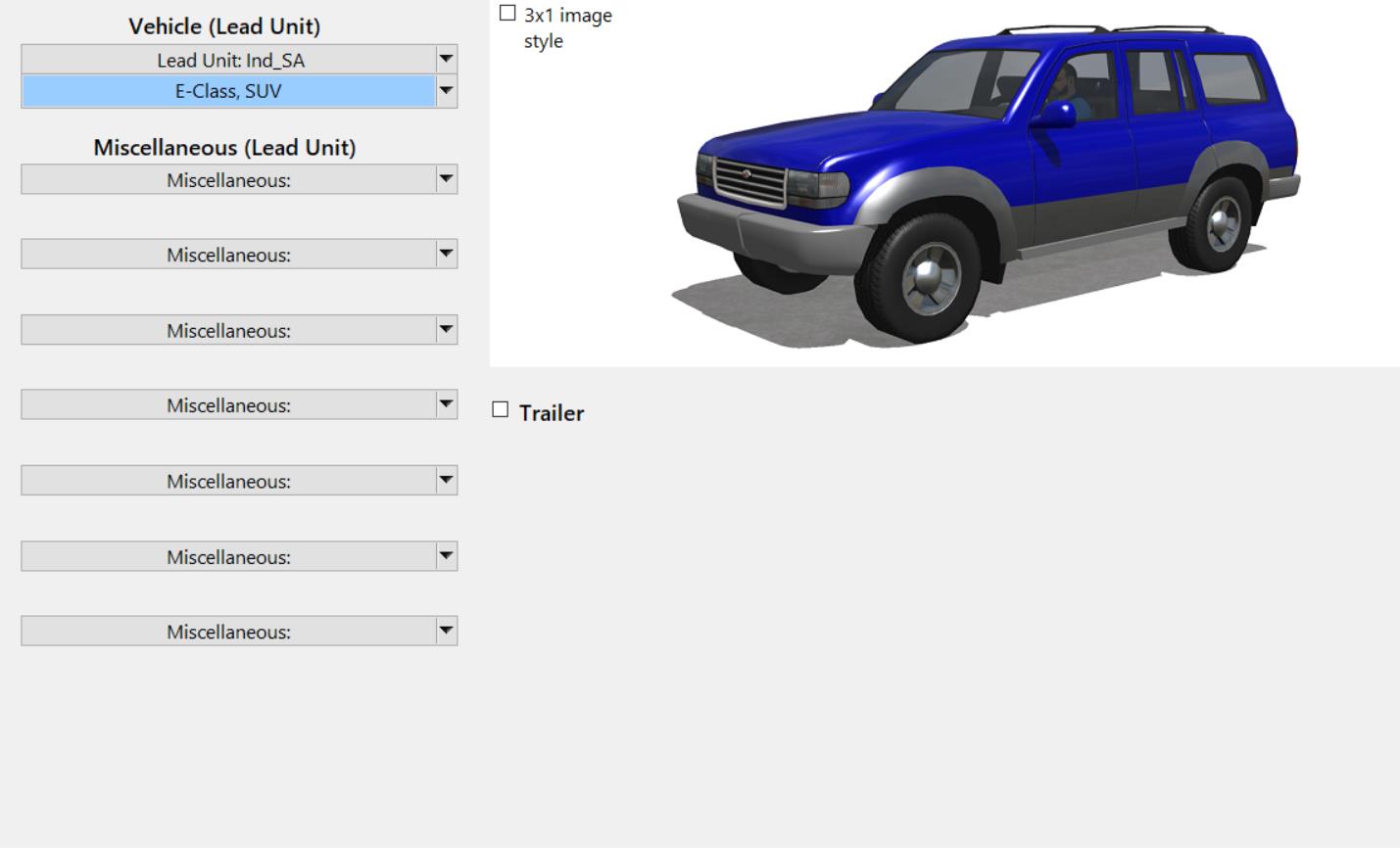
车型的选择

车型选择E-Class SUV，最好开一个新的Dataset。

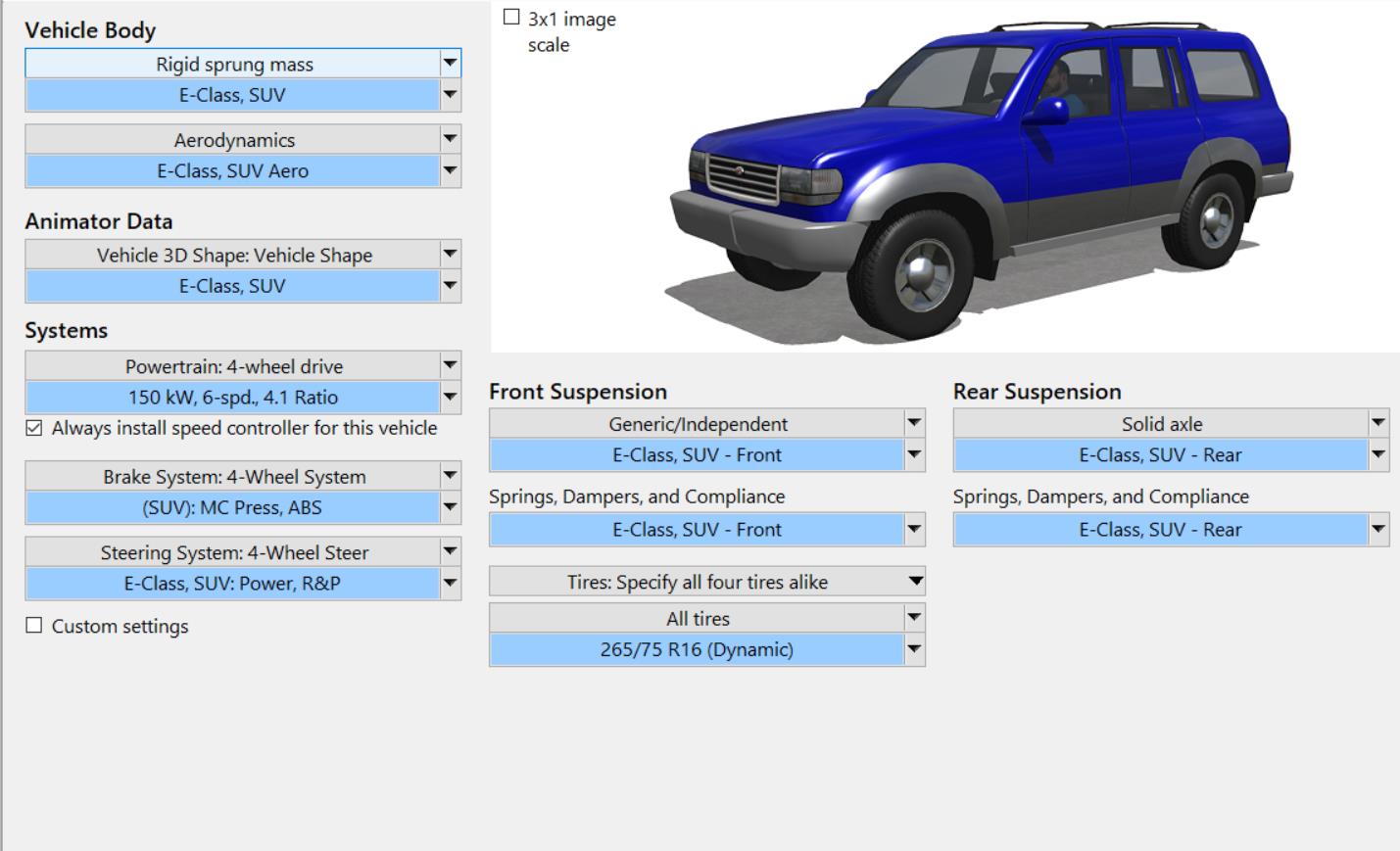
工况设置

新开一个Dataset。因为我们需要在MATLAB中控制汽车，不需要模型自身施加驱动力和制动力所以驱动控制和制动控制设置为无。挡位选择自动升档。本项目无横向控制，所以转向盘选择”Driver path follower“控制。道路设置长一点，仿真设置120s，具体参数设置如下：

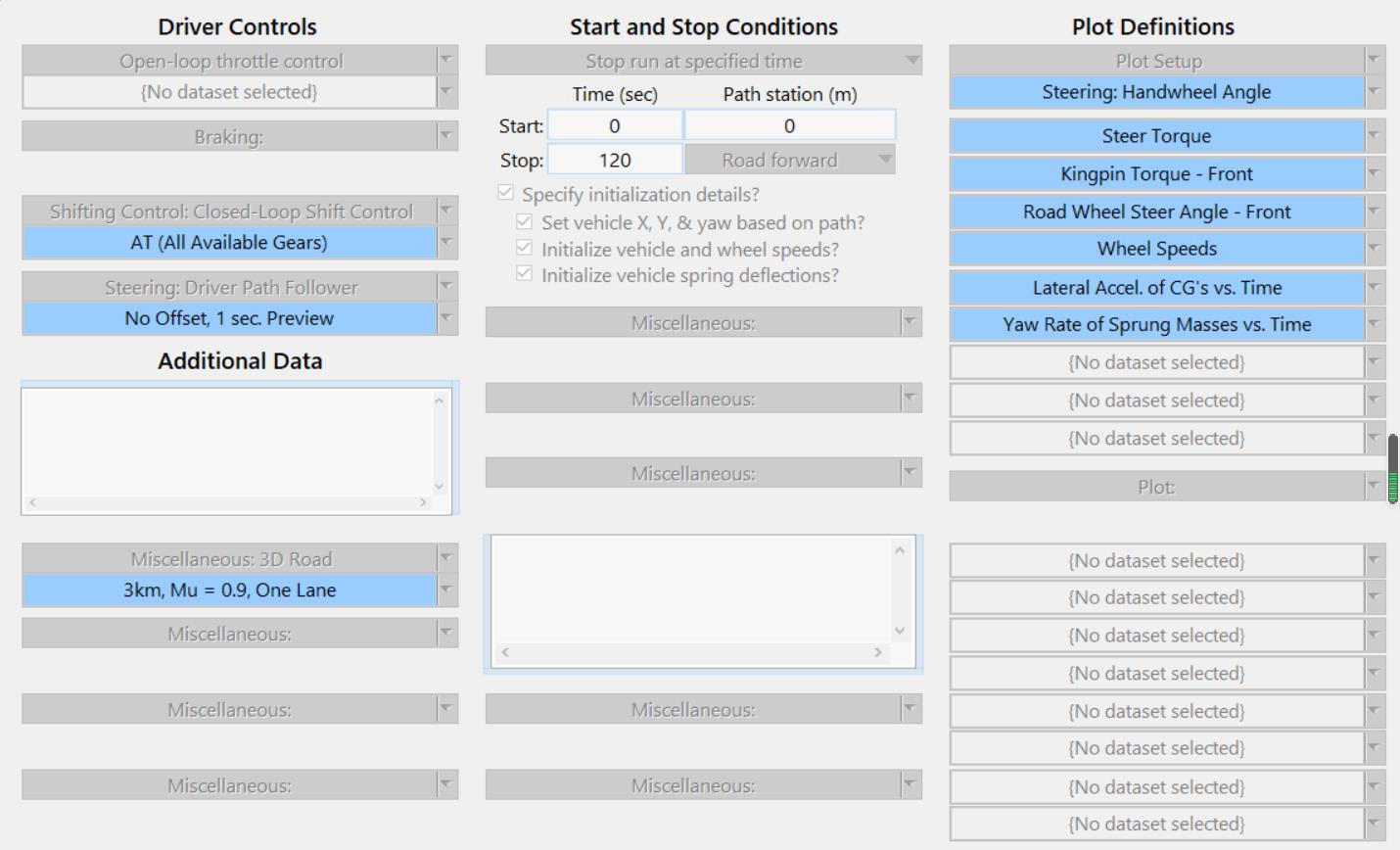
Carsim与Matlab的接口设置

在设置完前处理之后，准备使用MATLAB中的Simulink对其进行控制和计算。在计算那一栏的Model中选择Model:Simulink。之后建立一个新的Dataset。具体设置如下：

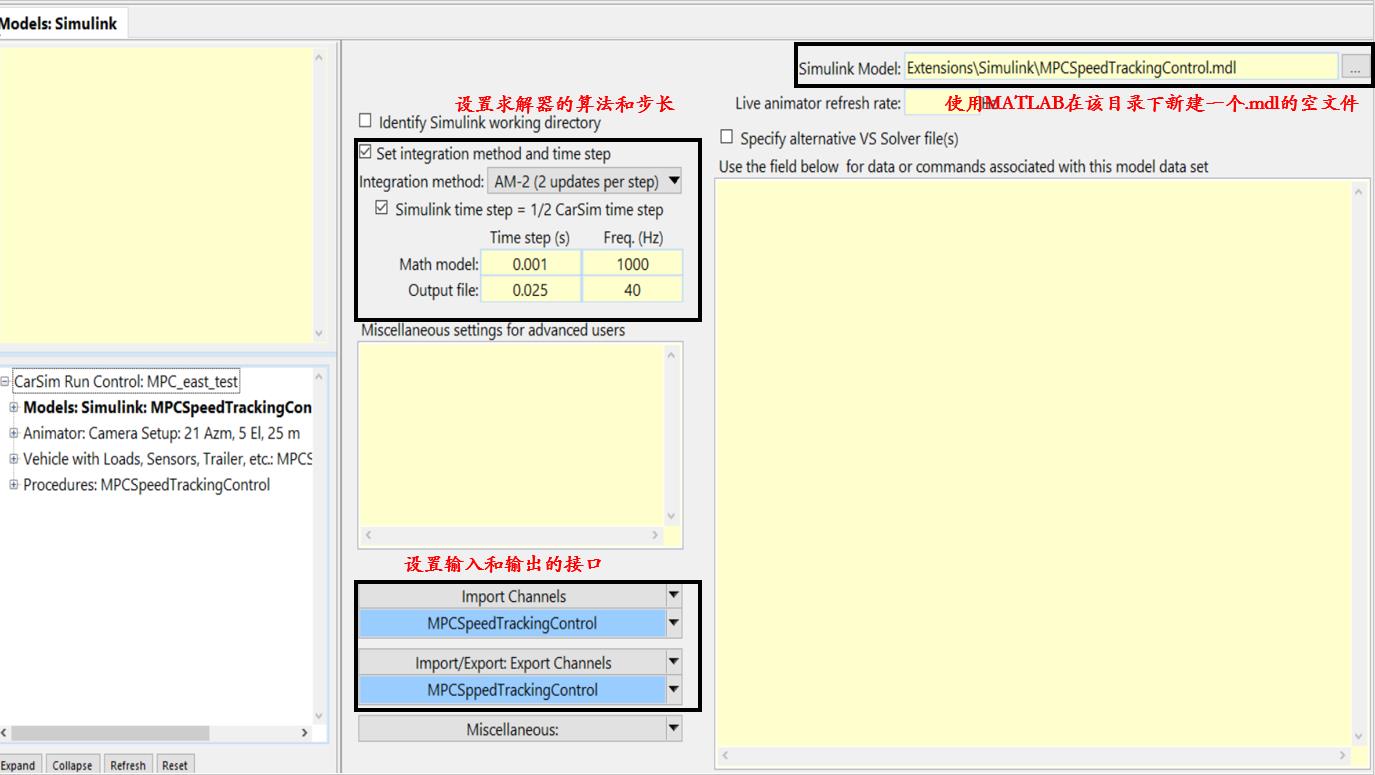
这里的输入设置为IMP_THROTTLE_ENGINE（油门输入）、IMP_PCON_BK制动主缸压力[MPa]。

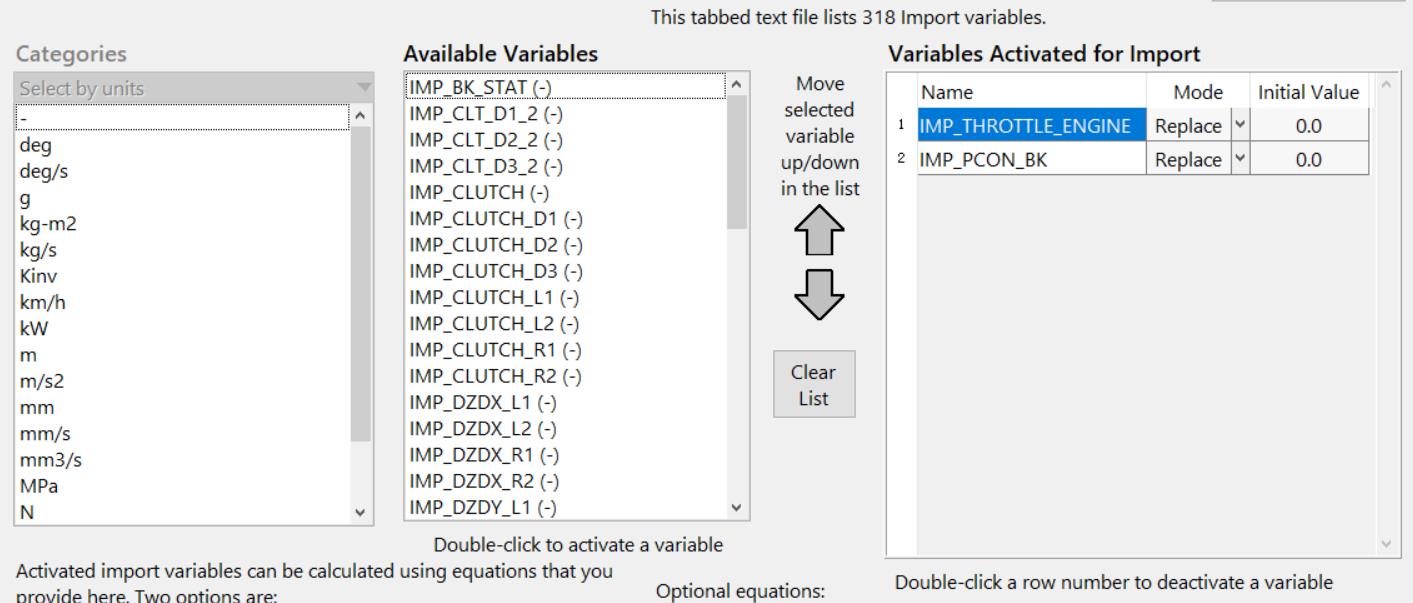
输出设置为车速和加速度：

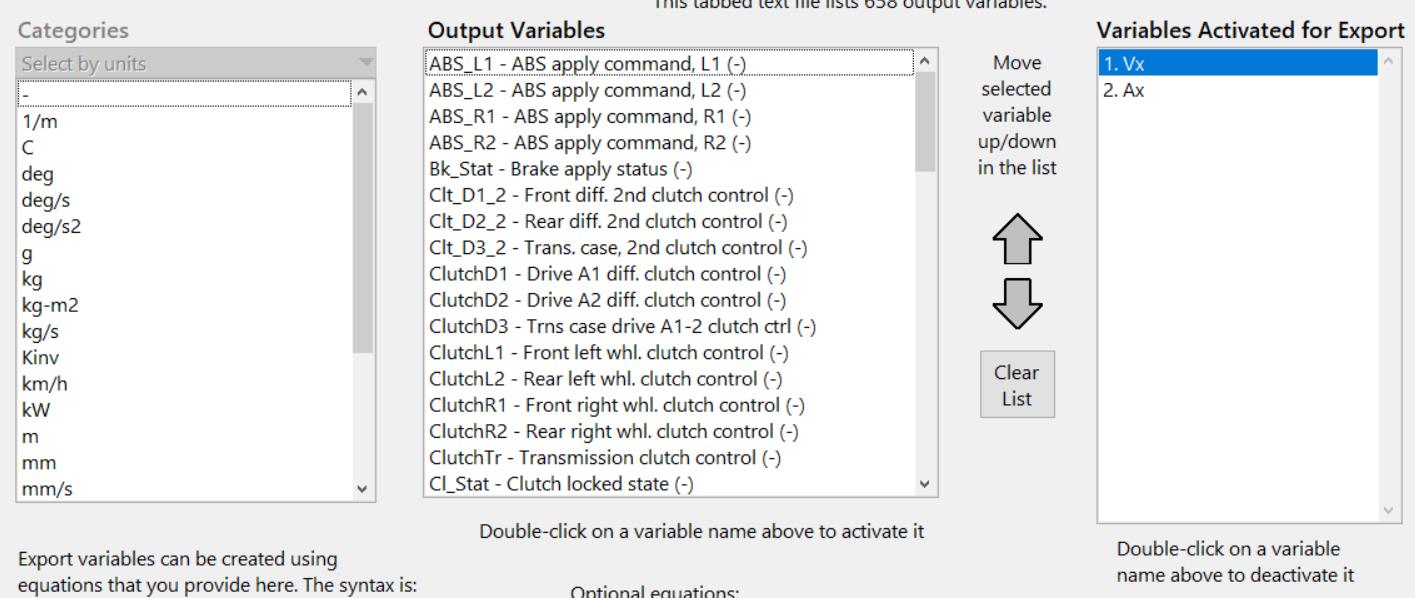
设置好之后点击：Send to Simulink

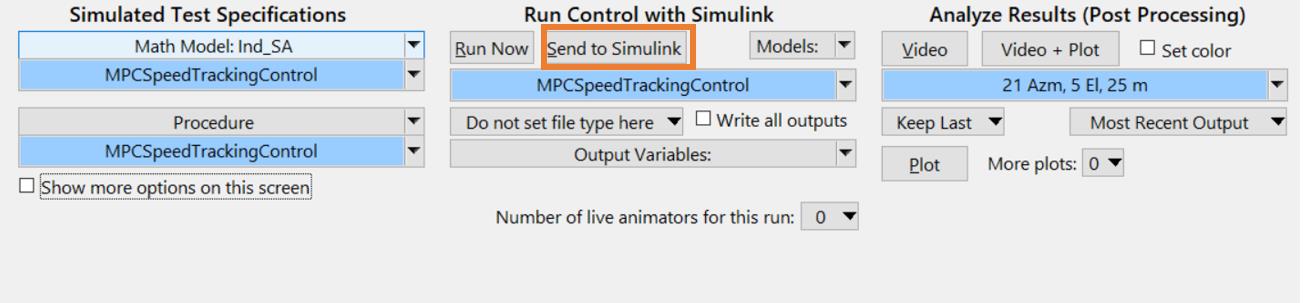
Matlab 框架搭建

在使用Carsim发送过去数据之后，点击MATLAB中的Simulink，此时的Library Browser中应该会出现Carsim S-Function：

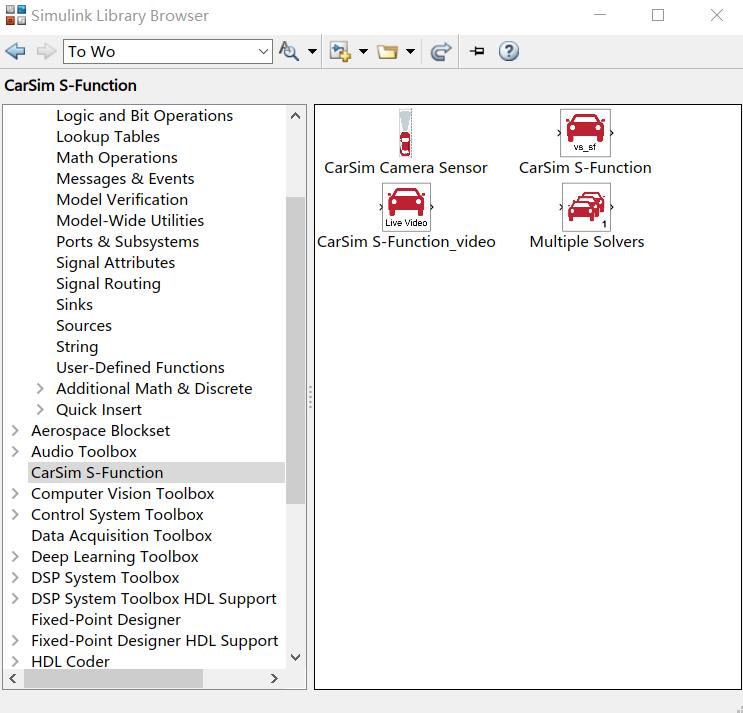
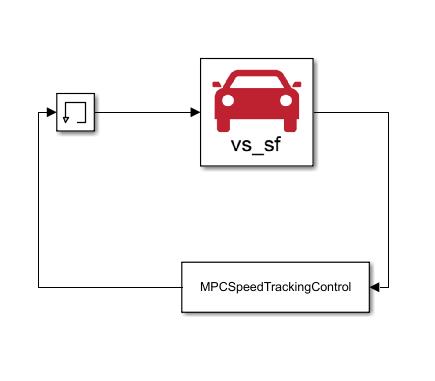
将Carsim S-Functioin拖入Simulink模块，同时在User-Defined Functions中找到S-Function并拖入Simulink模块。构建如下图所示的框架：

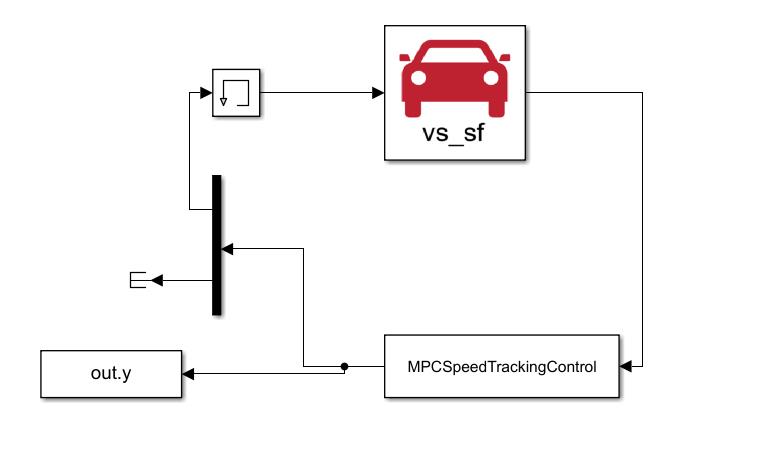
这里稍微解释一下这个框架：
我们希望使用MPC对汽车的速度进行控制。对于MPC，我们的输入是自己设定的期望速度，汽车当前的速度和加速度，这些量暂且统一称为决策变量，根据这些变量，MPC计算之后会给出相应的控制，让汽车去调整到我们期望的速度，这里的控制是油门和制动主缸压力，这样就构成了一个反馈。因为在使用MPC的时候，我们还希望看一些其他量的变化，所以在MPC模块的输出不仅仅是两个控制量，还会有其他的量，使用Terminator模块将不需要输入进Carsim模块终止掉。使用To Workspace模块将MPC所有输出模块导入到MATLAB里面，方便画图。

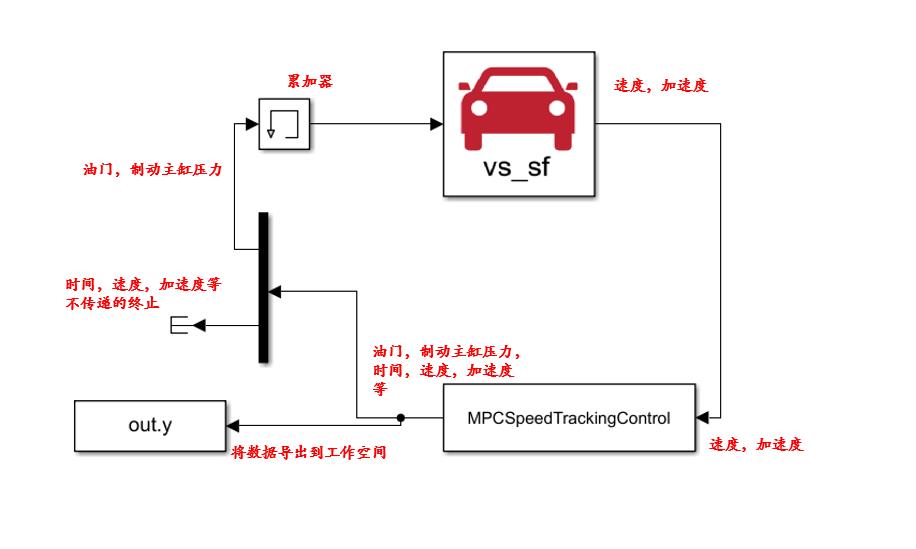
如果不需要看其他参数，可以直接构建如下框架：

MPC速度控制理论

问题描述

汽车的速度控制可以参考下图(来自北理工的书)：其可以分为上位控制器和下位控制器。

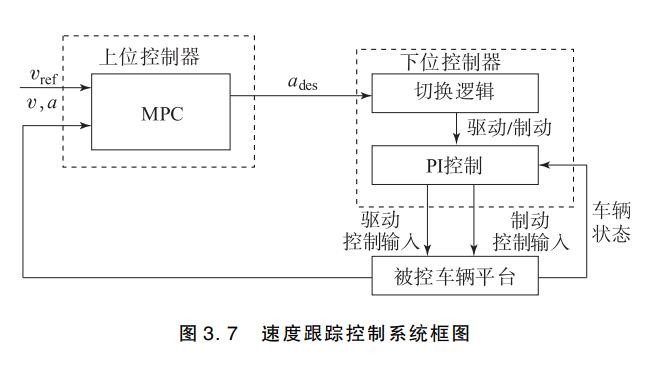
在机器人控制中可以分为底层控制-感知-决策。感知方面其实我们默认是做好的，而且本例也不涉及。这个上位控制可以理解为决策，根据车辆的当前速度加速度状态和期望的速度，判断该如何进行加速度的选择。下位控制器可以理解为底层控制，当车辆做出决策给出应当进行的控制的时候，需要准确的进行这个控制实现。

速度跟踪MPC建模

车辆的纵向控制可以使用一阶惯性系统来表示：
$$\dot{a}=\frac{K}{{\tau }_d}(a_{des}-a)$$
其中$K=1$为系统的增益；${\tau }_d$为时间常数。将上式和速度加速度关系写成矩阵形式，变成状态方程：
$$\dot{x}=Ax+Bu$$
展开表示为：
$$\left(\begin{array}{c}\dot{v}\\ \dot{a}\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 0& \frac{-1}{{\tau }_d}\end{array}\right)\left(\begin{array}{c}v\\ a\end{array}\right)+\left(\begin{array}{c}0\\ \frac{K}{{\tau }_d}\end{array}\right)a_{des}$$
使用前向欧拉法，进行离散：
$$x(k+1)=A_{k}x(k)+B_{k}u(k)$$
展开表示为：
$$\left(\begin{array}{c}v(k+1)\\ a(k+1)\end{array}\right)=\left(\begin{array}{cc}1& T_s\\ 0& 1-\frac{T_s}{{\tau }_d}\end{array}\right)\left(\begin{array}{c}v(k)\\ a(k)\end{array}\right)+\left(\begin{array}{c}0\\ \frac{K{T}_s}{{\tau }_d}\end{array}\right)a_{des}(k)$$
速度$v$作为系统的输出，输出方程可以表示为：
$$y(k)=Cx(k),C=[10]$$
以上就是模型预测控制中的模型建立。

系统的控制目标定义为：速度跟踪精度，同时还要避免过大的加速度和冲击。
$$J=\sum _{i=1}^{N_p}(y_p(k+i|k)-y_{ref}(k+i|k){)}^2+\sum _{i=1}^{N_c}(\Delta u(k+i){)}^2$$
系统的约束为加速度及其变化率；
u m i n ≤ u ( k + i ) ≤ u m a x , i = 0 , 1 , . . . , N e − 1 Δ u m i n ≤ Δ u ( k + i ) ≤ Δ u m a x , i = 0 , 1 , . . . , N c − 1 u_min≤u(k+i)≤u_max,i=0,1,...,N_e-1\\\\[1.5mm] Δu_min≤Δu(k+i)≤Δu_max,i=0,1,...,N_c-1 目录

一、理论基础

二、核心程序

2.1发射信号,采用QPSK调制

2.2自动增益控制（Automatic Gain Control）