决策树之CART算法

Posted 2023-03-29

参考技术A 一、基本概念

1.cart使用基尼系数作为划分标准。基尼系数越小，则不纯度越低，区分的越彻底。

2.假设有k个类别，第k个类别的概率为 ,则基尼系数表达式为：

Gini(p)= (1- )=1-

3.对于样本D，如果根据特征A 的值把样本分为D1,D2两部分，则在特征A条件下，D的基尼系数

Gini(D,A)= Gini(D1)+  Gini(D2)

4.CART建立起来的是二叉树，如果特征A有A1,A2，A3三个类别，CART会考虑把A分成A1,A2 ,A3两组，或者是其他两种情况。由于这次A并没有完全分开，所以下次还有机会在子节点把A2,A3分开.

5.对于连续值的切分.假如有1 2 3 4 5 那么cart会有4个切分点 [1.5  2.5  3.5  4.5]

二.实例推导树的建立过程

1.假设我有以下源数据

序号 天气 周末 促销 销量

1 坏 是 是 高

2 坏 是 是 高

3 坏 是 是 高

4 坏 否 是 高

5 坏 是 是 高

6 坏 否 是 高

7 坏 是 否 高

8 好 是 是 高

9 好 是 否 高

10 好 是 是 高

11 好 是 是 高

12 好 是 是 高

13 好 是 是 高

14 坏 是 是 低

15 好 否 是 高

16 好 否 是 高

17 好 否 是 高

18 好 否 是 高

19 好 否 否 高

20 坏 否 否 低

21 坏 否 是 低

22 坏 否 是 低

23 坏 否 是 低

24 坏 否 否 低

25 坏 是 否 低

26 好 否 是 低

27 好 否 是 低

28 坏 否 否 低

29 坏 否 否 低

30 好 否 否 低

31 坏 是 否 低

32 好 否 是 低

33 好 否 否 低

34 好 否 否 低

该数据集有三个特征  天气  周末   促销

2.为了简化建立树的过程,我将忽略基尼系数与样本个数阀值

2.1  首先计算各个特征值对数据集的基尼系数,公式见---- 基本概念.3

Gini(D|天气)=17/34*(1-(11/17)^2-(6/17)^2)+17/34*(1-(7/17)^2-(10/17)^2)=0.4706

Gini(D|周末)=20/34*(1-(7/20)^2-(13/20)^2)+14/34*(1-(11/14)^2-(3/14)^2)=0.4063

Gini(D|促销)=12/34*(1-(9/12)^2-(3/12)^2)+22/34*(1-(7/22)^2-(15/22)^2)=0.4131

周末的基尼系数最小，这也符合我们的一般认识

2.2  第一个分列特征选择周末。此时数据集按照是否周末分成两个。

Gini(周末|天气)=0.2679

Gini(周末|促销)=0.2714

Gini(非周末|天气)=0.3505

Gini(非周末|促销)=0.3875

此时，周末应该以天气作为划分，非周末也是以天气作为划分，下面放个图

三、CART树对于连续特征的处理

假如特征A为连续型变量，则把特征A按照从小到大进行排序，取相邻两点的平均值为切分点，计算基尼系数。则基尼系数最小的点为切分点，大于切分点的为一类，小于切分点的为另一类。举例：特征A的值为 1，2，3，4，5，6     目标变量是高、低、高、低、高、低。则1.5处的基尼系数为  (1/6)*(1-1^2)+(5/6)*(1-(2/5)^2-(3/5)^2)=0.4                                                2.5处的基尼系数为  (2/6)*(1-(1/2)^2-(1/2)^2)+(4/6)*(1-(2/4)^2-(2/4)^2)=0.5                              3.5处的基尼系数为   (3/6)*(1-(1/3)^2-(2/3)^2)+(3/6)*(1-(1/3)^2-(2/3)^2)=0.44                          4.5处的基尼系数为   (4/6)*(1-(2/4)^2-(2/4)^2)+(2/6)*(1-(1/2)^2-(1/2)^2)=0.5                            5.5处的基尼系数为    (5/6)*(1-(2/5)^2-(3/5)^2)+(1/6)*(1-1^2)=0.4                                          结论：  1.5和5.5处的基尼系数最小，可以把1分为一类，2-6分为另一类。或者6分为一类，1-5另一类。

四、关于回归树

1.回归树和分类树的区别在于输出值类型不同。分类树输出的是离散值，回归树输出的是连续值。

2.和分类树使用基尼系数不同，回归树使用和均方差来度量最佳分隔点。假设有1 2 3 4 5 6 六个数。假设3.5处把数据分开最合适，那么(1-2)^2+(2-2)^2+(3-2)^2+(4-5)^2+(5-5)^2+(6-5)^2在所有分割点中取得最小值。2，5为各自数据段的平均值。

3.回归树采用最后叶子的平均值或者中值作为输出结果

决策树之 ID3 算法

概述

ID3 算法是构建决策树算法中一种非常重要的算法，可以说它是学习决策树算法的基础吧。比如，下一篇博客要说的 C4.5 决策树，就是基于 ID3 上的一个改进算法。还有 CART、随机森林算法，都是后面要讲解的。

---

版权说明

著作权归作者所有。
商业转载请联系作者获得授权，非商业转载请注明出处。
本文作者：Q-WHai
发表日期： 2016年7月6日
本文链接：https://qwhai.blog.csdn.net/article/details/51837983
来源：CSDN
更多内容：分类 >> 数据挖掘

---

引言

如果你是刚刚才接触到有关决策树的相关内容，那么你可能就会有一些疑问，什么是决策树？对于什么是决策树这个话题，如果站在编程的角度来类比，我想 if … else 是最贴切的了吧。就比如下面的这样的一棵最简单的决策树。

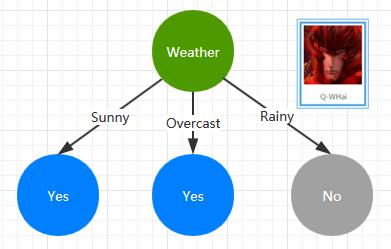
这是一棵是否出门打球的决策树，而决策的特征属性就是 Weather，如果天气状态为 Sunny、Overcast 则选择出门打球；如果下雨了那就只能待在家里了。
如果上面的这棵决策树是按照我的选择来构建的，那么你的选择又会构建成一棵什么样的决策树呢？也就是说某一棵决策树只能代表某一种情况，可是我们是想拿构建好的决策树进行预测的，所以这时，就不能再只按照某一个人的意愿来构建决策树了。我们需要收集大量的训练数据，并使用这些训练数据进行构建决策树。

---

基础知识

数据挖掘的基础是数学，如果数学不太好，就一定要好好补补了（我也是数学不太好的那些人当中的一个）。ID3 算法当然也不例外地涉及了一些数学知识。主要的是两块内容：信息熵与信息增益。

信息熵

信息熵简介

中学时期，我们都有学习过熵的概念，主要是在物理跟化学中。在物理学科中，熵是用来描述分子的混乱程度的，在化学学科中也是类似的，如果我没有记错的话，当时熵在化学中的应用主要是某一化合物的加热这一块，比如给水加热，会变化水蒸汽，这时熵就是增大的；还就是化合反应这一块。
那么在本文的 ID3 算法中，或者说在数据挖掘中的信息熵要怎么理解或是怎么应用呢？这里不妨打个最简单的比方，我们说假设有两篇文章，分别为：Article_1 和 Article_2，它们的内容如下：
Article_1

信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵
信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵
信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵
信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵

Article_2

信息论之父 C. E. Shannon 在 1948 年发表的论文“通信的数学理论（ A Mathematical Theory of Communication ）”中， Shannon 指出，任何信息都存在冗余，冗余大小与信息中每个符号（数字、字母或单词）的出现概率或者说不确定性有关。
Shannon 借鉴了热力学的概念，把信息中排除了冗余后的平均信息量称为“信息熵”，并给出了计算信息熵的数学表达式。

对于上面的这两篇文章，我们要怎么衡量其信息量呢？文章的字数么？显然不是的，第一篇文章的字数要比第二篇文章的字数要多，然而其包含的信息量却要小一些。于是，信息熵的概念就此被引出，结合上面对熵的描述，你也可以理解成信息熵就是信息的混乱程度。

信息熵公式

假如一个随机变量 X 的取值为 X = $x_1,x_1,...,x_n$，每一种取到的概率分别是 $p_1,p_1,...,p_n$，那么 X 的熵定义为
$$H(x)=-\sum _{i=1}^n{p}_{i}lo{g}_2{p}_i$$

信息增益

信息增益简介

信息增益的功能是描述一个特征属性对于总体的重要性，怎么理解这句话呢？打个比方吧，比如我想出去打球，这里可能会受到天气、温度、心情等等的因素地影响。那么对于天气这个特征属性而言，有天气这个属性跟没有天气这个属性，总体的信息量（也就是信息熵）的变化就是信息增益了。
可能这里还不太清楚信息增益在决策树的构建中产生了什么作用，这个问题我们留到 ID3 算法部分再详细说明。

信息增益公式

$$IG(S|T)=Entropy(S)-\sum _{value(T)}\frac{|S_v|}{S}Entropy(S_v)$$
其中 S 为全部样本集合，value(T) 是属性 T 所有取值的集合，v 是 T 的其中一个属性值，$S_v$是 S 中属性 T 的值为 v 的样例集合，$|S_v|$ 为 $S_v$ 中所含样例数。

---

ID3

决策树构建分析

ID3 是数据挖掘中的一种非常重要的决策树构建算法，它是一种监督学习式的机器学习。由于这是一种监督学习，所以必然需要有一定数量的训练数据集，而每一条训练数据所形成的决策树都不一定是完全一样的。打个比方，假设有如下三条训练数据：

Day	OutLook	Temperature	Humidity	Wind	PlayTennis
1	Sunny	Hot	High	Weak	No
2	Sunny	Hot	High	Strong	No
3	Rainy	Mild	High	Weak	Yes

那么对于 OutLook 这一特征属性而言，就有两种不同的状态值：Sunny 和 Rainy。就算是对于同一个 OutLook 状态值时，其结果分类也是一样的，这样我们构建的决策的标准是什么呢？

训练数据集

假设我们如下训练数据集

Day	OutLook	Temperature	Humidity	Wind	PlayTennis
1	Sunny	Hot	High	Weak	No
2	Sunny	Hot	High	Strong	No
3	Overcast	Hot	High	Weak	Yes
4	Rainy	Mild	High	Weak	Yes
5	Rainy	Cool	Normal	Weak	Yes
6	Rainy	Cool	Normal	Strong	No
7	Overcast	Cool	Normal	Strong	Yes
8	Sunny	Mild	High	Weak	No
9	Sunny	Cool	Normal	Weak	Yes
10	Rainy	Mild	Normal	Weak	Yes
11	Sunny	Mild	Normal	Strong	Yes
12	Overcast	Mild	High	Strong	Yes
13	Overcast	Hot	Normal	Weak	Yes
14	Rainy	Mild	High	Strong	No

决策树构建过程

下面是我根据 ID3 构建决策树的算法步骤，绘制的决策树构建过程图。因为 ID3 其实是一个迭代的算法，这里我只绘制了一次迭代的过程，所以是一个局部示图。

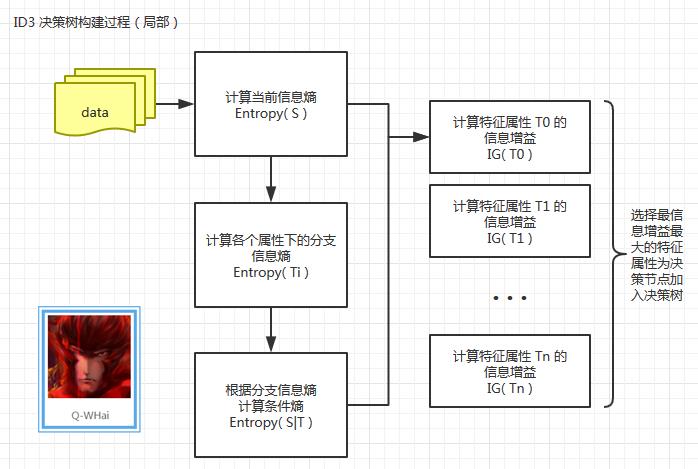
当上面的局部过程中的最后一步计算出了最大信息增益之后，我们要将这个最大信息增益对应的特征属性进行移除，并将数据集切分成 N 个部分（其中 N　为分支状态数）。
现在假设我们计算出当选择特征属性为 OutLook 的时候，其信息增益最大，那么原始数据就会被切分成如下 3 份：
part_sunny

Day	Temperature	Humidity	Wind	PlayTennis
1	Hot	High	Weak	No
2	Hot	High	Strong	No
3	Mild	High	Weak	No
4	Cool	Normal	Weak	Yes
5	Mild	Normal	Strong	Yes

part_overcast

Day	Temperature	Humidity	Wind	PlayTennis
1	Hot	High	Weak	Yes
2	Cool	Normal	Strong	Yes
3	Mild	High	Strong	Yes
4	Hot	Normal	Weak	Yes

part_rainy

Day	Temperature	Humidity	Wind	PlayTennis
1	Mild	High	Weak	Yes
2	Cool	Normal	Weak	Yes
3	Cool	Normal	Strong	No
4	Mild	Normal	Weak	Yes
5	Mild	High	Strong	No

这样再把这 3 份数据分别当成上图中的 data 代入计算。通过这样循环地迭代，直到数据被全部计算完成。

计算步骤

如果上面信息熵跟信息增益的计算公式，让你看得有一些不是很懂，没关系。这里我会通过几个示例来分析一下计算过程，这样你就会更懂一些了。

1. Entropy(S)
2. Entropy($T_i$)
3. Entropy(S|T)
4. IG(T)

Entropy(S)

对于最初始的 14 条记录，我们统计了结果分类，其中，Yes = 9，No = 5.
这时当前信息的信息熵计算过程如下：
$ Entropy(S) = -\\frac914 log_2\\frac914 - \\frac514 log_2\\frac514 = 0.940286 $

Entropy($T_i$)

假设这时我们需要计算最初始的 14 条记录中，特征属性为 OutLook 的分支状态信息熵。首先需要做的是，统计 OutLook 特征属性下的结果分类分布。

	Sunny	Overcast	Rainy
Yes	2	4	3
No	3	0	2

各个特征属性下的分支状态信息熵计算过程如下：
$ Entropy(Sunny) = -\\frac25 log_2\\frac25 - \\frac35 log_2\\frac35 = 0.970951 $
$ Entropy(Overcast) = -\\frac44 log_2\\frac44 - \\frac04 log_2\\frac04 = 0 $
$ Entropy(Rainy) = -\\frac35 log_2\\frac35 - \\frac25 log_2\\frac25 = 0.970951 $

Entropy(S|T)

统计完各个分支状态的信息熵之后，就需求合并，也就是某一特征属性的信息熵了。
$ Entropy(S|OutLook) = \\frac514*Entropy(Sunny) + \\frac414*Entropy(Overcast) + \\frac514*Entropy(Rainy) = 0.693536 $

IG(T)

我们还是拿上面的数据进行计算。也就是计算 IG(OutLook).
$ IG(OutLook) = Entropy(S) - Entropy(S|OutLook) = 0.940286 - 0.693536 = 0.24675 $

决策树构建结果

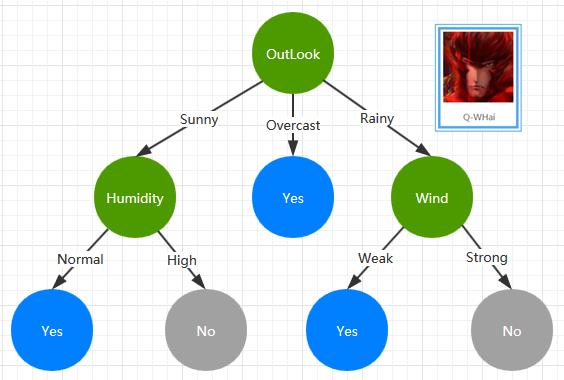
通过上面的训练数据集及 ID3 构建算法，我们构建了一棵如下的 ID3 决策树。

Ref

• http://blog.csdn.net/acdreamers/article/details/44661149
• http://www.cnblogs.com/leoo2sk/archive/2010/09/19/decision-tree.html

GitHub download

此处为本文的算法实现，采用的编程语言为 Java。算法也是在不断重构及优化，如果你对此感兴趣，欢迎 star.

• https://github.com/MachineLeanring/MachineLearningID3

征集

如果你也需要使用ProcessOn这款在线绘图工具，可以使用如下邀请链接进行注册：
https://www.processon.com/i/56205c2ee4b0f6ed10838a6d