备战数学建模18-数据插值和曲线拟合2

Posted 2022-05-11 nuist__NJUPT

目录

一、数据插值

1-插值的概念和基本应用

2-MATLAB一维插值

3-MATLAB二维插值

二、曲线拟合

1-拟合问题

2-拟合的计算与MATLAB实现

---

一、数据插值

1-插值的概念和基本应用

我们先通过下面的几个例子去了解一下数据插值，对于例子1，我们只有偶数点的环境温度，可以通过数据插值的方式得到奇数点的环境温度，并做出24小时环境温度的曲线图。

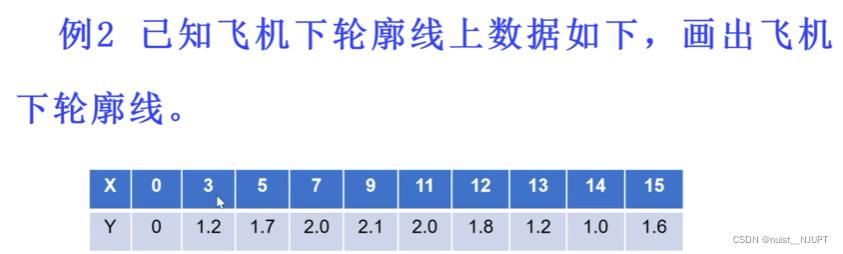
对于例子2，我们可以发现由已知的离散数据点很难画出轮廓线，我们可以通过插值的方法使得数据点更加的紧密，根据紧密的数据点画出轮廓线。

 

 

 

 

2-MATLAB一维插值

对于上面的例子1，我们给出的MATLAB插值代码如下所示：

clear; clc
x = 0 : 2 : 24 ;
y = [12, 9, 9, 10, 18, 24, 28, 27, 25, 20, 18, 15, 13] ;
x1 = 13 ;
y1 = interp1(x,y,x1,'spline') ;
disp('下午一点的温度如下：') ;
disp(y1) ;
xi = 0 : 1/3600 : 24 ;
yi = interp1(x,y,xi,'spline') ;
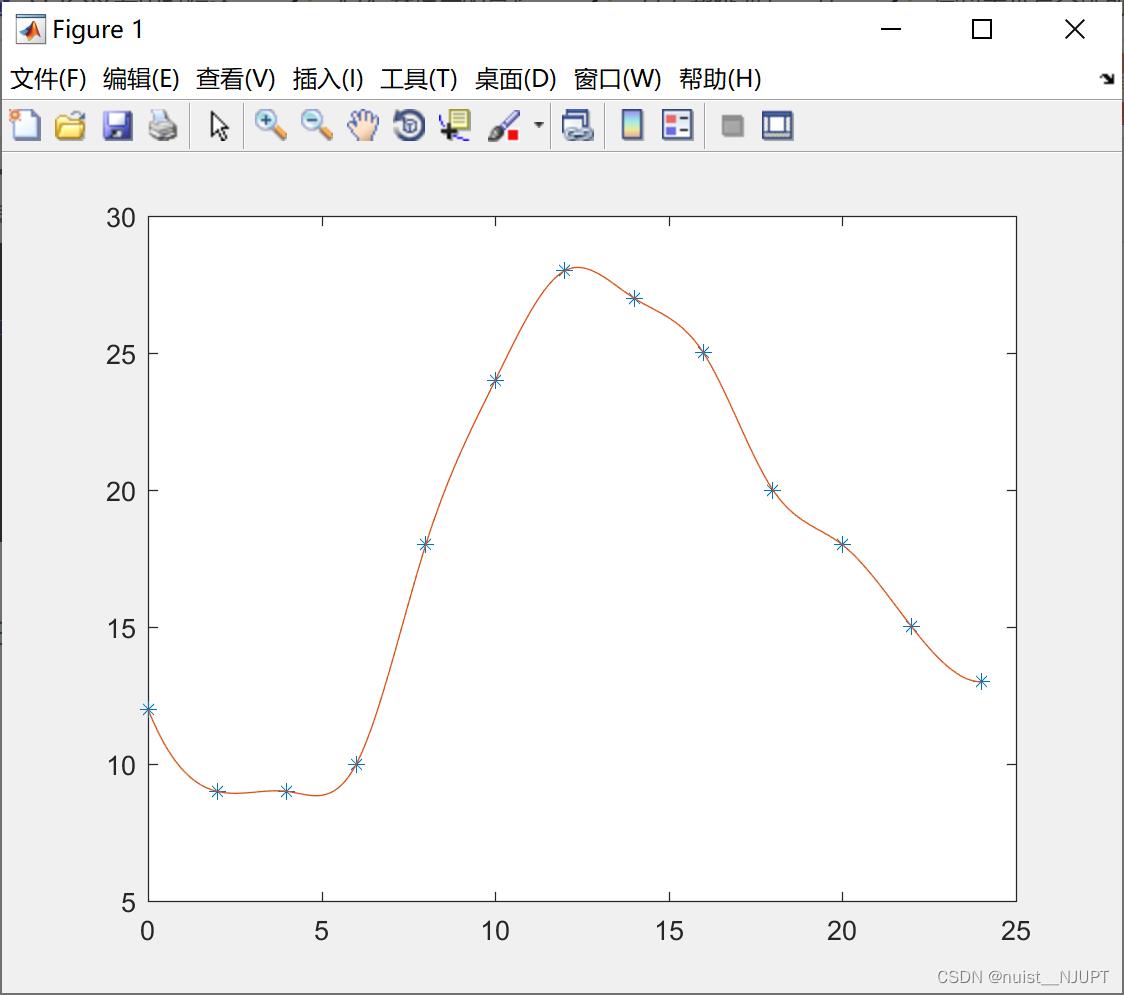
plot(x,y,'*',xi,yi) ;

下午1点的温度和绘制的曲线图如下所示：

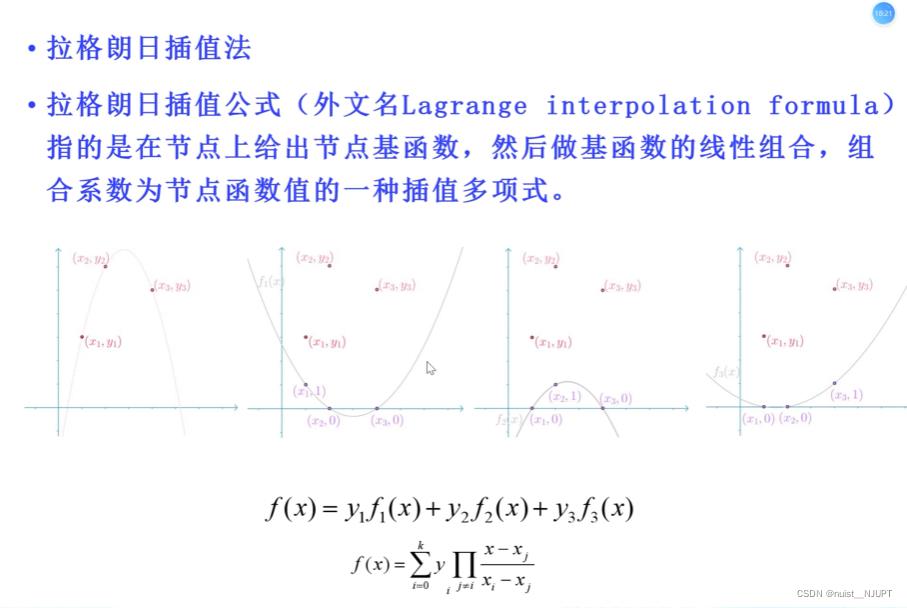
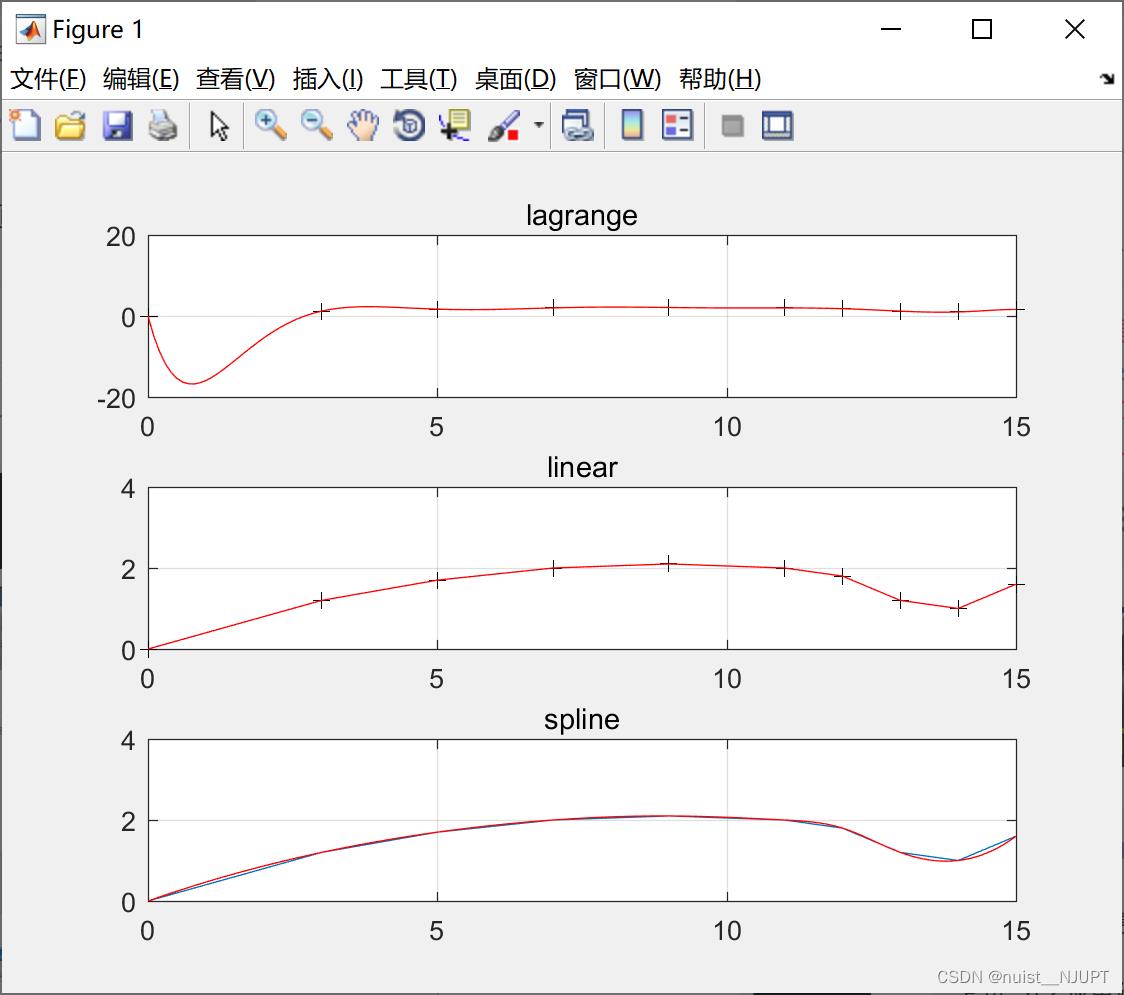
对于例子2，我们分别使用拉格朗日插值，线性插值和三次样条插值实现，MATLAB代码如下：

clear; clc
x0 = [0, 3, 5, 7, 9, 11, 12, 13, 14, 15] ;
y0 = [0, 1.2, 1.7, 2.0, 2.1, 2.0, 1.8, 1.2, 1.0, 1.6] ;
x = 0 : 0.1 : 15 ;
y1 = lagrange(x0, y0, x) ; %拉格朗日插值
y2 = interp1(x0, y0, x) ; %线性插值
y3 = interp1(x0,y0,x,'spline') ; %三次样条插值
subplot(3,1,1) ;
plot(x0,y0,'k+',x,y1,'r') ;
grid on ;
title('lagrange') ;
subplot(3,1,2) ;
plot(x0,y0,'k+',x,y2,'r') ;
grid on ;
title('linear') ;
subplot(3,1,3) ;
plot(x0,y0,x,y3,'r') ;
grid on ;
title('spline') ;

拉格朗日函数lagrange.m,函数如下：

function y = lagrange(x0, y0, x)
n = length(x0) ;
m = length(x) ;
for i = 1 : m
    z = x(i) ;
    s = 0.0 ;
    for k = 1 : n
        p = 1.0 ;
        for j = 1 : n
            if j ~= k
                p = p * (z - x0(j)) / (x0(k) - x0(j)) ;
            end
        end
        s = p * y0(k) + s ;
    end 
    y(i) = s ;
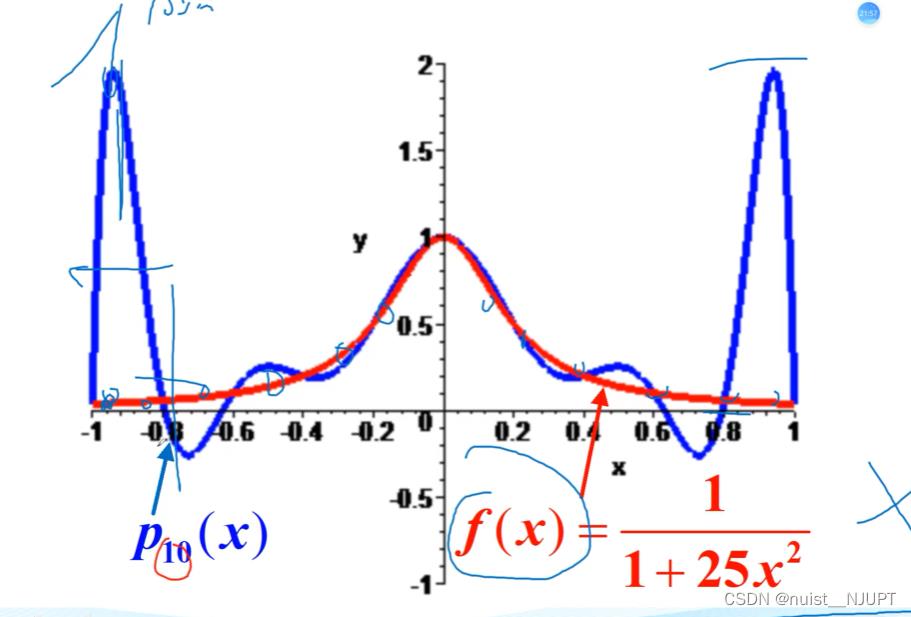
end

运行的结果如下所示。拉格朗日插值在边缘部分出现了龙格现象，一般用的不多，线性插值和三次样条插值好一点，但是三次样条插值更加光滑。

3-MATLAB二维插值

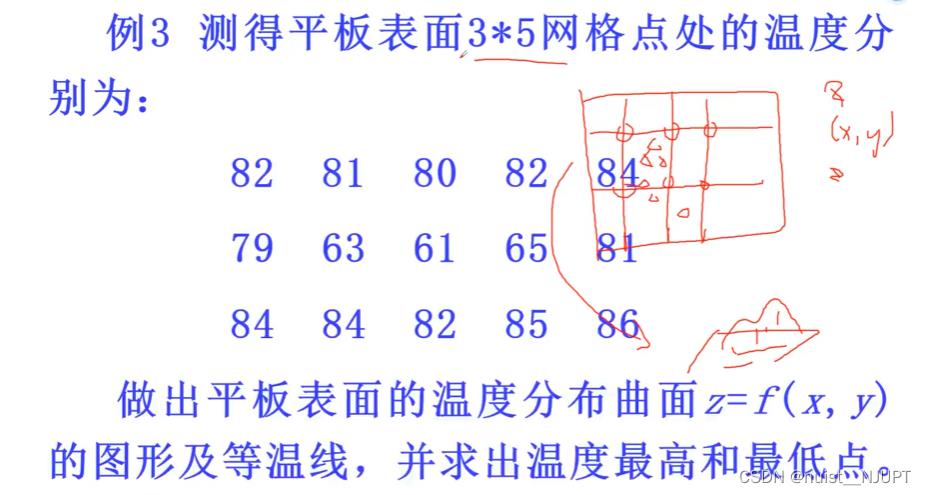
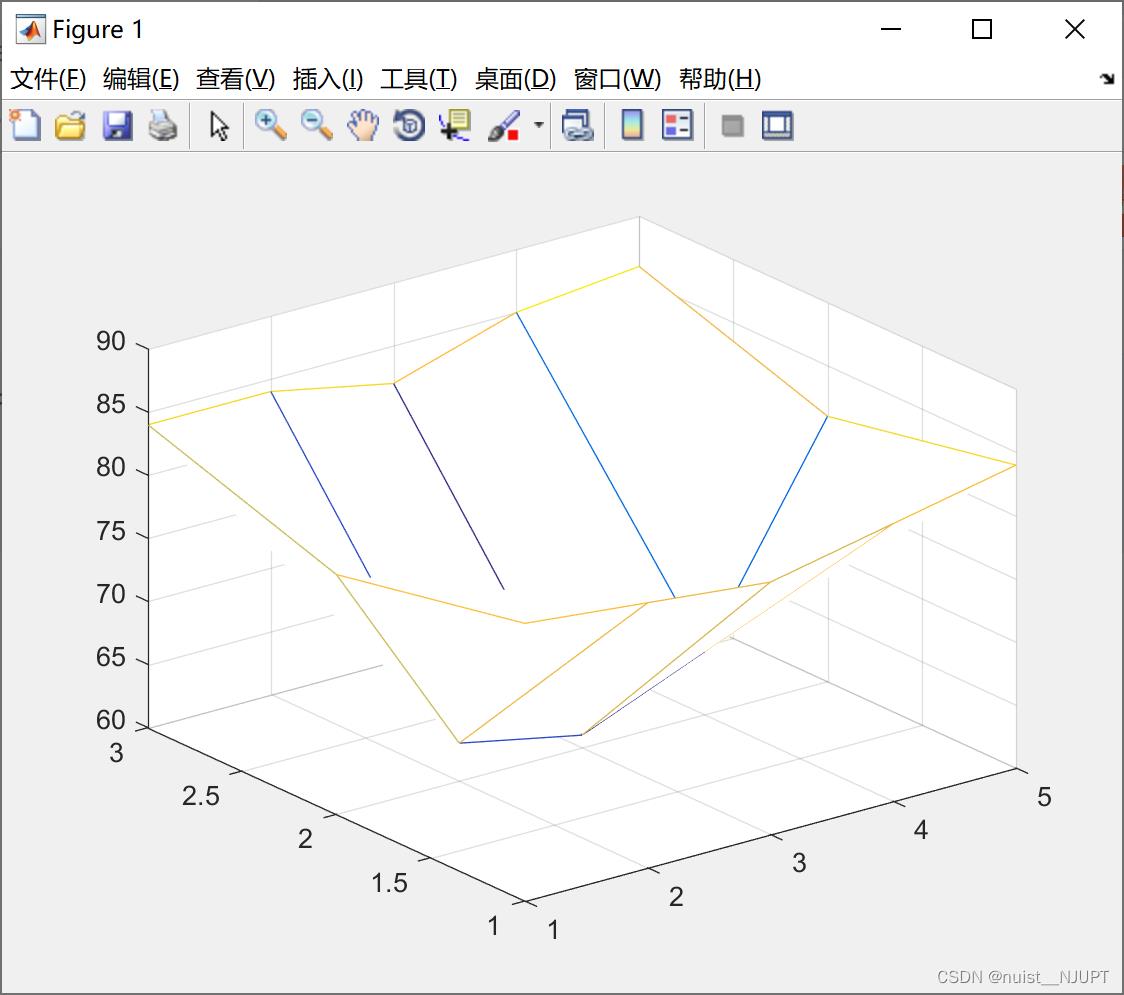
对于例子3，给出的MATLAB插值程序如下所示：

clear; clc
x = 1 : 5 ;
y = 1 : 3 ;
temps = [82, 81, 80, 82, 84; 79, 63, 61, 65, 81; 84, 84, 82, 85, 86] ;
figure(1) ;
mesh(x,y,temps) ; %绘制三维网格图
xi = 1 : 0.2 : 5 ;
yi = 1 : 0.2 : 3 ;
zi = interp2(x,y,temps,xi,yi','cubic') ; %双三次插值
figure(2) ;
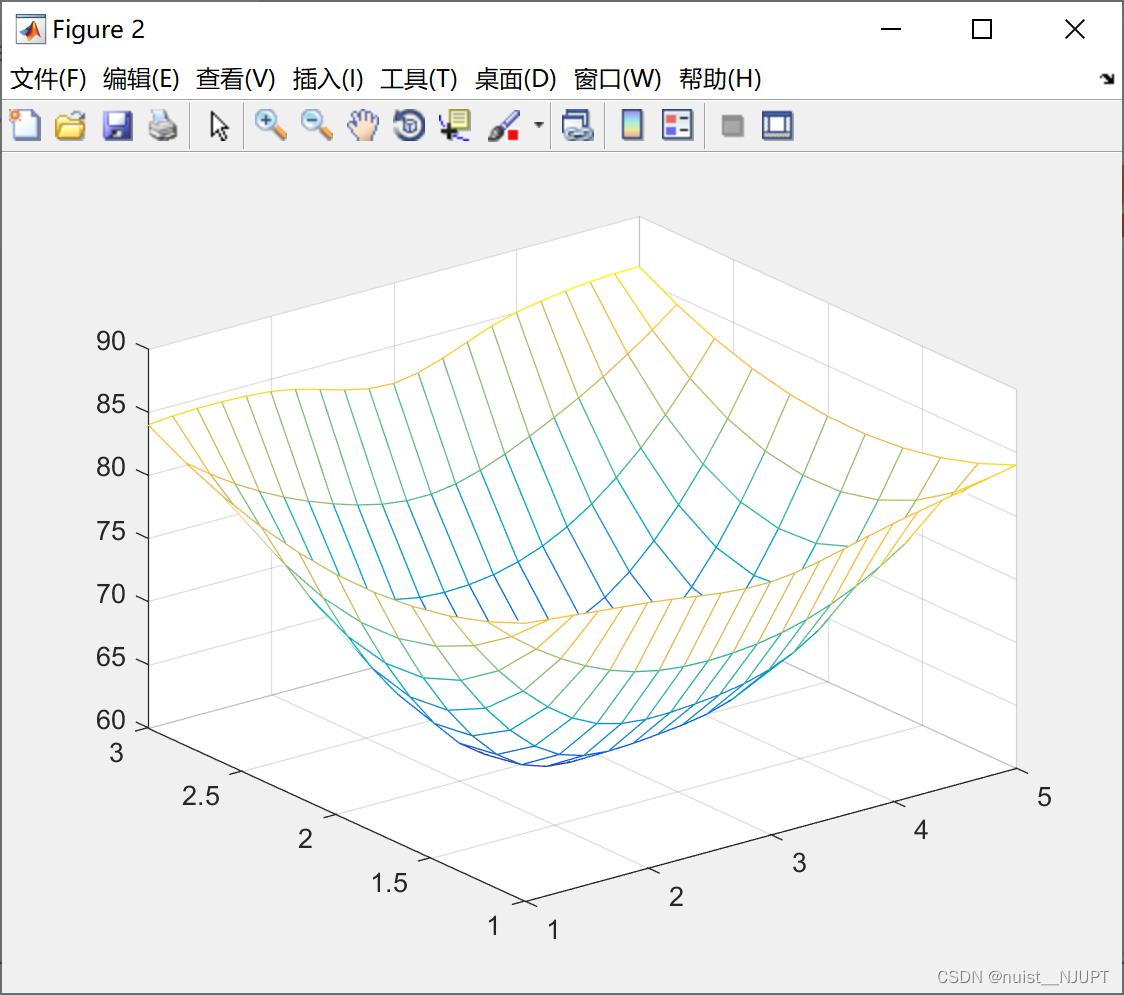
mesh(xi,yi,zi) ;%绘制插值后的网格线图
figure(3) ;
contour(xi,yi,zi,20,'r') ; %画20条等高线
[i,j] = find(zi==min(min(zi))) ;
x = xi(j) ;
y = yi(i) ;
zmin = zi(i,j) ;
disp('温度最低点：') ;
disp(zmin)
[i,j] = find(zi==max(max(zi))) ;
x = xi(j) ;
y = yi(i) ;
zmax = zi(i,j) ;
disp('温度最高点：') ;
disp(zmax) ;

 

运行结果如下所示：

 

 

 

对于上面的例子4，这边给出的MATLAB程序如下：

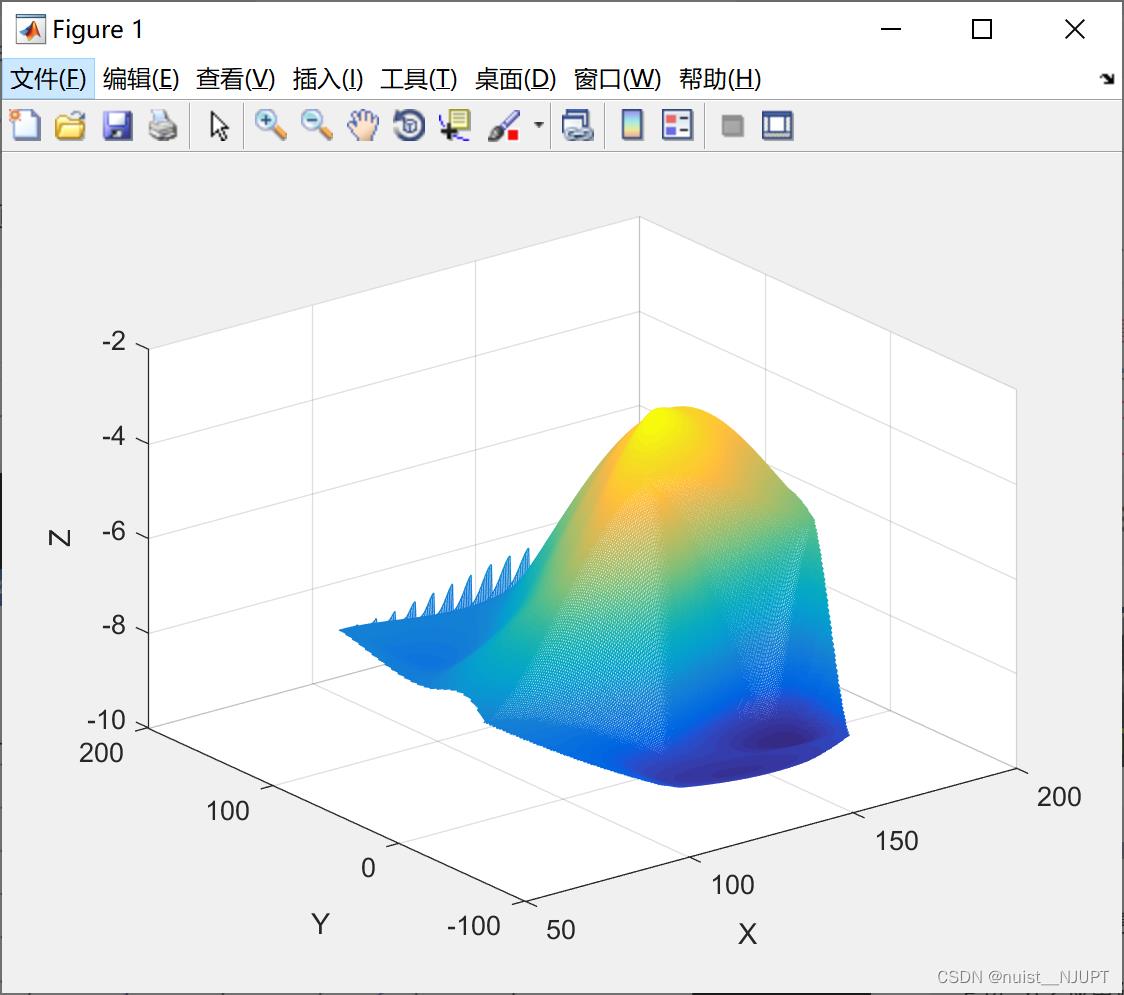
对于上面的例子5，MATLAB的散乱点插值的程序如下所示：

咱们找出水深大于5的才不会搁浅，水深小于5的区域要避免经过。

clear; clc
x = [129, 140, 103.5, 88, 185.5, 195, 105.5, 157.5, 107.5, 77, 81, 162, 162, 117.5] ;
y = [7.5, 141.5, 23, 147, 22.5, 137.5, 85.5, -6.5, -81, 3, 56.5, -66.5, 84, -33.5] ;
z = [-4, -8, -6, -8, -6, -8, -8, -9, -9, -8, -8, -9, -4, -9] ;
[xi, yi] = meshgrid(75 : 0.5 : 200, -70 : 0.5 : 150) ;
zi = griddata(x,y,z,xi,yi,'cubic') ; %散乱点立方插值
figure(1) ;
mesh(xi,yi,zi) ; %画出网格图
xlabel('X') ;
ylabel('Y') ;
zlabel('Z') ;
figure(2) ;
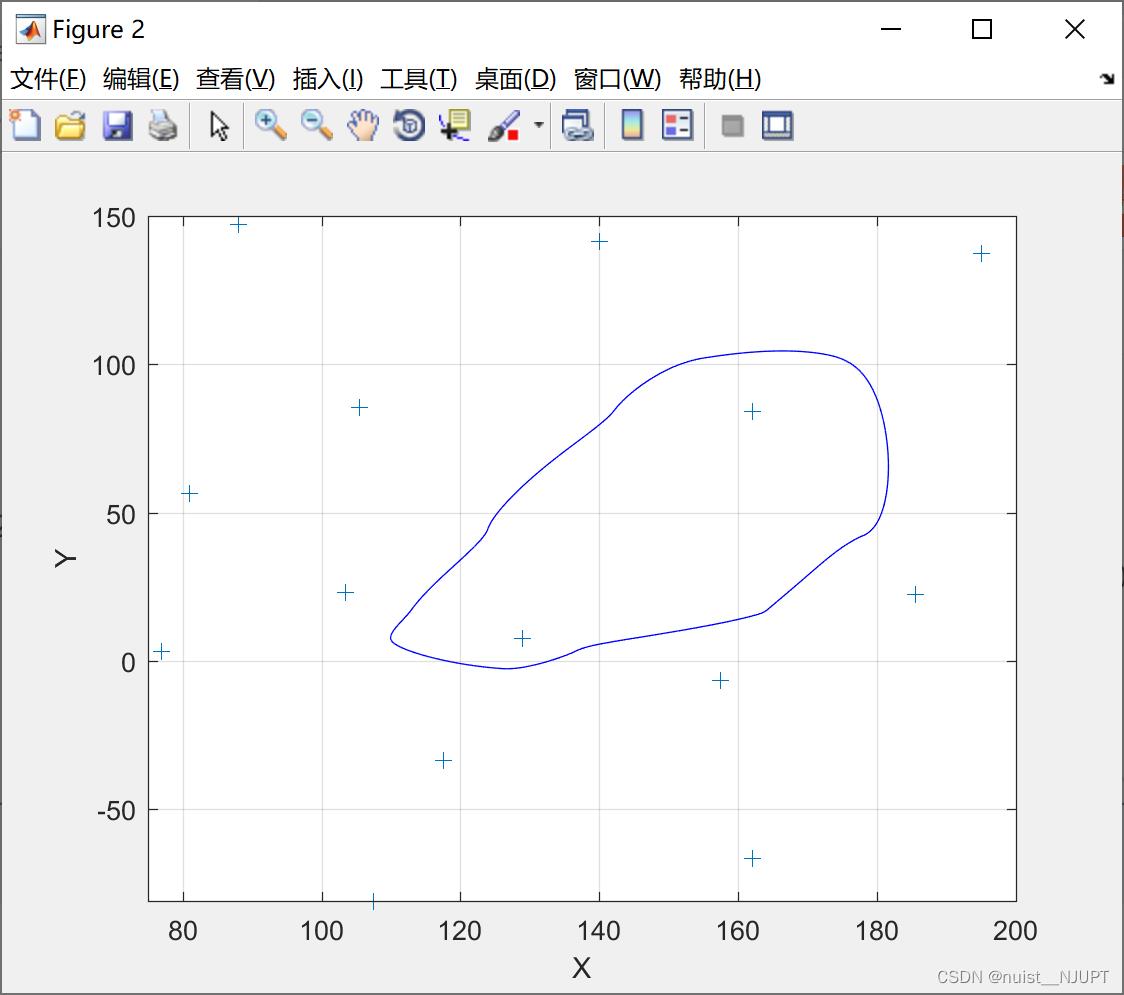
contour(xi, yi, zi, [-5, -5], 'b') ; %找出等高线
grid on ;
hold on ;
plot(x,y,'+') ;
xlabel('X') ;
ylabel('Y') ;

 

运行结果如下所示：图1是海底的地形图，图2是等高线图，区域内是容易搁浅的。

二、曲线拟合

1-拟合问题

我们呢看一下例1，第1小问明显是一个插值问题，而第2小问的数据超出已知数据，我们可以采用曲线拟合的方式进行预测。

 

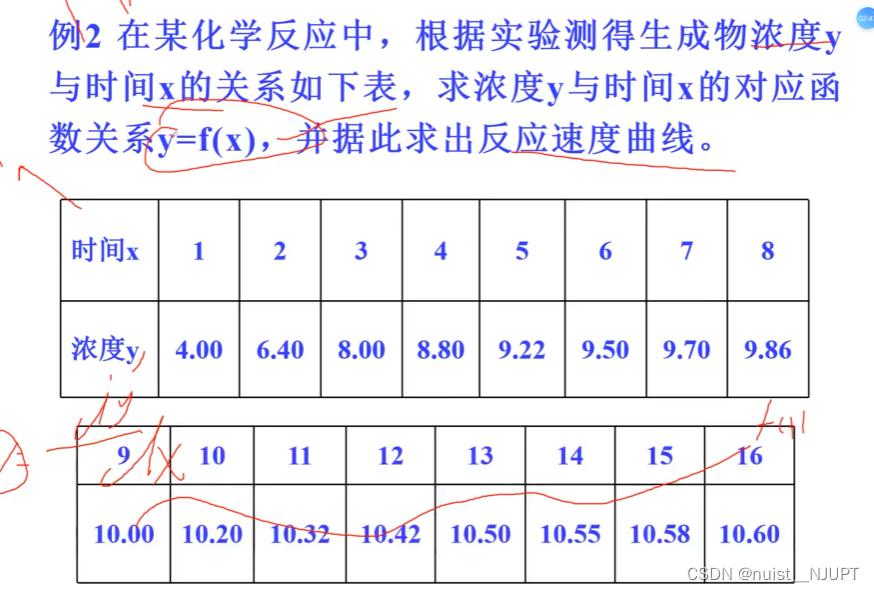
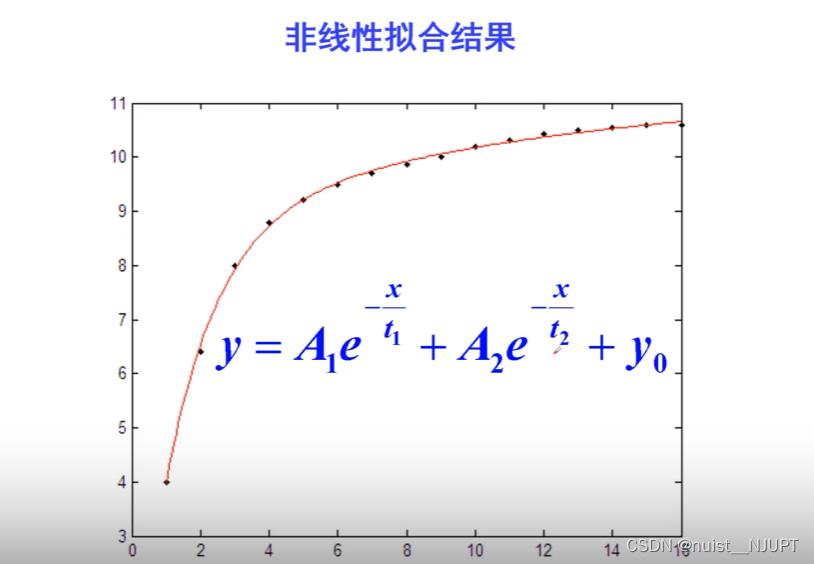
再看一下上面的例子2，可以根据浓度和时间的关系，做出拟合曲线，即反应速度曲线。 

2-拟合的计算与MATLAB实现

我们看下这个简单的MATLAB程序，对x,y做9次多项式拟合得到系数向量a，对于xp求出对于多项式a的值yp，根据xp,yp做出拟合曲线。根据x,y绘制散点图。 

 我们看下面的代码，对于多项式y1,初值为b0,进行非线性拟合，根据拟合的函数a和xp求出对应的函数值yp，然后根据x,y绘制散点图，根据xp,yp绘制拟合曲线。

 

总结一下：一维插值优先选择样条插值，二维插值优先选择立方插值，插值必过已知点，插值仅适用于对已知区间内部数据点的插值，不能超出区间。

拟合不一定过已知点，拟合是根据离散数据求出近似函数，然后进行预测，拟合适用于对于小样本，适合对未来很小得范围做预测。