ACM入门之dfs序列

Posted 2022-05-06 辉小歌

DFS 序列是指 DFS 调用过程中访问的节点编号的序列。
我们发现，每个子树都对应 DFS 序列中的连续一段（一段区间）。

如图所示：

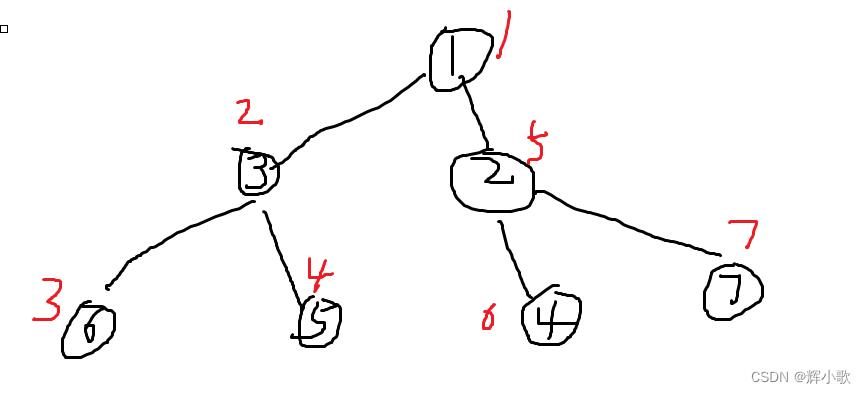
红色的编号便是DFS序列的顺序。你可以很容易的理解就是我们平常的DFS遍历树时，到各个点的顺序。

你会发现以3号结点为子树的序号是连续的。2、3、4。它是连续的。
根据这一性质我们便可以将树转化成区间，来进行一些操作。

具体操作如下：
我们可以引入一个时间戳的概念。in[u] 表示第一次到达u结点的时间 out[u] 表示将u结点的子树遍历完出来的时间
此时以u号结点为例，u结点所有子树的权值和便等于区间[in[u],out[u]]之间的和。

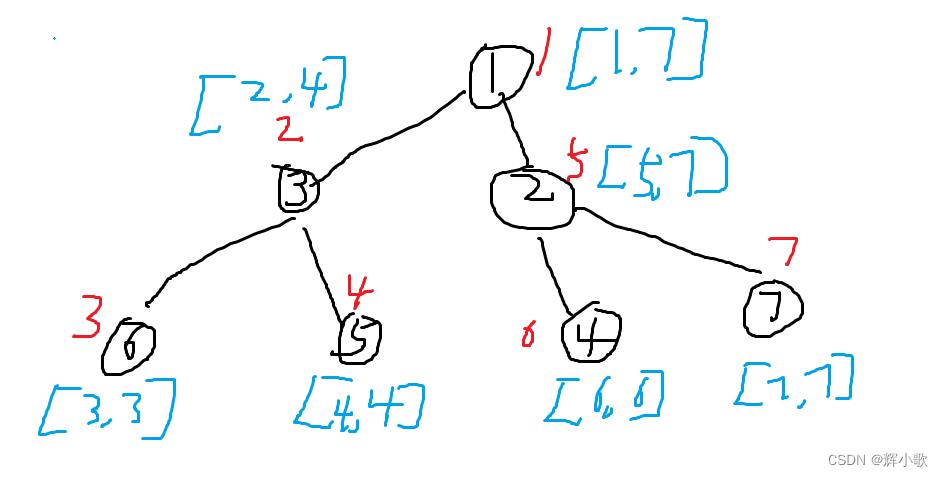
将树变成区间操作之后，我们便可以用处理区间操作的数据结构来搞了。
例如: 用树状数组或线段树来搞。
例题：

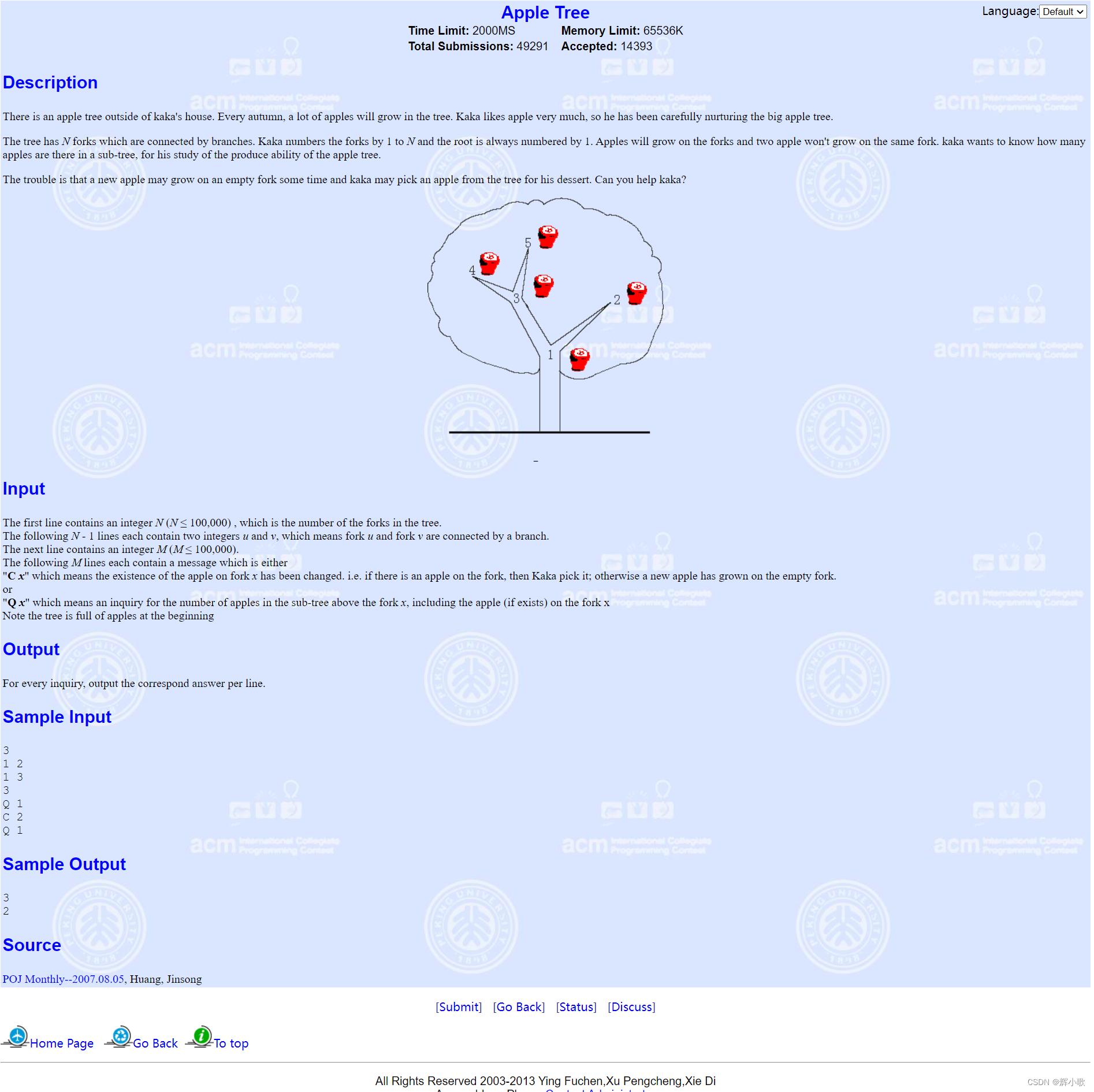
这道题的意思就是: 单点的权值进行修改，求子树的权值和。
这里就用上述方法转为区间，然后用树状数组来求。
http://poj.org/problem?id=3321

#include<iostream> 
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
using namespace std;
const int N=1e6+10;
int h[N],e[N],ne[N],idx;
int in[N],out[N],timestep;//进入的时间  退出的时间  时间戳 
int n,m,st[N],tr[N];
void add(int a,int b)

	e[idx]=b,ne[idx]=h[a],h[a]=idx++;

void dfs(int u,int fa)

	in[u]=++timestep;//进入的时间戳 
	for(int i=h[u];i!=-1;i=ne[i])
	
		int j=e[i];
		if(j==fa) continue;
		dfs(j,u);
	
	out[u]=timestep;//遍历完所有的子树退出的时间戳 

int lowbit(int x)return x&(-x);
void update(int x,int c)

	for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;

int query(int x)

	int sum=0;
	for(int i=x;i;i-=lowbit(i)) sum+=tr[i];
	return sum;

void init()

	memset(h,-1,sizeof h);
	memset(tr,0,sizeof tr);
	idx=0;
	timestep=0;

int main(void)

	while(scanf("%d",&n)!=EOF)
	
		init();
		for(int i=1;i<=n-1;i++)
		
			int a,b; scanf("%d%d",&a,&b);
			add(a,b),add(b,a); 
		
		dfs(1,-1);
		for(int i=1;i<=n;i++) //初始化 
		
			st[i]=1;//这个点有值 
			update(in[i],1);//树状数组初始化赋值 
		
		scanf("%d",&m);
		while(m--)
		
			char op; 
			int x;
			scanf(" %c%d",&op,&x);
			if(op=='Q')
			
				printf("%d\\n",query(out[x])-query(in[x]-1));//查询 
			
			else 
			
				if(st[x]) update(in[x],-1),st[x]=0;//单点修改  
				else update(in[x],1),st[x]=1;
			
		
	
	return 0;

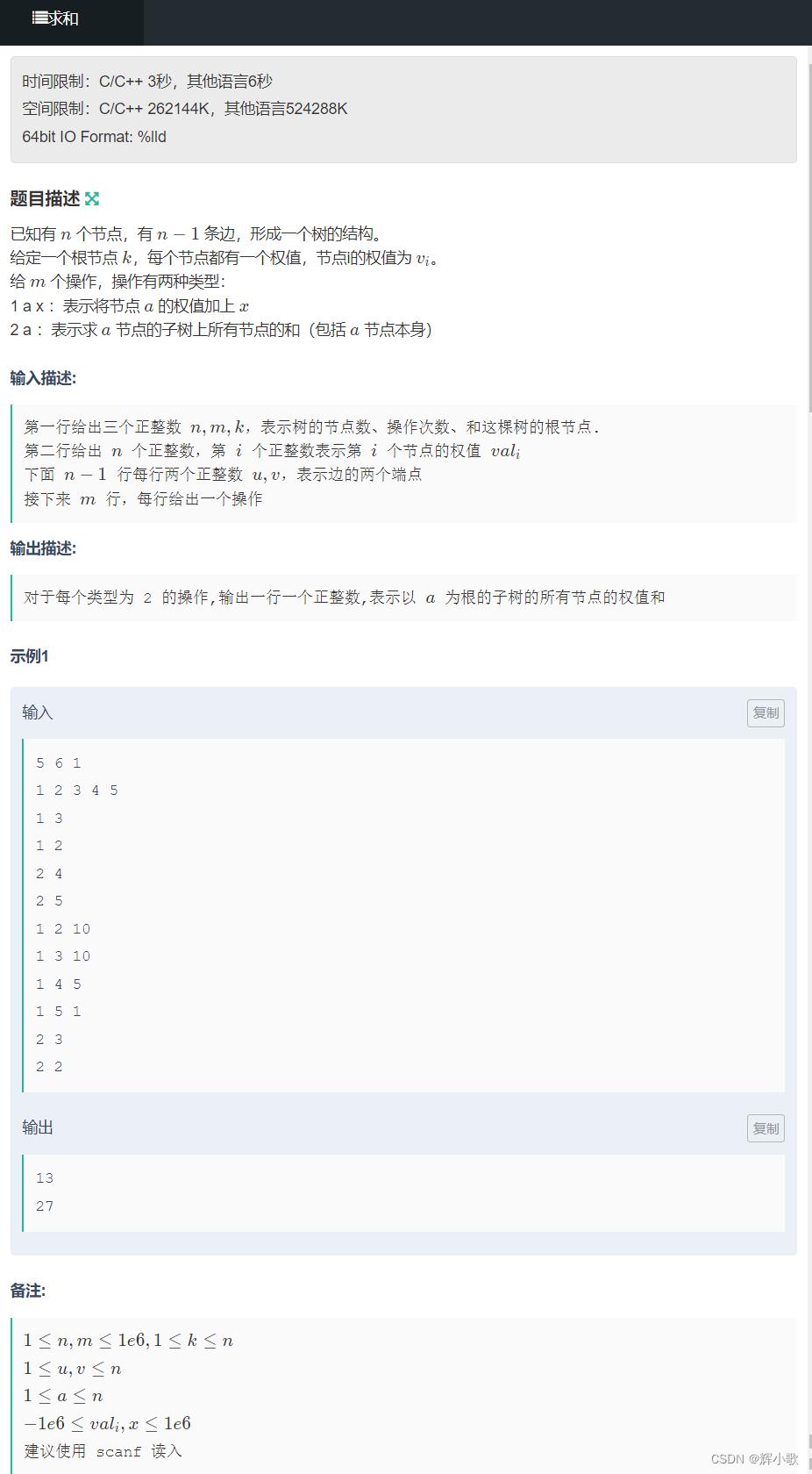
例题二：

#include<bits/stdc++.h> 
using namespace std;
typedef long long int LL;
const int N=1e6+10;
const int M=1e6*2+10;
LL h[N],e[M],ne[M],idx;
LL tr[N],in[N],out[N],w[N],timestep;
int n,m,root;
void add(int a,int b)

	e[idx]=b,ne[idx]=h[a],h[a]=idx++;

void dfs(int u,int fa)

	in[u]=++timestep;
	for(int i=h[u];i!=-1;i=ne[i])
	
		int j=e[i];
		if(j==fa) continue;
		dfs(j,u);
	
	out[u]=timestep;

int lowbit(int x)return x&(-x);
void update(int x,LL v)

	for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=v;

LL query(int x)

	LL sum=0;
	for(int i=x;i;i-=lowbit(i)) sum+=tr[i];
	return sum;

int main(void)

	memset(h,-1,sizeof h);
	scanf("%d%d%d",&n,&m,&root);
	for(int i=1;i<=n;i++) scanf("%lld",&w[i]);
	for(int i=1;i<=n-1;i++)
	
		int a,b; scanf("%d%d",&a,&b);
		add(a,b),add(b,a); 
	
	dfs(root,-1);
	for(int i=1;i<=n;i++) update(in[i],w[i]);//in[i] i号结点在dfs序列中的位置
	while(m--)
	
		int op; scanf("%d",&op);
		if(op==1)
		
			LL u,x; scanf("%lld%lld",&u,&x);
			update(in[u],x);
		else 
		
			LL u; scanf("%lld",&u);
			printf("%lld\\n",query(out[u])-query(in[u]-1));
		
	
	return 0;

这只是DFS序列的入门使用。常用的是和树链剖分相互结合使用。