ACM入门之分层图

Posted 2022-04-29 辉小歌

啥是分层图？
感觉目前关于分层图的详细讲解挺少的。
主要是因为它相对于其他的图论知识是易懂的。

分成图主要解决的问题: 例如:一些特殊标记的边不可选超过k的情况下的最短路。
我们平常的图是二维的,而分层图则是复制k层的图，使得其是三维的。
根据例题来看，你会快速的上手。看例题的代码你会发现，它在最短路上只是多了一点东西。
例题一：

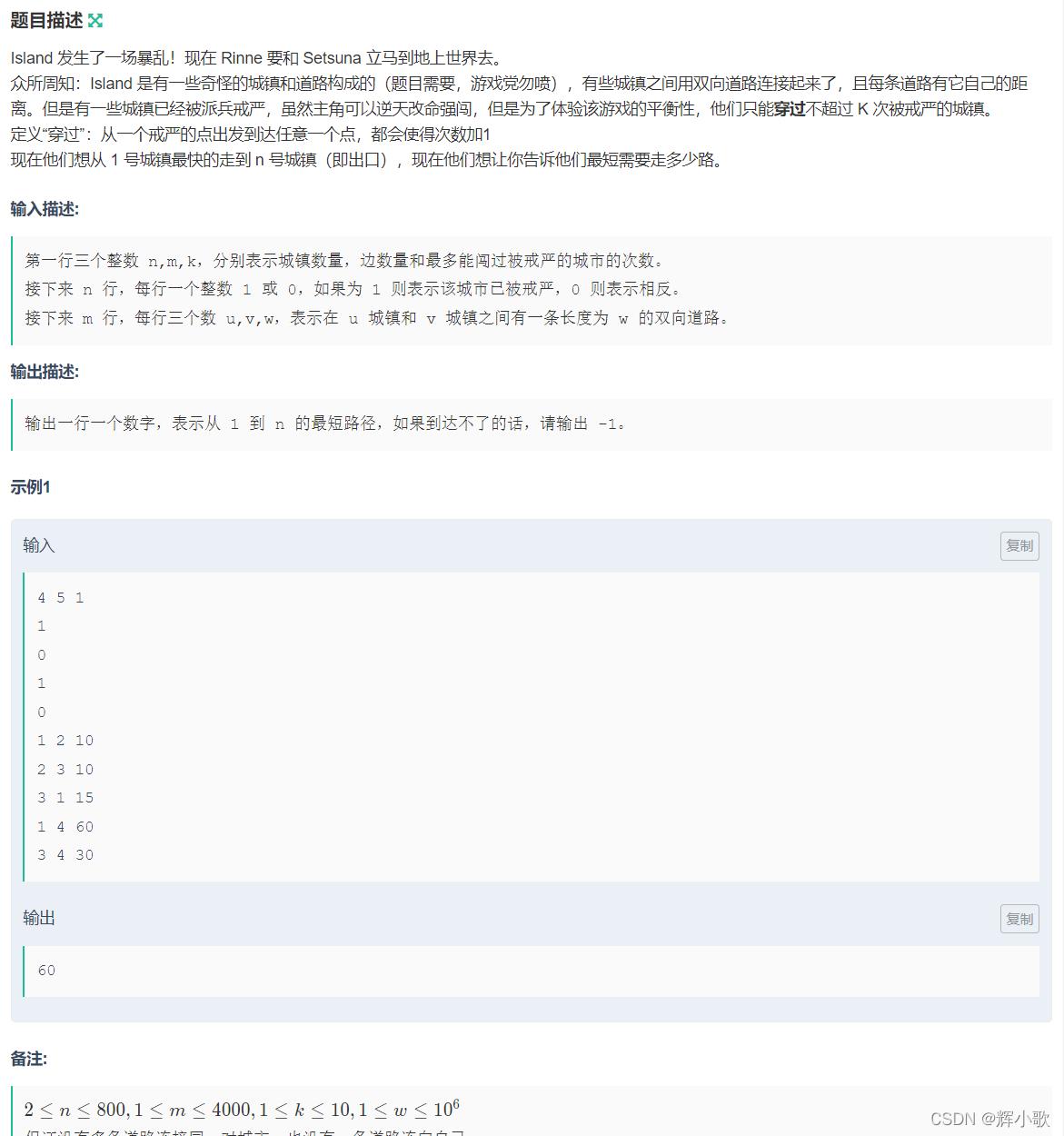
例如,这道题就是特殊的边不能走超过k次。

#include<bits/stdc++.h> 
using namespace std;
const int N=1e5*2+10;
typedef long long int LL;
int h[N],e[N],w[N],ne[N],idx;
LL dist[N][15],st[N][15];//dist[i][j] 表示i点距离1的最短距离，且走了j条特殊的边
int f[N],n,m,k;
void add(int a,int b,int c)

	e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;

struct node

	LL u,k,d;
	node(LL u,LL k,LL d): u(u), k(k), d(d) 
    friend bool operator < (node a, node b) 
        return a.d > b.d;//按照d小根堆
    
;
void Dijkstra(int s)

	memset(dist,0x3f,sizeof dist);
	priority_queue<node>q; q.push(s,0,0);
	dist[s][0]=0;
	while(q.size())
	
	    auto temp=q.top();  q.pop();
	    int u=temp.u,cnt=temp.k,d=temp.d;
	    if(st[u][cnt]) continue;
	    st[u][cnt]=1;
	    for(int i=h[u];i!=-1;i=ne[i])
	    
	        int j=e[i];
	        int tempk=cnt+f[u];
	        if(tempk>k) continue;//超过了k
	        if(!st[j][tempk]&&dist[j][tempk]>d+w[i])
	        
	            dist[j][tempk]=d+w[i];
	            q.push(j,tempk,dist[j][tempk]);
	        
	    
	

int main(void)

	memset(h,-1,sizeof h);
    cin>>n>>m>>k;
	for(int i=1;i<=n;i++) cin>>f[i];
	while(m--)
	
		int a,b,c; cin>>a>>b>>c;
		add(a,b,c),add(b,a,c);
	
	Dijkstra(1);
	LL ans=1e18;
	for(int i=0;i<=k;i++) ans=min(ans,dist[n][i]);
	cout<<ans;
	return 0;

例题二：

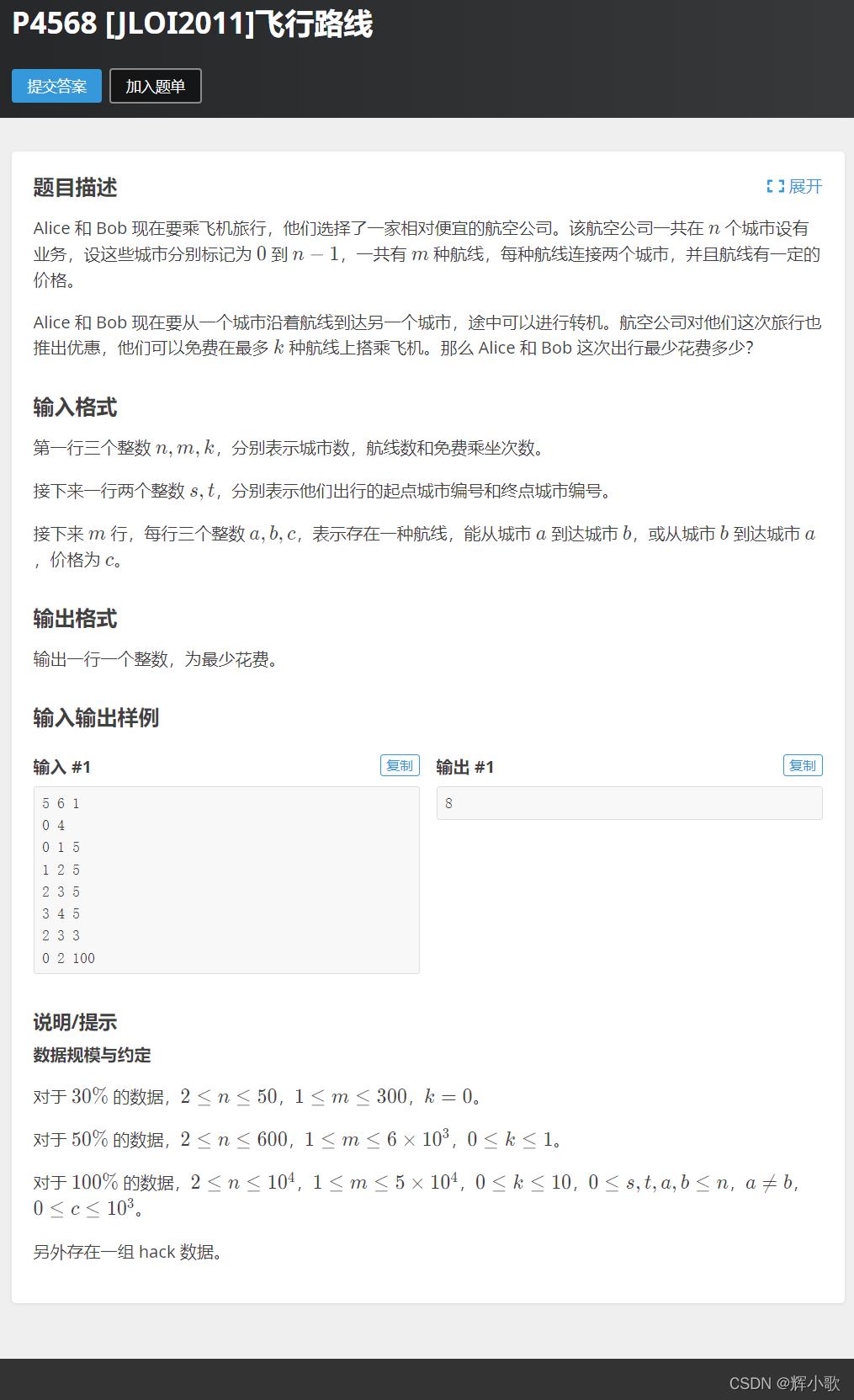
例如，这道就是选不超过k条边免费。

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
const int M=1e5+110;
typedef long long int LL;
int h[N],e[M],w[M],ne[M],idx;
int dist[N][15],st[N][15];
int n,m,k,bg,ed;
void add(int a,int b,int c)

	e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;

struct node

	LL u,k,d;
	node(LL u,LL k,LL d): u(u), k(k), d(d) 
    friend bool operator < (node a, node b) 
        return a.d > b.d;//按照d小根堆
    
;
void Dijkstra(int s)

	memset(dist,0x3f,sizeof dist);
	priority_queue<node>q; q.push(s,0,0);
	dist[s][0]=0;
	while(q.size())
	
	    auto temp=q.top();  q.pop();
	    int u=temp.u,cnt=temp.k,d=temp.d;
	    if(st[u][cnt]) continue;
	    st[u][cnt]=1;
	    for(int i=h[u];i!=-1;i=ne[i])
	    
	        int j=e[i];
	        if(dist[j][cnt]>dist[u][cnt]+w[i])//不免费
	        
	        	dist[j][cnt]=dist[u][cnt]+w[i];
				q.push(j,cnt,dist[j][cnt]);
	        
	        if(cnt+1<=k&&dist[j][cnt+1]>dist[u][cnt])//免费
	        
	        	dist[j][cnt+1]=dist[u][cnt];
				q.push(j,cnt+1,dist[j][cnt+1]);
	        
	    
	

int main(void)

	memset(h,-1,sizeof h);
	cin>>n>>m>>k;
	cin>>bg>>ed;
	while(m--)
	
		int a,b,c; cin>>a>>b>>c;
		add(a,b,c),add(b,a,c);
	
	Dijkstra(bg);
	int ans=1e9;
	for(int i=0;i<=k;i++) ans=min(ans,dist[ed][i]);
	cout<<ans;
	return 0;