蓝桥杯数论真题

Posted 2023-03-29 叁 柒

[蓝桥杯 2013 省 AB] 错误票据

题目背景

某涉密单位下发了某种票据，并要在年终全部收回。

题目描述

每张票据有唯一的 ID 号，全年所有票据的 ID 号是连续的，但 ID 的开始数码是随机选定的。因为工作人员疏忽，在录入 ID 号的时候发生了一处错误，造成了某个 ID 断号，另外一个 ID 重号。

你的任务是通过编程，找出断号的 ID 和重号的 ID。

数据保证断号不可能发生在最大和最小号。

输入格式

一个整数 $N(N<100)$ 表示后面数据行数，接着读入 $N$ 行数据，每行数据长度不等，是用空格分开的若干个（不大于 $100$ 个）正整数（不大于 $10^5$），每个整数代表一个 ID 号。

输出格式

要求程序首先输入要求程序输出 $1$ 行，含两个整数 $m$，$n$，用空格分隔，其中，$m$ 表示断号 ID，$n$ 表示重号 ID。

样例 #1

样例输入 #1

2
5 6 8 11 9
10 12 9

样例输出 #1

7 9

样例 #2

样例输入 #2

6
164 178 108 109 180 155 141 159 104 182 179 118 137 184 115 124 125 129 168 196
172 189 127 107 112 192 103 131 133 169 158
128 102 110 148 139 157 140 195 197
185 152 135 106 123 173 122 136 174 191 145 116 151 143 175 120 161 134 162 190
149 138 142 146 199 126 165 156 153 193 144 166 170 121 171 132 101 194 187 188
113 130 176 154 177 120 117 150 114 183 186 181 100 163 160 167 147 198 111 119

样例输出 #2

105 120

题目分析

这道题目要求找到的有两点，一种是重复的部分，一种是缺少的部分，先说重复的部分，这个比较简单，我们可以把所有数据都存储在一个数组中，将数组排序，然后遍历该数组，如果出现a[i]==a[i+1]就是重复的，也就是的就是重复数据了。我们只需要输出a[i]就可以啦。

再来看缺少的部分，既然缺少了，那肯定会导致排序后的数组不连贯，就一定存在相邻两项只差大于1的情况，我们只需要遍历数组，找到这个不连贯的地方，也就是a[i+1]-a[i]>1的地方，输出a[i]+1即可。

值得注意的是，这个题数据量还是比较大的，需要使用快读，否则可能会TLE。

完整代码

import java.io.*;
import java.util.*;
public class Main
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static PrintWriter pw=new PrintWriter(System.out);
    static int N = 100010;
    static int k,n,m,p;
    static int[] arr = new int[N];
    public static void main(String[] args)throws IOException
        k = Integer.parseInt(br.readLine());
        while(k --> 0)
            String[] s = br.readLine().split(" ");
            for(int i = 0;i <s.length;i++)
                arr[p++]=Integer.parseInt(s[i]);
            
        
        Arrays.sort(arr,0,p+1);
        for(int i = 0;i<p;i++)
            if(arr[i]==arr[i+1]) n = arr[i];
        
        for(int i = 0;i<p;i++)
            if(arr[i+1]-arr[i]>=2) m = arr[i]+1;
        
        System.out.println(m+" "+n);
    

[蓝桥杯 2014 省 AB] 蚂蚁感冒

题目描述

长 $100$ 厘米的细长直杆子上有 $n$ 只蚂蚁。它们的头有的朝左，有的朝右。

每只蚂蚁都只能沿着杆子向前爬，速度是 $1$ 厘米 / 秒。

当两只蚂蚁碰面时，它们会同时掉头往相反的方向爬行。

这些蚂蚁中，有 $1$ 只蚂蚁感冒了。并且在和其它蚂蚁碰面时，会把感冒传染给碰到的蚂蚁。

请你计算，当所有蚂蚁都爬离杆子时，有多少只蚂蚁患上了感冒。

输入格式

第一行输入一个整数 $n(1<n<50)$ 表示蚂蚁的总数。

接着的一行是 $n$ 个用空格分开的整数 $X_i(-100<X_i<100)$，$X_i$ 的绝对值，表示蚂蚁离开杆子左边端点的距离。正值表示头朝右，负值表示头朝左，数据中不会出现 $0$ 值，也不会出现两只蚂蚁占用同一位置。其中，第一个数据代表的蚂蚁感冒了。

输出格式

要求输出 $1$ 个整数，表示最后感冒蚂蚁的数目。

样例 #1

样例输入 #1

3
5 -2 8

样例输出 #1

1

样例 #2

样例输入 #2

5
-10 8 -20 12 25

样例输出 #2

3

分析

首先我们必须要明白两只蚂蚁相撞掉头可以看作时一只蚂蚁穿过了另一只蚂蚁，因为相撞之后两只蚂蚁都感冒了，掉不掉头其实无所谓，毕竟都感冒了，这样的话这题就简单多了。我们先不考虑特殊情况，先来看看一般情况：

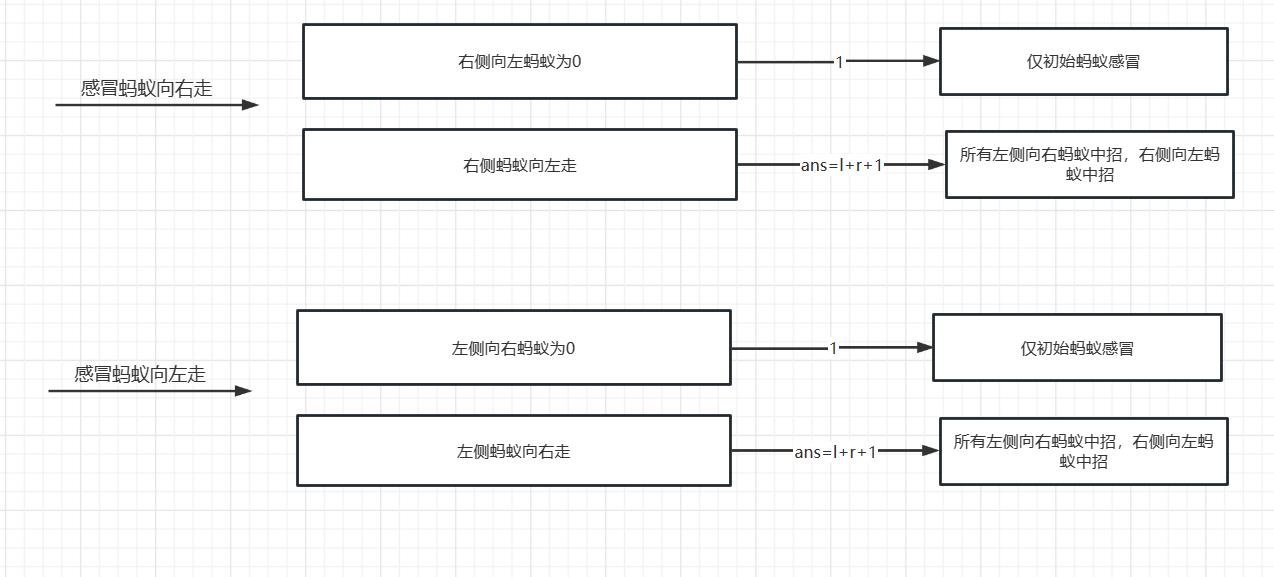
第一只蚂蚁不管方向朝哪里，只要它右边的蚂蚁向左走就可能碰撞感染，同样，第一只蚂蚁左边的蚂蚁只要朝右边走也可能被感染，这样就很容易得到ans=right+left+1
这里left表示左边蚂蚁向右走的数量，right表示右边蚂蚁向左走的数量，1是指第一只蚂蚁本身。

还有一种特殊情况，就是当第一只蚂蚁向左走的时候，如果第一只蚂蚁左边没有向右爬行的蚂蚁，由于爬行速度相同，所以不管第一只蚂蚁右边有多少向左爬行的，其右边的蚂蚁永远不可能被感染。同理，当第一只蚂蚁向右走的时候，如果第一只蚂蚁右边没有向左爬行的蚂蚁，其左边也永远不可能感染。

注意，我们需要记录的只有可能会相遇的蚂蚁，也就是前面分析中的在右向左和在左向右。

代码实现

import java.util.*;
public class Main
    static int N = 55;
    static int[] x = new int[N];
    public static void main(String[] args)
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        for(int i = 0;i < n;i++)
            x[i]=scan.nextInt();
        
        int l = 0,r = 0;//l是在左边向右走的蚂蚁，r是在右边向左走的蚂蚁
        for(int i = 0;i<n;i++)
             if(Math.abs(x[i])<Math.abs(x[0])&&x[i]>0) l++;
             if(Math.abs(x[i])>Math.abs(x[0])&&x[i]<0) r++;
        
        if(x[0]>0 && r>0 || x[0]<0 && l>0) System.out.println(l+r+1);
        else System.out.println(1);
    

蓝桥杯每日一真题—— [蓝桥杯 2021 省 AB2] 完全平方数（数论，质因数分解）

文章目录

• [蓝桥杯 2021 省 AB2] 完全平方数
• • 题目描述
  • 输入格式
  • 输出格式
  • 样例 #1
  • • 样例输入 #1
    • 样例输出 #1
  • 样例 #2
  • • 样例输入 #2
    • 样例输出 #2
  • 提示
  • • 思路：
    • • 理论补充：完全平方数的一个性质：完全平方数的质因子的指数一定为偶数
      • 最终思路：
      • 小插曲：
    • 全部代码

[蓝桥杯 2021 省 AB2] 完全平方数

题目描述

一个整数 $a$ 是一个完全平方数，是指它是某一个整数的平方，即存在一个 整数 $b$，使得 $a=b^2$ 。

给定一个正整数 $n$，请找到最小的正整数 $x$，使得它们的乘积是一个完全平方数。

输入格式

输入一行包含一个正整数 $n$。

输出格式

输出找到的最小的正整数 $x$。

样例 #1

样例输入 #1

12

样例输出 #1

3

样例 #2

样例输入 #2

15

样例输出 #2

15

提示

对于 $30\%$ 的评测用例, $1\le n\le 1000$，答案不超过 $1000$。

对于 $60\%$ 的评测用例，$1\le n\le 10^8$，答案不超过 $10^8$。

对于所有评测用例，$1\le n\le 10^{12}$，答案不超过 $10^{12}$。

蓝桥杯 2021 第二轮省赛 A 组 G 题（B 组 H 题）。

思路：

这一看直接暴力就只能得一点点分，我还数论学的不太好先暴力得了30分。然后开始想办法吧！
没办法。。。看答案吧。。。

理论补充：完全平方数的一个性质：完全平方数的质因子的指数一定为偶数

1.唯一分解定理任意一个数 n，它都可以分解为若干个质数的乘积。

2.需要知道完全平方数的一个性质：完全平方数的质因子的指数一定为偶数。附上大佬的证明过
程：

最终思路：

对n进行质因数分解，如果质因数的指数为奇数的话就在x中乘以这个质因子这样，可以让指数保持偶数，如果是偶数那就不用管它~~~~
1.分解质因子：

for (long long i = 2; i * i <= n; i++)
    
        if (n % i == 0)
        
            cnt++;//记录有多少个因子，后面好遍历
        

        while (n % i == 0)
        
            a[cnt] = i;//a数组存因子
            g[cnt]++;//g数组存因子指数
            n = n / i;
        
    

    if (n > 1)
    
        a[++cnt] = n;
        g[cnt]++;
    //考虑没分解完的情况

2,根据性质得出答案：

  for (int i = 1; i <= cnt; i++)//遍历如果有奇数就让原来的n*ans*这个奇数质因子也就是让ans*这个奇数质因子
    
        if (g[i] % 2)
        
            ans = ans * a[i];
        
    
    cout << ans;

小插曲：

质因数分解写错了最后输出了和n一样的数竟然得了60分！！

全部代码

#include <iostream>
using namespace std;

long long n, ans = 1, g[1000], a[1000], cnt;
int main()

    cin >> n;
    // 首先对n进行质因数分解
    for (long long i = 2; i * i <= n; i++)
    
        if (n % i == 0)
        
            cnt++;//记录有多少个因子，后面好遍历
        

        while (n % i == 0)
        
            a[cnt] = i;//a数组存因子
            g[cnt]++;//g数组存因子指数
            n = n / i;
        
    

    if (n > 1)
    
        a[++cnt] = n;
        g[cnt]++;
    //考虑没分解完的情况
    //完全平方数的质因子的指数一定为偶数
    for (int i = 1; i <= cnt; i++)//遍历如果有奇数就让原来的n*ans*这个奇数质因子也就是让ans*这个奇数质因子
    
        if (g[i] % 2)
        
            ans = ans * a[i];
        
    
    cout << ans;
    system("pause");
    return 0;