利用CPU的分支预测(Branch Prediction)模型优化if-else
Posted 星空_MAX
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了利用CPU的分支预测(Branch Prediction)模型优化if-else相关的知识,希望对你有一定的参考价值。
现代计算机和编译器的结构更加智能化,会想尽办法去把CPU所有部件全部利用起来,不想让CPU的任何区域出现空闲
我前面的文章提到过simd优化,将CPU的数据位宽利用起来,CPU累加器在单个时钟周期里并行完成数据位宽/数据类型大小的计算,对32位操作系统而言,32位的宽度能放下4个float类型的数据,也就能一次完成一个四维向量的累加计算,大大利用了总线的宽度
下面将介绍另一种能“压榨”计算机性能的优化手段
分支预测
分支预测(Branch Prediction)是从Pentium5代开始的一种先进的,解决处理分支指令(if-then-else)导致流水线失败的数据处理方法,由CPU来判断程序分支的进行方向,能够加快运算速度。
先看个程序
写一个程序,产生32768个从0到256的随机数,然后依次判断是否大于128,如果大于则累计
重复这个过程100000次,将最后的时间统计出来
首先是没有排序的数组:
#include <algorithm>
#include <ctime>
#include <iostream>
#define ARRAYSIZE 32768
int main()
// 产生数组
int data[ARRAYSIZE] ;
// 将数组1到1024之间的随机数填充
for (int i = 0; i < ARRAYSIZE; ++i)
data[i] = std::rand() % 256;
//排序函数,一会将比较它开没有开启的时间
//std::sort(data, data + ARRAYSIZE);
//记录开始时间
clock_t start_time = clock();
//循环求和
long long sum = 0;
//将主要计算部分执行100000次,减少误差
for (int i = 0; i < 100000; ++i)
// 主要计算部分,选大于128的数字累加,即中间大小的数字
for (int j = 0; j < ARRAYSIZE; ++j)
if (data[j] >= 128)
sum += data[j];
//记录结束时间
clock_t end_time = clock();
//计算出累加部分花费的时间
double ElapsedTime = static_cast<double>(end_time - start_time) / CLOCKS_PER_SEC;
//打印累加时间
std::cout << "ElapsedTime:" << ElapsedTime << std::endl;
注意,排序注释掉了
//std::sort(data, data + ARRAYSIZE);运行结果:
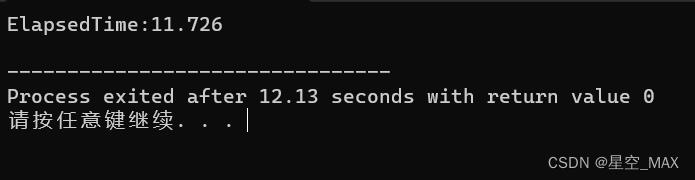
将排序打开:
std::sort(data, data + ARRAYSIZE);运行结果:
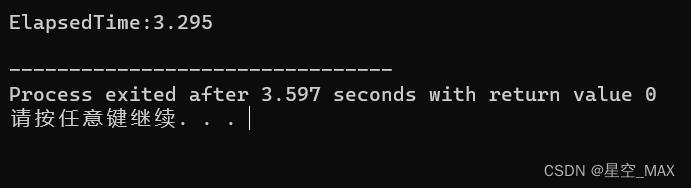
可见对随机数组排序前和排序后的结果性能差距大于三倍
在java下的运行结果
import java.util.Arrays;
import java.util.Random;
public class Main
public static void main(String[] args)
int ArraySize = 32768;
// 产生数组
int data[] = new int[ArraySize];
// 将数组1到1024之间的随机数填充
Random rnd = new Random(0);
for (int i = 0; i < ArraySize; ++i)
data[i] = rnd.nextInt() % 256;
//排序函数,一会将比较它开没有开启的时间
//Arrays.sort(data);
//记录开始时间
long start_time = System.nanoTime();
//循环求和
long sum = 0;
//将主要计算部分执行100000次,减少误差
for (int i = 0; i < 100000; ++i)
// 主要计算部分,选大于128的数字累加,即中间大小的数字
for (int j = 0; j < ArraySize; ++j)
if (data[j] >= 128)
sum += data[j];
//记录结束时间
long end_time = System.nanoTime();
//计算出累加时间
System.out.println("ElapsedTime:"+(end_time - start_time) / 1000000000.0);
在有没有开启Arrays.sort(data)的条件下
Arrays.sort(data);结果为:
没有开启排序

开启排序后

性能差距也在三倍以上
而且java比C++的运行的效率更高,可能做了其他优化,这里以后再找原因
对于data[j] >= 128
每回判断的时候需要暂停下来,等程序进入后面,那面积是不是可以预先判定它每回结果,然后就可以跳过这一个步骤,实际上程序就是这么做的,下面将展开介绍这种原因出现的原因
关于CPU流水线
cpu流水线技术是一种将指令分解为多步,并让不同指令的各步操作重叠,从而实现几条指令并行处理,以加速程序运行过程的技术。 指令的每步有各自独立的电路来处理,每完成一步,就进到下一步,而前一步则处理后续指令。
对于CPU的管线里面,存在以下四个步骤:
- 读取指令(Fetch)
- 指令解码(Decode)
- 运行指令(Execute)
- 回写(Write-back)
对于一条指令会分别在四个区域执行,那么如果要等一条指令执行的时候,才开始执行后一条指令的,那么就会有三个区域是空闲的
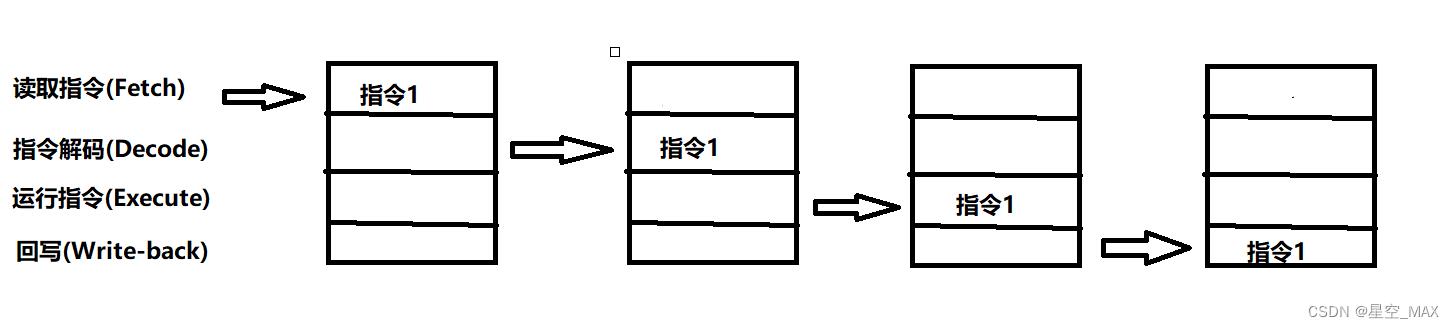
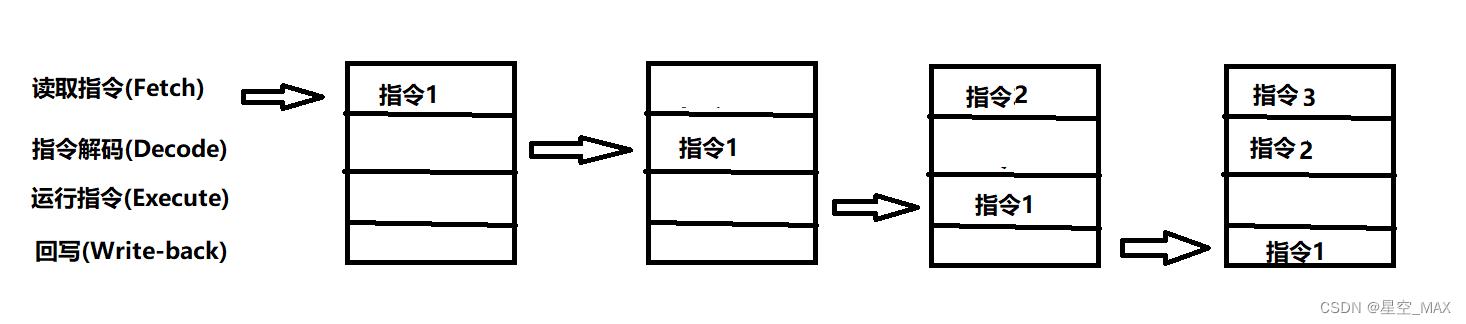
那么可不可以在第一条指令进行到后面步骤的时候,再载入后面的指令那,答案是可以的,那么就会变成下图所示:

那么一条流水线就会同时运行四条指令
但是,条件跳转指令,只要当前面的指令运行到执行阶段,才能知道要选择的分支
当遇到判断的时候,就会造成流水线冒泡(bubbling),造成流水线利用率降低
分支预测
结合上面的问题,那么就可以提前预测结果,然后让流水线保持运载运行,然后同时判断预测结果是否正确
如果预测正确,那就继续执行
如果预测失败,那就冲刷流水线,重新获取指令、译码
那么对于下面程序来说
// 主要计算部分,选大于128的数字累加,即中间大小的数字
for (int j = 0; j < ARRAYSIZE; ++j)
if (data[j] >= 128)
sum += data[j];
给分支走向给下面两个标记
T = 分支命中
N = 分支没有命中
如果分支排序过,就会有下面的branch:
data[] = 226, 185, 125, 158, 198, 144, 217, 79, 202, 118, 14, 150, 177, 182, 133, ...
branch = T, T, N, T, T, T, T, N, T, N, N, T, T, T, N ...完全不可预测
如果数组没有排序过,就会有下面的branch:
data[] = 0, 1, 2, 3, 4, ... 126, 127, 128, 129, 130, ... 250, 251, 252, ...
branch = N N N N N ... N N T T T ... T T T ...前面全是false,后面全是true
很显然就可以预测了
可预测就可以跳过条件跳转指令,从而提高了流水线的占用率,程序就会快了
如何避免分支预测提高程序的运行效率呢
我这里先提供 两个方案:
利用表查询:
如果事先对数组排序消耗很大,这里用到了表查询的技巧
int lookup[256];
for (int i = 0; i < 256; ++i)
lookup[i] = (i >= 128) ? i : 0;
构造一张表,将不符合的位置记录为为0,符合的数字记为自己本身
for (unsigned i = 0; i < ARRAY_SIZE; ++i)
sum += lookup[data[i]];
累加的时候,没有判断,只不过不符合的数字全部加为0,这样就避免了分支判断
利用位运算取消分支跳转:
通过data[i] - 128计算出正负值
(data[i] - 128)>>31右移31位,若小于128得到-1,大于等于128得到0
-1转换为二进制为0xffff,0为0x0000
用~反转一下
若为正确的数字和0xffff与一下,则是原来的数字
若不正确和0x0000与一下,就是0了
for (unsigned i = 0; i < ARRAY_SIZE; ++i)
int t = (data[i] - 128) >> 31;
sum += ~t & data[i];
分支预测分类
分支预测技术包含编译时进行的静态分支预测和硬件在执行时进行的动态分支预测
最简单的静态分支预测方法就是任选一条分支。这样平均命中率为50%,更精确的办法是根据原先运行的结果进行统计从而尝试预测分支是否会跳转
动态分支预测是近来的处理器已经尝试采用的的技术。最简单的动态分支预测策略是分支预测缓冲区(Branch Prediction Buff)或分支历史表(branch history table)
下面介绍两种预测分类
1-bit动态预测
根据该指令上次是否跳转来预测此次是否跳转。如果上次跳转,则预测此次也会跳转
对于上面排好的数组简直是太适用了,这个预测只在开始和中间部分会改变两次,剩下就不会发生分支预测失效了
2-bit动态预测
这种预测又称为双模态预测器或者饱和预测器

分为00 01 10 11四种状态
当处于00和01状态时候预测为采纳分支
当处于10和11状态时候预测为不采纳分支
当预测为采纳的时候向左推一个状态,如果为00态则保持不变
当预测为不采纳分支的时候向左推一个状态,如果为11态则保持不变
该条件分支指令必须连续选择某条分支两次,才能从强状态翻转,从而改变了预测的分支
适合一直稳定突然出现变化的抢矿
两级自适应预测器:
简单来说就是可以记录周期性的跳转,能预测一个模式
分两个部分,前面是一个分支历史寄存器,后面跟了一个饱和预测器
对于001001001001的情况而言
拿一个2-bit自适应预测器来说,前面历史记录器发现00,然后跳转到后面的饱和预测器,就能马上判断是1的可能性大了

根据饱和寄存器A中的状态机状态,下一个为1的可能性能极大 ,这就是大致原理
下面是一张4-bit的自适应器
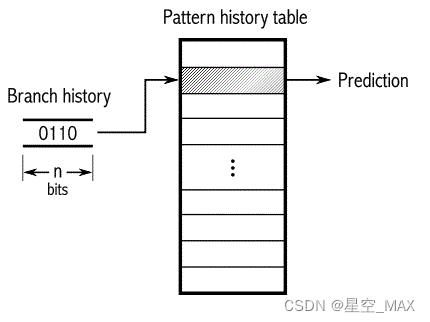
分支历史表更大了,其他原理一样
对于n-bit的BHR而言,可以准确追踪重复周期在n以内的分支历史pattern。如果程序中某个分支历史的pattern周期超过n,性能就会受到影响
当然还有其他分支预测器,这里就不展开介绍了
CPU微架构设计利用Verilog设计基于饱和计数器和BTB的分支预测器
在基于流水线(pipeline)的微处理器中,分支预测单元(Branch Predictor Unit)是一个重要的功能部件,它负责收集和分析分支/跳转指令的参数和执行结果,当处理新的分支/跳转指令时,BPU将根据已有的统计结果和当前分支跳转指令的参数,预测其执行结果,为流水线取指提供决策依据,进而提高流水线效率。
下面讨论提出分支预测机制的主要原因和实际意义:
在流水线处理分支跳转指令时,目标地址往往需要推迟到指令的执行阶段才能运算得出,在此之前处理器无法及时得知下一条指令的取指地址,因此无法继续取指。一种解决方法是在识别分支指令后,令取指流水级及相关的流水级暂停(stall),等待分支目标地址计算完成后再继续取指。这将浪费若干流水线时钟周期,从而降低性能。采用这种方法的流水线暂停效果示意图如下:
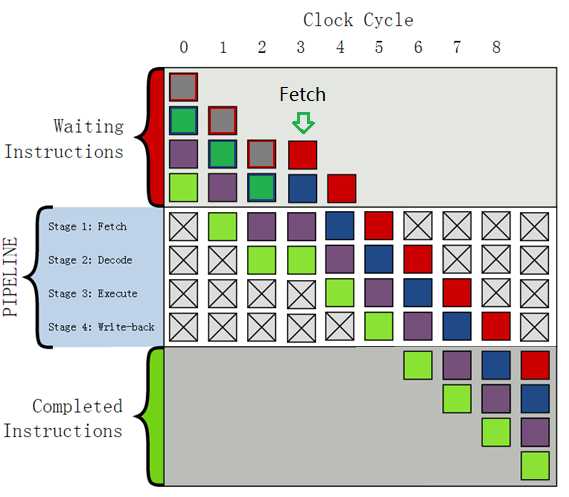
(附图:经典的四级流水线中分支指令引发的流水线暂停示意图,坐上紫色方块代表分支指令。由于采用简单的理想流水线,分支指令目标地址在执行阶段即可得出,这将浪费一个流水线时钟周期)
为改进以上方法, 我们考虑引进一种静态分支预测机制,即预测分支跳转指令一定不跳转(not taken),则上述情况将成为:默认分支跳转指令之后的指令也流入pipeline,在若干流水级后,分支指令的地址将被计算得出,此时才判断之前流入流水线的指令是否为实际目标地址所指向的指令,若真,流水线可以继续运行而不必暂停;但若假,则之前流入的指令都无效,相关流水级将被冲刷(flush),处理器只能重新从正确的地址开始取值,这将同样降低流水线的效率。
可以看到,采用静态预测后,在处理分支/跳转指令时,流水线在一定概率下将不会因分支而暂停,这就降低了出现流水线气泡周期的可能性。然而,在对性能要求较高的场合,此方法仍旧不能令人满意。
为进一步提高效率,我们考虑动态分支预测机制。动态预测基于对分支历史的记录统计,预测出分支跳转的“方向”和“目标地址”。若处理器按照预测结果取指,则一旦预测结果与实际跳转结果相同,之前流入流水线的指令将完全有效,流水线将维持运行。处理器按照预测出的“方向”和“目标地址”进行取值的行为称为预测取值(Speculative Fetch),执行按照预测结果取出的指令的行为称为预测执行(Speculative Execution)
随着预测算法的不断改进,当前分支预测的准确率不断向1逼近,分支预测技术有效提高了流水线的运行效率,被大量运用到主流微处理器中。
一、分支预测需要解决的问题
(1)、预测分支是否发生,即预测“方向”的问题;
(2)、预测分支指令设置的取值地址,即预测“目标地址”的问题。
二、分支预测单元的设计实现
常见的分支预测机制主要可分为一级结构和两级结构。对于两级预测器,常见的算法包括gshare和gselect算法,这种算法考虑到分支指令的上下文执行历史,精度相对较高,但实现相对复杂,本文不予讨论。对于一级预测器,其设计是将多个饱和计数器和BPU组织成一维向量表,利用分支/跳转指令PC值的hash映射值寻址一维向量表。这种预测器结构最为简单,本文将针对这种结构做详细的讨论。
2.1 分支方向的预测
本文采用2bit的饱和计数器,用于寄存4种状态。根据预测结果和实际执行结果,计数器的值将按照如下所示状态机转移图转移。
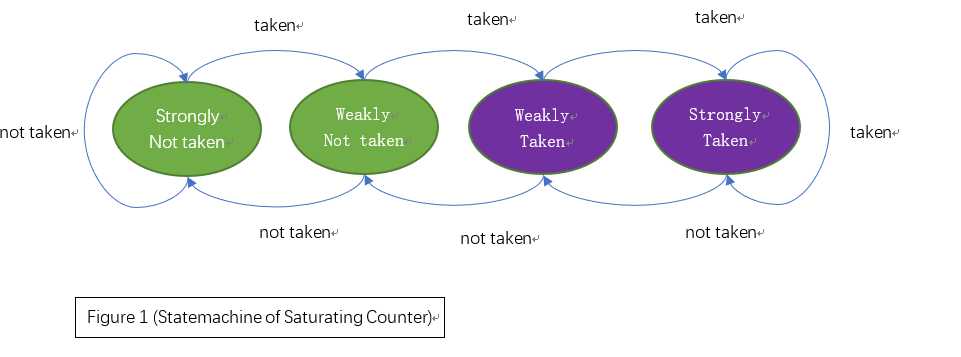
图中跳转(taken)和不跳转(not taken)两种状态分别被进一步细分为强(strong)和弱(weak)共四种状态,并规定strongly taken和weakly taken为“跳转”、strongly not taken和weakly not taken为“不跳转”,且每当预测出错后,计数器会以相反方向更改状态,这种做法的本质其实是一种“阻尼式”的切换。
2.2 分支目标地址的预测
为了简化设计,本文主要讨论基于分支目标缓存(Branch Target Buffer)技术的预测器。BTB使用容量有限的缓存寄存最近执行的分支指令的目标地址。对于后续分支指令,预测时直接取出对应表项中寄存的地址作为目标地址预测值。当分支指令被执行后,将实际的目标地址回写入BTB中,为下次预测提供依据。
本设计中,使用使用分支指令PC值的hash映射值寻址BTB表项,使得每条分支跳转指令都能与BTB表项建立起映射关系。
其中,我们定义PC值的hash映射规则如下:
∫ V(PC) → V(hash), f(p) , f(p) = p & 1111111111b (即取出PC值的低10位作为对应的hash映射值)
2.3 设计总体框架
综上所述,分支预测器的总体结构如下,可以看出,该预测器具有极其简单的结构:
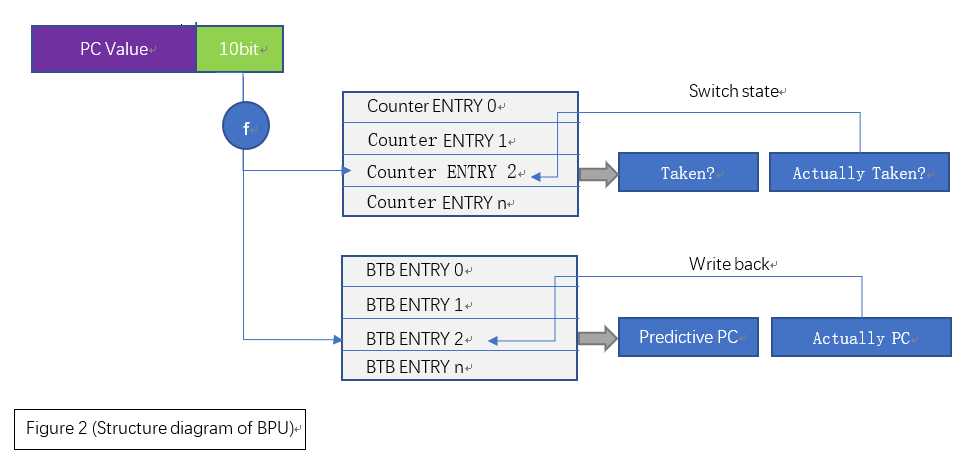
三、硬件描述语言实现
通过以上讨论,容易使用Verilog HDL实现分支预测器。
值得注意的是,这里仅对饱和计数器进行非溢出的递增或递减,利用计数值的最高位判断是否发生跳转,1为taken,0为not taken。
1 module bpu 2 #( 3 parameter PCW = 30, // The width of valid PC 4 parameter BTBW = 10, // The width of btb address 5 ) 6 (/*AUTOARG*/ 7 // Outputs 8 pre_taken_o, pre_target_o, 9 // Inputs 10 clk, rst_n, pc_i, set_i, set_pc_i, set_taken_i, set_target_i 11 ); 12 13 // Ports 14 input clk; 15 input rst_n; 16 input [PCW-1:0] pc_i; // PC of current branch instruction 17 input set_i; 18 input [PCW-1:0] set_pc_i; 19 input set_taken_i; 20 input [PCW-1:0] set_target_i; 21 output reg pre_taken_o; 22 output reg [PCW-1:0] pre_target_o; 23 24 // Local Parameters 25 localparam SCS_STRONGLY_TAKEN = 2‘b11; 26 localparam SCS_WEAKLY_TAKEN = 2‘b10; 27 localparam SCS_WEAKLY_NOT_TAKEN = 2‘b01; 28 localparam SCS_STRONGLY_NOT_TAKEN = 2‘b00; 29 30 wire bypass; 31 wire [BTBW-1:0] tb_entry; 32 wire [BTBW-1:0] set_tb_entry; 33 34 // PC Address hash mapping 35 assign tb_entry = pc_i[BTBW-1:0]; 36 assign set_tb_entry = set_pc_i[BTBW-1:0]; 37 assign bypass = set_i && set_pc_i == pc_i; 38 39 // Saturating counters 40 reg [1:0] counter[(1<<BTBW)-1:0]; 41 generate begin :counter 42 integer entry; 43 always @(posedge clk or negedge rst_n) 44 if(!rst_n) 45 for(entry=0; entry < (1<<BTBW); entry=entry+1) // reset BTB entries 46 counter[entry] <= 2‘b00; 47 else if(set_i && set_taken_i && counter[set_tb_entry] != SCS_STRONGLY_TAKEN) begin 48 counter[set_tb_entry] <= counter[set_tb_entry] + 2‘b01; 49 else if(set_i && !set_taken_i && counter[set_tb_entry] != SCS_STRONGLY_NOT_TAKEN) begin 50 counter[set_tb_entry] <= counter[set_tb_entry] - 2‘b01; 51 end 52 endgenerate 53 54 always @(posedge clk) 55 pre_taken_o <= bypass ? set_taken_i : counter[tb_entry][1]; 56 57 // BTB vectors 58 reg [PCW-1:0] btb[(1<<BTBW)-1:0]; 59 60 generate begin :btb_rst 61 integer entry; 62 always @(posedge clk or negedge rst_n) 63 if(!rst_n) 64 for(entry=0; entry < (1<<BTBW); entry=entry+1) begin // reset BTB entries 65 btb[entry] <= {PCW{1‘b0}}; 66 end 67 endgenerate 68 69 always @(posedge clk) 70 pre_target_o <= bypass ? set_pc_i : btb[tb_entry]; 71 72 always @(posedge clk) 73 if( set_i ) 74 btb[set_tb_entry] <= set_target_i; 75 76 endmodule
对该实现需要做如下说明:
(1)、BPU在每个时钟周期内完成预测和更新。pc_i端口输入待预测的指令PC值,set_i端口指示是否在下一个时钟周期到来时更新预测器。
(2)、考虑到特殊的指令流情况,该实现添加了旁路(bypass)机制。对于具体的处理器实现,可能永远不会触发旁路,因此可以去掉这部分实现。
(3)、对于在BTB中没有记录的分支指令,BPU默认预测目标地址输出为0(BTB在此之前进行过置零复位)。对于具体的处理器实现,可考虑将分支指令的下一条指令的PC值作为目标地址的预测值。
四、总结
通过讨论,我们提出了基于饱和计数器和BTB的分支预测单元的设计思路,并最终利用Verilog实现了该分支预测器的原型。该实现在面积上具有一定优势,可运用于微处理器实验和验证等方面;同时,该设计也存在一些不足之处:
(1)、在求PC值的hash映射值时,仅简单地取PC低10bit的数据作为BTB的索引,这将导致PC值高位相同的分支指令的记录状态互相混淆,从而降低预测精度;
(2)、该设计仅考虑分支指令的全局状态,而没有跟踪分支指令具体的上下文环境;
(3)、对于带条件判断的分支指令、或寄存器直接/间接寻址的跳转指令,由于其操作数保存在寄存器中,而寄存器的值往往是不断变化的,这将导致对分支目标地址的预测精度降低。
===================================================
本博文仅供参考,难免有错误或疏漏之处,欢迎提出宝贵意见。
以上是关于利用CPU的分支预测(Branch Prediction)模型优化if-else的主要内容,如果未能解决你的问题,请参考以下文章