K-Means 聚类算法 Python实现
Posted 叫我小陈就好
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了K-Means 聚类算法 Python实现相关的知识,希望对你有一定的参考价值。
聚类算法
将物理或抽象对象的集合分成由类似的对象组成的多个类的过程被称为聚类。由聚类所生成的簇是一组数据对象的集合,这些对象与同一个簇中的对象彼此相似,与其他簇中的对象相异。“物以类聚,人以群分”,在自然科学和社会科学中,存在着大量的分类问题。聚类分析又称群分析,它是研究(样品或指标)分类问题的一种统计分析方法。聚类分析起源于分类学,但是聚类不等于分类。聚类与分类的不同在于,聚类所要求划分的类是未知的。聚类分析内容非常丰富,有系统聚类法、有序样品聚类法、动态聚类法、模糊聚类法、图论聚类法、聚类预报法等。
(以上名词解释源自百度百科)
K-Means基本思想
- 初始化中心点
- 计算样本点与中心点之间的距离,将样本点归为最近的中心点的类中
- 根据类划分,计算新的样本中心点
- 重复操作直到中心点或类的归属不再发生变化
需要预设类的个数为K
代码解析
生成随机样本
import torch
import math
import matplotlib.pyplot as plt
# 利用torch的函数生成随机的样本点
X=torch.randn(2000)*100
y=torch.randn(2000)*100
# 一个长度为2000的向量,表示点的类别归属
C=torch.zeros(2000)生成初始中心点
# 设置k-means的类别数
K = 5
CentPoint = []
for i in range(K):
CentPoint.append([torch.randint(-100,100,(1,)).item(),
torch.randint(-100,100,(1,)).item()])K-Means算法
# 计算二维平面上点的距离
def dis(a,b):
return math.sqrt((a[0]-b[0])*(a[0]-b[0])+(a[1]-b[1])*(a[1]-b[1]))
# K-Means
# 一般执行10次以内即可完成分类
for p in range(10):
# NewPoint初始化为0
NewPoint = [[0, 0] for i in range(K)]
for i in range(len(X)):
mDis=1e9
mC=0
for j in range(len(CentPoint)):
cp=CentPoint[j]
D = dis([X[i].item(), y[i].item()], cp)
# print("distance:", D)
if mDis>D:
mDis=D
mC=j
C[i]=mC
# print("mC",mC,C[i].item())
NewPoint[mC][0]+=X[i].item()
NewPoint[mC][1]+=y[i].item()
# 更新中心点
for i in range(K):
CentPoint[i][0]=NewPoint[i][0]/2000
CentPoint[i][1]=NewPoint[i][1]/2000
# 输出中心点,观察变化过程
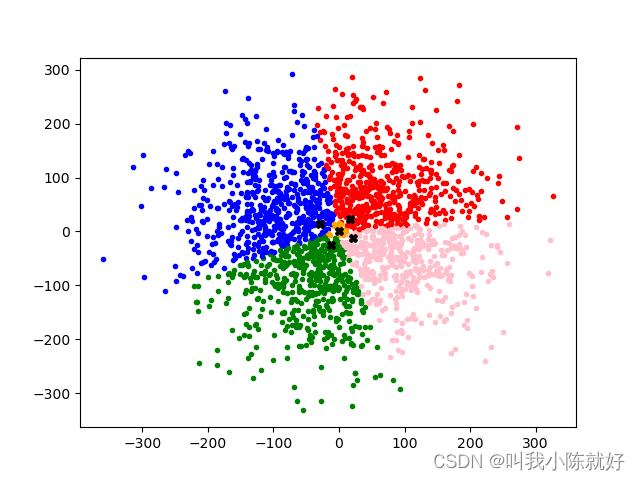
print(CentPoint)结果展示
cc=list(C)
# 按不同颜色来区分不同种类的点
for i in range(len(X)):
if cc[i]==0:
plt.plot(X[i].item(), y[i].item(), 'r.')
elif cc[i]==1:
plt.plot(X[i].item(), y[i].item(), 'g.')
elif cc[i]==2:
plt.plot(X[i].item(), y[i].item(), 'b.')
elif cc[i]==3:
plt.plot(X[i].item(), y[i].item(), color='pink', marker='.')
elif cc[i]==4:
plt.plot(X[i].item(), y[i].item(), color='orange', marker='.')
# 样本聚类的中心点
for CP in CentPoint:
plt.plot(CP[0], CP[1], color='black', marker='X')可以观察出来,由于这组随机样本的生成是基于二维正态分布的,用K-Means来分析聚类,五个中心点的位置十分接近于二维正态分布的中心。
完整代码
import torch
import math
import matplotlib.pyplot as plt
def dis(a,b):
return math.sqrt((a[0]-b[0])*(a[0]-b[0])+(a[1]-b[1])*(a[1]-b[1]))
X=torch.randn(2000)*100
y=torch.randn(2000)*100
C=torch.zeros(2000)
K = 5
CentPoint = []
for i in range(K):
CentPoint.append([torch.randint(-100,100,(1,)).item(),
torch.randint(-100,100,(1,)).item()])
print(CentPoint)
for p in range(10):
NewPoint = [[0, 0] for i in range(K)]
for i in range(len(X)):
mDis=1e9
mC=0
for j in range(len(CentPoint)):
cp=CentPoint[j]
D = dis([X[i].item(), y[i].item()], cp)
if mDis>D:
mDis=D
mC=j
C[i]=mC
NewPoint[mC][0]+=X[i].item()
NewPoint[mC][1]+=y[i].item()
for i in range(K):
CentPoint[i][0]=NewPoint[i][0]/2000
CentPoint[i][1]=NewPoint[i][1]/2000
print(CentPoint)
cc=list(C)
for i in range(len(X)):
if cc[i]==0:
plt.plot(X[i].item(), y[i].item(), 'r.')
elif cc[i]==1:
plt.plot(X[i].item(), y[i].item(), 'g.')
elif cc[i]==2:
plt.plot(X[i].item(), y[i].item(), 'b.')
elif cc[i]==3:
plt.plot(X[i].item(), y[i].item(), color='pink', marker='.')
elif cc[i]==4:
plt.plot(X[i].item(), y[i].item(), color='orange', marker='.')
for CP in CentPoint:
plt.plot(CP[0], CP[1], color='black', marker='X')
plt.show()K-Means聚类算法与Python实现
在数据挖掘中,K-Means算法从一个目标集中创建多个组,每个组的成员都是比较相似的。这是个想要探索一个数据集时比较流行的聚类分析技术,也可以说是一种最简单的聚类算法了。
算法实现过程:
k-means 算法的工作过程说明如下:
首先从含n个数据对象的数据集中任意选择k个对象作为初始聚类中心;
对于所剩下其它对象,则根据它们与这些聚类中心的相似度,分别将它们分配给与其最相似的(聚类中心所代表的)聚类;
然后再计算每个所获新聚类的聚类中心(该聚类中所有对象的均值);
不断重复这一过程直到标准测度函数开始收敛为止。
一般都采用均方差作为标准测度函数。
k个聚类有以下特点:各聚类本身尽可能的紧凑,而各聚类之间尽可能的分开。
伪代码说明表示流程如下:
选择k个点作为起始质心(一般随机选择) 当任意一个点的簇分配结果发生改变时 对数据集中的每个数据点 对每个质心 计算质心与数据点之间的距离 将数据点分配到距其最近的簇 对每一个簇,计算簇中所有点的均值并将均值作为质心 |
算法优缺点:
优点:容易实现,最大好处就是这个了
缺点:
1)k值的选择是用户指定的,不同的k得到的结果会有挺大的不同
2)对k个初始质心的选择比较敏感,容易陷入局部最小值
3)存在局限性,非球状数据分布可能就搞不定了
4)数据较大时,效率较低,收敛速度慢
算法实现和设计:
代码实现如下
import numpy as np |
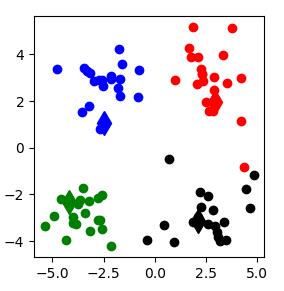
运行效果截图:(每次结果可能存在不同)
1.
2:
3:
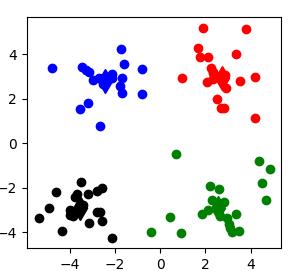
4:
5:
对于如何提高聚类效果,这就是另一个话题啦,我们后面再讨论。
以上是关于K-Means 聚类算法 Python实现的主要内容,如果未能解决你的问题,请参考以下文章