432统计简答（个人笔记）

Posted 2022-04-17 是璇子鸭

简答题/面试题属开放性问答，答案并不唯一，因此自己对问题的理解与阐述就显得尤为重要。除说准基本概念外，适当具体加以论证更有助于表达。
以下为方便个人记忆而整理的部分简答及解析，仅供参考，欢迎读者斧正或在评论区补充。

统计学

统计学是一门研究如何收集、组织、分析和解释数据，利用数据做出决策的科学。与数学不同，数学的证明是基于公理和假设的，证明的过程依赖的是演绎推理，得到的结论是必然成立的。而统计学强调的是数据产生的背景，根据背景寻找合适的抽象方法和推断方法，推理的过程依赖的是归纳推理，得到的结论是或然成立的。

贝叶斯分类

贝叶斯分类利用统计学中的贝叶斯定理，来预测类成员的概率，即给定一个样本，计算该样本属于一个特定的类的概率。（应用：利用贝叶斯分类器减少诊断费用）

聚类分析

定义：是研究“物以类聚”的一种多元统计方法。它未预先指定类别，将一个给定数据对象集合分成不同的簇（cu），属于无监督分类法。

其常规应用主要有：模式识别、空间数据分析（根据地质断层的特点把已观察到的地震中心分成不同的类）、经济学（尤其是市场研究方面，如帮助市场人员发现客户中的不同群体，然后用这些知识来开展一个目标明确的市场计划）

一个好的聚类方法要能产生高质量的聚类结果——簇，这些簇要具备以下两个特点：

• 高的簇内相似性
• 低的簇间相似性

因此，聚类结果的好坏取决于该聚类方法采用的相似性评估方法以及该方法的具体实现

聚类分析可通过样本个体或指标变量进行分类，分为Q型（样本聚类分析）和R型（指标聚类分析）两类。

前者目的在于将分类不明确的样本按性质相似程度分成若干组，从而发现同类样本的共性和不同类样本间的差异；
后者目的是将分类不明确的指标按性质相似程度分成若干组，从而在尽量不损失信息的条件下，用一组少量的指标来代替原来的多个指标

其次，聚类分析也不同于因素分析和判别分析：因素分析是根据所有变量间的相关关系提取公共因子；聚类分析是先将最相似的两个变量聚为一小类，再去与最相似的变量或小类合并，如此分层依次进行；
而判别分析是要先知道各种类，然后判断某个案是否属于某一类

综上概括，聚类分析的结果取决于变量的选择和变量值获取的两个方面。变量选择越准确、测量越可靠，得到的分类结果越是能描述事物各类间的本质区别。

再者，聚类分析完全是根据数据情况来进行的。就一个由n个样本、k个特征变量组成的数据文件来说 ，当对样本进行聚类分析时，相当于对k 维坐标系中的n 个点进行分组，所依据的是它们的距离 ；当对变量进行聚类分析时，相当于对n维坐标系中的k个点进行分组，所依据的也是点距。所以距离或相似性程度是聚类分析的基础。点距如何计算呢？拿连续测量的变量来说，可以用欧氏距离平方计算：即各变量差值的平方和。注意聚类分析前要检查各变量的量纲是否一致，不一致则需进行转换，如将各变量均作标准化转换就可保证量纲一致。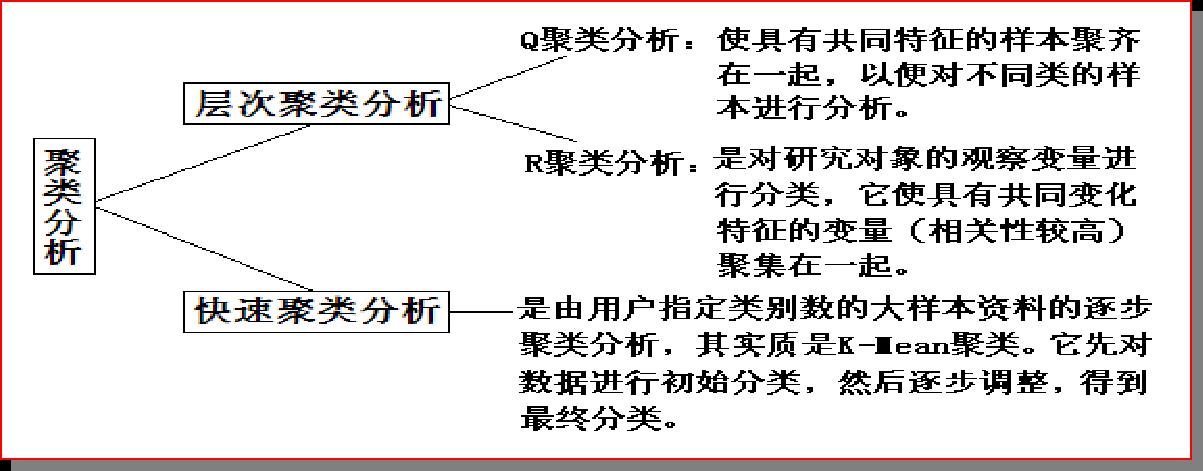

判别分析

判别分析又称“分辨法”，是在分类确定的条件下，根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。

实际生活中，判别分析也被广泛用于预测判断事物的类别归属。企业营销中，营销人员可通过已有的客户特征数据（如消费金额、消费频次、购物时长、购买产品种类等），预测当前的消费者属于哪种类型的顾客（款式偏好型、偏重质量型、价格敏感型…），并根据其特点有针对性的采取有效的营销手段；或是根据各成分含量指标，判断白酒的品牌或水果的产地等。

中心极限定理

设从均值为u，方差为σ^2 的一个任意总体中抽取容量为n的样本，当n充分大时，样本均值的抽样分布近似服从均值为u，方差为σ^2/n的正态分布。

抽样误差

（1）抽样误差是由于抽样的随机性所带来的误差；
（2）所有可能样本的统计结果与总体真实值之间的平均性差异；
（3）通常是可以计算和控制的；

影响抽样误差大小的因素主要有：
1、样本容量的大小
2、总体的变异程度
3、抽样方式和方法

点估计与区间估计

点估计：用样本统计量直接作为总体参数估计值的抽样推断方法。
如：用样本均值直接作为总体均值的估计值（但该方法没有给出估计值接近总体参数程度的信息）。
常见方法：矩估计法、最大似然法、最小二乘法等
区间估计：在点估计的基础上，给出总体参数估计的一个区间范围，该区间是由样本统计量加减抽样误差而得到的。
根据样本统计量的抽样分布，能够对样本统计量与总体参数的接近程度给出一个概率度量。

假设检验

先对总体的参数（或分布形式）提出某种假设，然后利用样本信息判断假设是否成立的统计推断过程。
有参数检验和非参数检验两类方法
在逻辑上运用反证法，统计上依据小概率事件

其基本步骤为：

假设检验中的两类错误：

假设检验中的小概率原理：
（1）小概率是指在一次试验中，一个几乎不可能发生的事件发生的概率；
（2）在一次试验中小概率事件一旦发生，我们就有足够的理由拒绝原假设；
（3）小概率由研究者事先确定

异方差的检验与修正

之所以讨论异方差是因为在回归分析和方差分析中都是假设样本之间是同方差的。方差分析的同方差是指各组之间的方差相等；回归分析中的同方差则指对于每一个样本点来说，随机误差的平方和是一样的。

而异方差就是说不同样本点间受随机误差的影响不同，即随机误差平方和不一样。（其后果、诊断方法、补救措施详见链接）

相关分析与回归分析

区别：
联系：
（1）都是对变量间相关关系的分析；
（2）只有当变量间存在相关分析时，用回归分析去寻求相关的具体数学形式才有实际意义；
（3）相关分析只表明变量间相关关系的性质和程度，要确定相关的具体数学形式依赖于回归分析；
（4）相关分析中相关系数的确定，建立在回归分析的基础上；

个人认为（2）（3）（4）是同一个意思；
相关系数r描述的是线性相关关系，并不等价于相关本身

直线相关关系的特点：

拟合优度R^2

解释变量对被解释变量的解释比例

方差分析

基本思想：通过对数据误差来源的分析来判断不同总体的均值是否相等，进而分析自变量对因变量是否有显著影响

三个基本假定：
①每个总体应服从正态分布（对于因素的每一个水平，其观测值是来自正态分布的简单随机样本）；
②各个总体的方差必须相同（对于各组观察数据，其是从具有相同方差的正态总体中抽取的）；
③观测值独立。

多重共线性

什么是多重共线性？(DW)
在进行回归分析时，自变量之间彼此相关的现象，就成为多重共线性。

适度的多重共线性不成问题，但当出现严重共线性问题时，会导致分析结果不稳定，出现回归系数的符号与实际情况完全相反的情况。本应该显著的自变量不显著，本不显著的自变量却呈现出显著性，这种情况下就需要消除多重共线性的影响

出现的原因
1、自变量间线性关系较强
2、数据不足。（在某些情况下，收集更多数据可解决共线性问题）
3、错误地使用虚拟变量（比如同时将男、女两个虚拟变量都放入模型，此时必出现完全共线性）

判别指标
（1）回归分析中的VIF方差膨胀因子，其值越大，多重共线性越严重。一般认为VIF大于10即表示模型存在严重的共线性问题。
（2）容差值（1/VIF）
（3）直接对自变量进行相关分析，查看相关系数和显著性也是一种判别方法。如果一个自变量和其他自变量间的相关系数显著，则代表可能存在多重共线性问题。

如何处理：
多重共线性是普遍存在的，在VIF<5时，不需要做特别的处理。若多重共线性问题较为严重，可考虑使用一下几种方法处理：
1、手动移除共线性变量（最直接）；
2、逐步回归法
3、增加样本容量（在时间和成本允许的条件下）；
4、岭回归

注：存在多重共线性的模型在用于预测时，往往不影响预测结果

关于抽样

一个好的抽样设计必须同时考虑到精度与费用两个方面

样本估计的评价标准：
1、无偏性:估计量抽样分布的数学期望等于被估计的总体参数；
2、有效性：对同一总体参数的两个无偏点估计量，标准差更小的更有效；
3、一致性：随着样本容量的增大，估计量的值越来越接近被估计的总体参数。

时间序列的构成因素：

①长期趋势：即时间序列在长时间内呈现出来的某种持续向上或持续下降的变动，可以是线性的，也可以是非线性的；
②季节性：一年内重复出现的周期性波动，“季节”一词是广义的，不单指一年中的四季，也包括任何一种周期性变化；
③周期性：围绕长期趋势的一种波浪形或振荡式变动；
④随机性：时间序列中除去趋势、周期性和季节性之后的偶然性波动。

标准正态随机变量的平方和服从卡方分布？

该说法并不正确。当标准正态随机变量间不相互独立，其平方和不服从卡方分布。

t分布与标准正态分布的联系与区别

思路：谈谈两个最基本的抽样分布，可以从构造、分布性质、假设检验来谈

从分布上看：
区别：t分布依赖于自由度，相较于标准正态分布尾部更厚，分布曲线比较低平；而标准正态分布图像受位置参数u和离散程度σ的影响；

联系：t分布由标准正态分布以及卡方分布构造而成。（可以具体说一下如何构造，要强调标准正态和卡方独立）；
同时，t分布自由度越大，越接近标准正态分布，当n趋于无穷时，t分布就会变成一个标准正态分布；

从假设检验：
在构造检验统计量时，一般而言，如果已知构造z统计量，如果未知，构造t统计量。

在大数据时代的今天，统计学发展面临的机遇和挑战

谈谈统计学与机器学习的关系以及前景