备战数学建模5-数据统计分析多项式计算

Posted 2022-04-17 nuist__NJUPT

目录

一、数据统计分析

1-求矩阵或向量的最大值与最小值

2-求矩阵的平均值或中值

3-求和和求积

4-标准差与相关系数

5-排序

二、多项式计算

1-多项式的表示

2-多项式的四则运算

3-多项式的求导

4-多项式的求值

 5-多项式的求根

---

一、数据统计分析

1-求矩阵或向量的最大值与最小值

max()函数用于求向量或矩阵的最大元素，min()函数用于 求向量或矩阵的最小元素。

当参数是向量时，含有有两种调用格式：

y = max(x) 表示返回向量x的最大元素存入y，若x中有复数，则取模的最大值存入y。

[y,k] = max(x) 表示返回向量x的最大值存入y，并存入相应的序号k。

我们看一下上面的例子1，求出向量x中的最大值。

x = [-43, 72, 9, 16, 23, 47] ;
y = max(x) ; %求向量的最大值 
y
[y,k] = max(x) ; %求向量的最大值和对应的序号
[y,k]

当参数A是矩阵的时候，函数有三种调用格式

max(A)表示返回一个行向量，向量的第i个元素是矩阵第i列的最大值。

[Y,U] = max(A)表示返回向量Y和U，Y向量记录A的每列的最大值，U记录每列最大元素的行号。

max(A,[],dim)函数：当dim等于1时，与max(A)用法一样，当dim等于2时，返回一个列向量，表示第i个元素是A矩阵第i行的最大值。

我们看一下上面的例子2，求出矩阵行列最大元素和整个矩阵的最大元素。

代码如下所示：

A = [13,-56,78; 25,63,-235; 78,25,563; 1,0,-1] ;
max(A) %返回一个行向量，表示每一列的最大值
max(A') %返回一个行向量，表示每一行的最大值
max(A,[],2)%返回一个列向量，表示每一行的最大值
max(max(A)) %返回矩阵的最大值

2-求矩阵的平均值或中值

平均值：元素和除以元素个数，中值：元素个数为奇数，取中间值，元素个数为偶数，取中间两个值的平均值。

mean()函数用于求平均值，median()函数用于求中值。

我们对x求平均值，得到1900，求中值为1200，由于个不饿同学生活费过高，导致均值过高，所以此处选择中值作为生活额度更合理。 

x = [1200, 800, 1500, 1000, 5000] ;
mean(x) 
median(x)

3-求和和求积

sum()函数是矩阵或向量的求和函数，prod(）函数是矩阵或向量的求积函数。

cumsum()函数求累加和，cumprod()函数求累乘积。

 我们看一下上面的例子4，代码如下所示，其中积是一个标量，累乘积是一个向量，向量中的每个值都是之前元素的累乘值。代码如下所示：

x = [1,2,3,4,5,6,7,8,9,10] ;
y1 = prod(x)
y2 = cumprod(x) 

4-标准差与相关系数

标准差用于计算数据偏离平均数的距离的平均值，std()函数计算标准差。

标准差的计算公式如下所示：s1为样本标准差，s2为总体标准差

调用格式：

（1）std(x)：计算向量x的标准差。

（2)  std(A):计算矩阵各列的标准差。

（3）std(A,flag,dim):flag取0或1，当flag取0，按s1所列公式计算样本标准差，flag=1时，按s2总体公式计算总体标准差。默认情况下，flag等于0，dim等于1.

我们看一下上面的例子5，具体的代码如下所示：

 x = randn(50000,4) ;
 y1 = std(x,0,1) %按公式s1求样本标准差
 y2 = std(x,1,1) %按公式s2求总体标准差

%下面的写法也是可以的
x = randn(50000,4) ;
x1 = x' ;
y3 = std(x1,0,2);
y3'
y4 = std(x1,1,2);
y4'

 相关系数：能够反映两组序列之间的相互关系，其值越是接近于0，说明序列相关度越低，其值的绝对值越接近于1，说明序列的相关度越高。相关系数的计算公式如下：

corrcoef()函数计算相关系数。

该函数的调用方式如下：

corrcoef(A):返回矩阵A形成的一个相关系数矩阵，其中第i行第j列的元素表示原矩阵A中第i行第j列的相关系数。

corrcoef(X,Y):在这里，X,Y是向量，它们与这个crrcoef([X,Y])一样，用于求向量X,Y的相关系数。

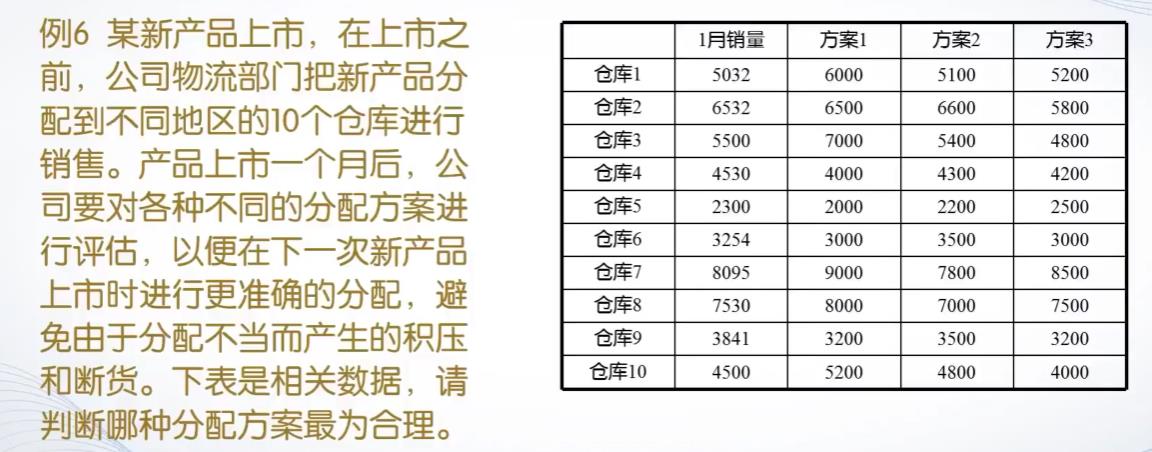
我们看一下例子6，1月销量和各个方案的相关系数，判断哪个方案最为合理，相关系数的绝对值越接近于1，说明相关性越强，最适合选择。

代码如下，求出的第一列与后面3列的相关系数分别为0.9630    0.9906    0.9782，故选择方案2最合理。

 A = [5032, 6000, 5100, 5200;
6531, 6500, 6600, 5800;
5500, 7000, 5400, 4800;
4530, 4000, 4300, 4200;
2300, 2000, 2200, 2500;
3254, 3000, 3500, 3000;
8095, 9000, 7800, 8500;
7530, 8000, 7000, 7500;
3841, 3200, 3500, 3200;
4500, 5200, 4800, 4000];
corrcoef(A)

5-排序

MATLAB中的排序函数sort().

排序函数的调用个数如下：

sort(X):对向量X按照升序进行排序。

[Y,I] = sort(A, dim, model):其中，dim指明对A的列还是行进行排序，model设置按照升序还是降序排序，默认升序，若取‘ascend’,则按升序，若取'descend'则按照降序排序。Y代表排序后的矩阵，I记录了Y中的元素在A中的位置。

我们看一下上面的例子7，对矩阵A进行各种排序。

A = [1, -8, 5; 4, 12, 6; 13, 7, -13] ;
sort(A) %对A的每一列进行升序排序
sort(A, 2, 'descend') %对A的每一行进行降序排序
[X,I] = sort(A) %对矩阵A进行升序排序，X是排序后的结果，I记录元素在A中的位置

二、多项式计算

1-多项式的表示

在MATLAB中，n次的多项式用长度为n+1的行向量表示，如下所示：

 

在MATLAB中创建多项式向量时候，需要注意三点：

第一，多项式系数向量的顺序是从高到底。

第二，多项式系数向量包含0次项系数，所以其长度为多项式最高次加1。

第三，如果有的项没有，系数向量位置应该用0补充。

2-多项式的四则运算

1-多项式的加减运算，就是相应向量的相加减。

2-多项式乘法，使用多项式乘法函数conv(p1,p2),其中p1和p2是两个多项式系数向量。

3-多项式除法，[Q,r] = deconv(p1,p2),其中Q是多项式p1除以p2的商式，r是p1除以p2的余式，Q环和r仍是多项式的系数向量。

我们可以发现deconv()函数是conv()函数的逆函数，故我们可以得到如下等式：

p1 = conv(p2,Q) + r ;

我们通过上面的例子1，看一下多项式的四则运算，代码如下所示：

f = [3, -5, 0, -7, 5, 6] ;
g = [3, 5, -3] ;
g1 = [0, 0, 0, g] ;
f + g1
f - g1
conv(f,g)
[Q, r] = deconv(f, g)

3-多项式的求导

在MATLAB中我们使用polyder()函数进行求导。

该函数的调用个数有如下几种：

p = polyder(P)表示求多项式P的导数。

p = polyder(P,Q)表示求P.Q的导函数。

[p,q] = polyder(P,Q)表示求P/Q的导函数，导函数的分子存入p，分母存入q。

我们看一下上面的例子2，求多项式乘积和商的导函数，代码如下所示：
 

a = [3, 1, 0, -6] ;
b = [1,2];
d = conv(a,b) ; %求两个多项式之积
c = polyder(d) %求导函数
c = polyder(a,b) %直接求两个多项式之积的导函数
[p,q] = polyder(a,b) %求多项式相除的导函数，导数的分子存入p，分母存入q

4-多项式的求值

MATLAB中使用polyval(p,x)函数进行代数多项式求值，使用polyvalm(p,x)进行矩阵多项式求值。

 

我们看一下上面的例子2，具体的代码如下所示：

a = [1, 8, 0, 0, -10] ;
x = [-1, 1.2; 2, 1.8] ;
y1 = polyval(a,x)
y2 = polyvalm(a,x)

 5-多项式的求根

MATLAB中使用roots(p)函数求多项式p的根，其中p为多项式的系数向量。

看一下上面的例子，代码如下所示：

a = [1, 8, 0, 0, -10] ;
roots(a)

 若已知多项式的全部根，可以用poly函数建立其多项式，调用格式为p = poly(x),x为根，p为系数向量。

我们看一下例子4这个优化问题，其实就算找多项式在区间内的极值点，代码如下：

p = [-38.89, 126.11, -3.42] ; %构建多项式系数向量
q = polyder(p) ; %求导数
r = roots(q) %求导数等于0时候的根
ans = polyval(p,r) %根据极值点求极值
x = 0 : 0.1 : 2 ;
plot(x, polyval(p,x),r,ans,'rp')
set(gca, 'xTick', 0:0.2:2) ;
hold on ;
y = -20 : 2 : ans ;
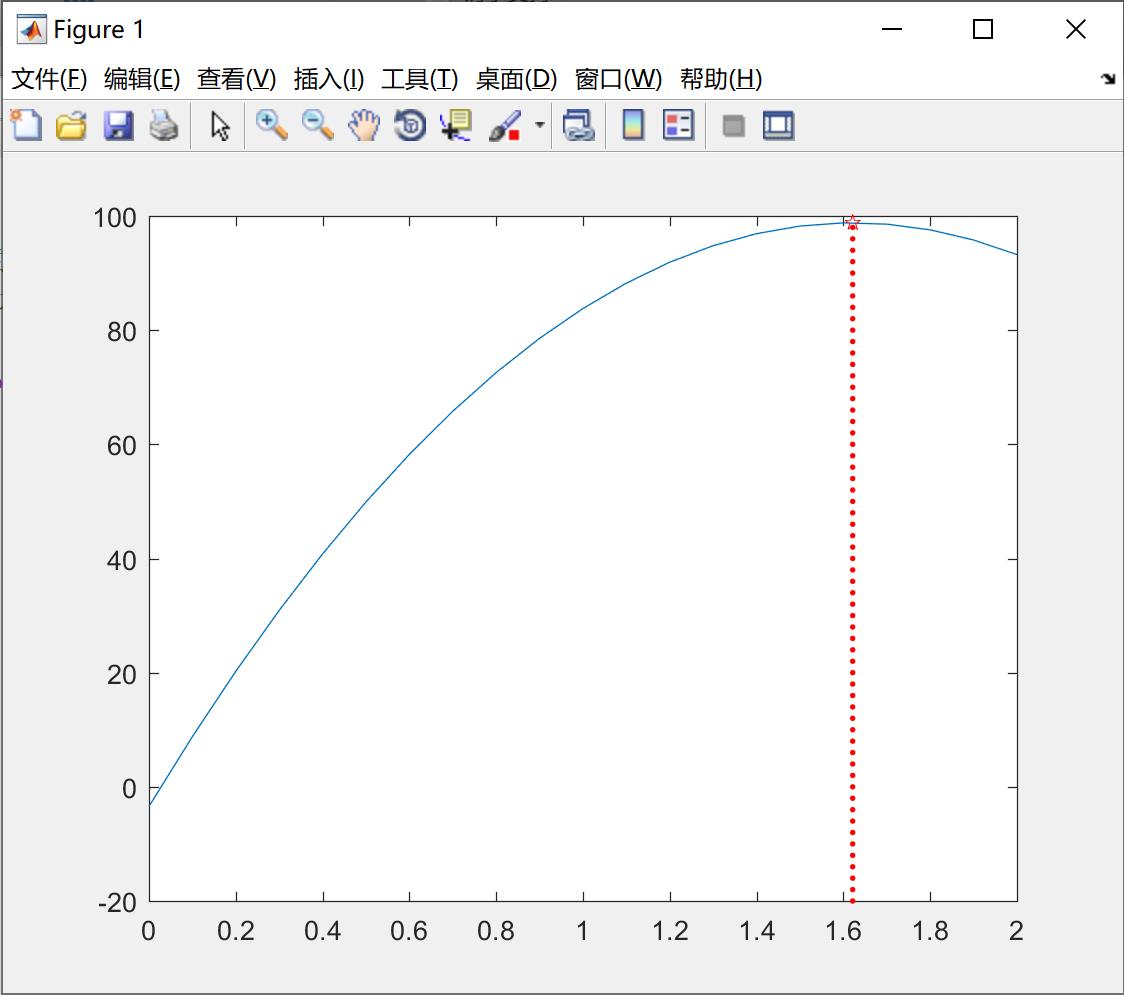
plot(x1,y,'r.')

绘制的图形如下所示，我们可以发现，当x= 1.6214时，加热效率p(x)最高，最高为 98.8154.